The Principle of Uncertain Maximum Entropy

The principle of maximum entropy, as introduced by Jaynes in information theory, has contributed to advancements in various domains such as Statistical Mechanics, Machine Learning, and Ecology. Its resultant solutions have served as a catalyst, facilitating researchers in mapping their empirical observations to the acquisition of unbiased models, whilst deepening the understanding of complex systems and phenomena. However, when we consider situations in which the model elements are not directly observable, such as when noise or ocular occlusion is present, possibilities arise for which standard maximum entropy approaches may fail, as they are unable to match feature constraints. Here we show the Principle of Uncertain Maximum Entropy as a method that both encodes all available information in spite of arbitrarily noisy observations while surpassing the accuracy of some ad-hoc methods. Additionally, we utilize the output of a black-box machine learning model as input into an uncertain maximum entropy model, resulting in a novel approach for scenarios where the observation function is unavailable. Previous remedies either relaxed feature constraints when accounting for observation error, given well-characterized errors such as zero-mean Gaussian, or chose to simply select the most likely model element given an observation. We anticipate our principle finding broad applications in diverse fields due to generalizing the traditional maximum entropy method with the ability to utilize uncertain observations.

IRL with Partial Observations using the Principle of Uncertain Maximum Entropy

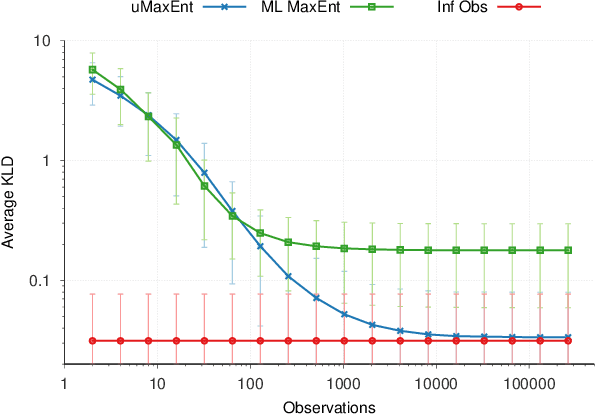
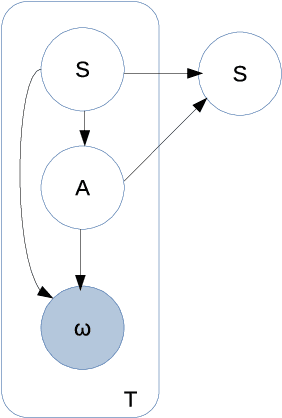
The principle of maximum entropy is a broadly applicable technique for computing a distribution with the least amount of information possible while constrained to match empirically estimated feature expectations. However, in many real-world applications that use noisy sensors computing the feature expectations may be challenging due to partial observation of the relevant model variables. For example, a robot performing apprenticeship learning may lose sight of the agent it is learning from due to environmental occlusion. We show that in generalizing the principle of maximum entropy to these types of scenarios we unavoidably introduce a dependency on the learned model to the empirical feature expectations. We introduce the principle of uncertain maximum entropy and present an expectation-maximization based solution generalized from the principle of latent maximum entropy. Finally, we experimentally demonstrate the improved robustness to noisy data offered by our technique in a maximum causal entropy inverse reinforcement learning domain.

Notes on Generalizing the Maximum Entropy Principle to Uncertain Data

The principle of maximum entropy is a broadly applicable technique for computing a distribution with the least amount of information possible while commonly constrained to match empirically estimated feature expectations. We seek to generalize this principle to scenarios where the empirical feature expectations cannot be computed because the model variables are only partially observed, which introduces a dependency on the learned model. Extending and generalizing the principle of latent maximum entropy, we introduce uncertain maximum entropy and describe an expectation-maximization based solution to approximately solve these problems. We show that our technique generalizes the principle of maximum entropy and latent maximum entropy and discuss a generally applicable regularization technique for adding error terms to feature expectation constraints in the event of limited data.

A Hierarchical Bayesian model for Inverse RL in Partially-Controlled Environments

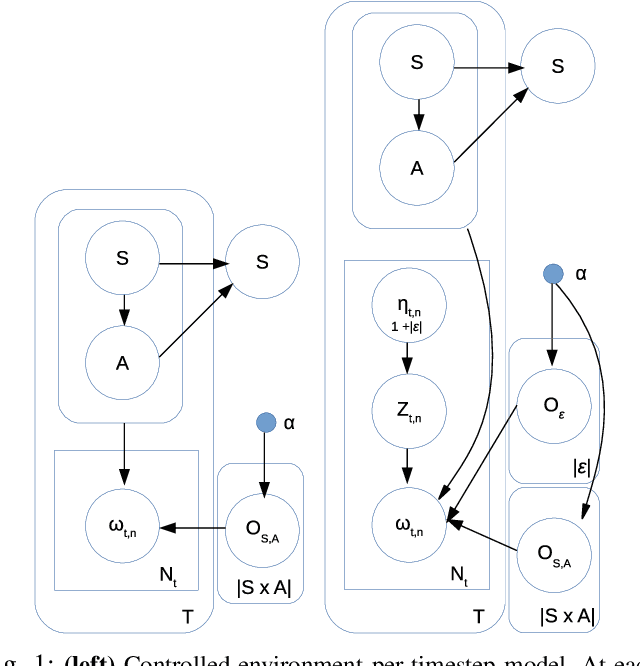
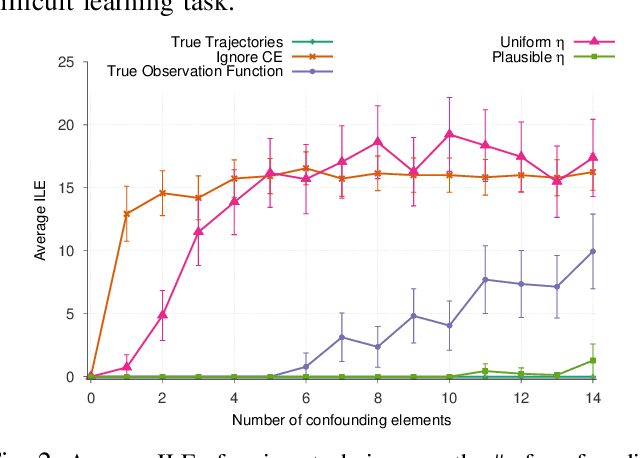
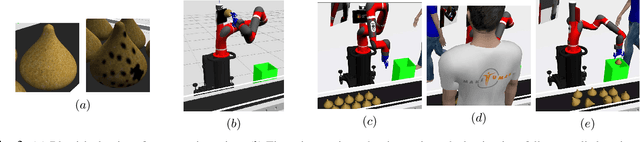
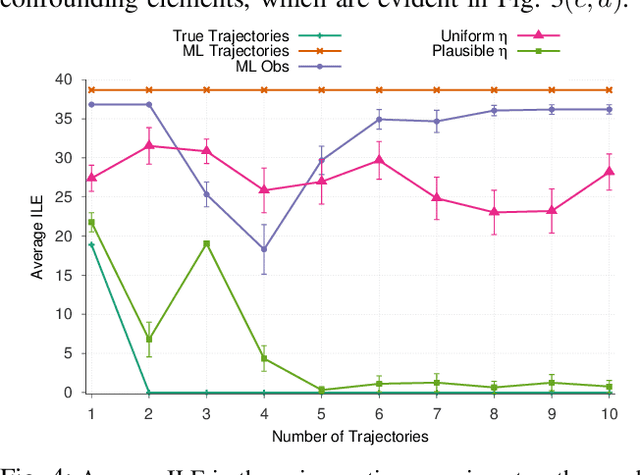
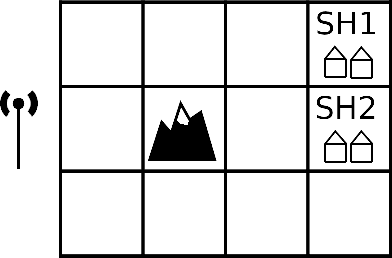
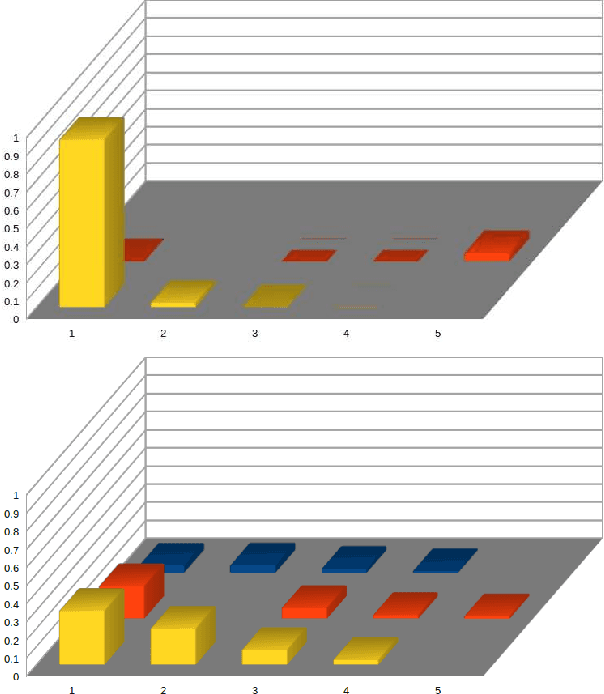
Robots learning from observations in the real world using inverse reinforcement learning (IRL) may encounter objects or agents in the environment, other than the expert, that cause nuisance observations during the demonstration. These confounding elements are typically removed in fully-controlled environments such as virtual simulations or lab settings. When complete removal is impossible the nuisance observations must be filtered out. However, identifying the source of observations when large amounts of observations are made is difficult. To address this, we present a hierarchical Bayesian model that incorporates both the expert's and the confounding elements' observations thereby explicitly modeling the diverse observations a robot may receive. We extend an existing IRL algorithm originally designed to work under partial occlusion of the expert to consider the diverse observations. In a simulated robotic sorting domain containing both occlusion and confounding elements, we demonstrate the model's effectiveness. In particular, our technique outperforms several other comparative methods, second only to having perfect knowledge of the subject's trajectory.