Keanu Sisouk
Robust Barycenters of Persistence Diagrams
Sep 18, 2025
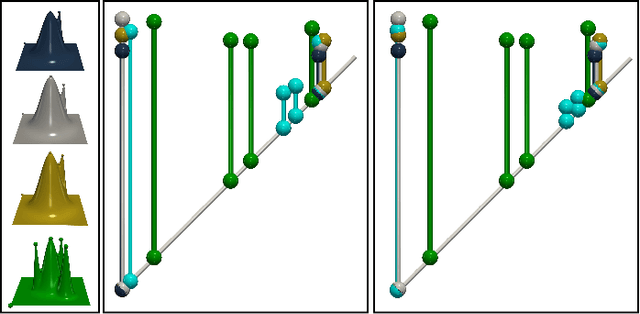
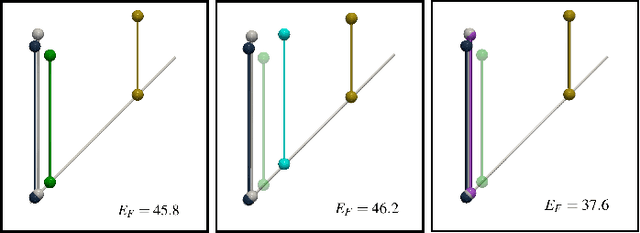
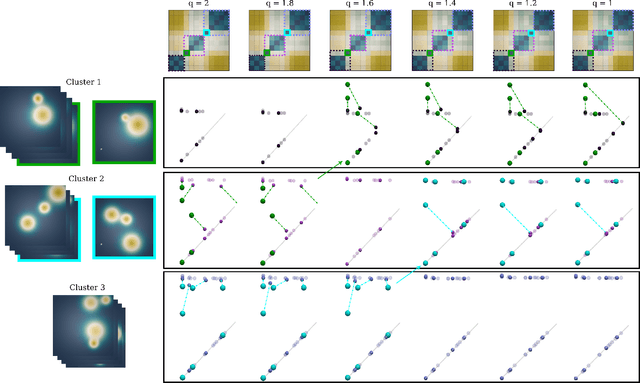
Abstract:This short paper presents a general approach for computing robust Wasserstein barycenters of persistence diagrams. The classical method consists in computing assignment arithmetic means after finding the optimal transport plans between the barycenter and the persistence diagrams. However, this procedure only works for the transportation cost related to the $q$-Wasserstein distance $W_q$ when $q=2$. We adapt an alternative fixed-point method to compute a barycenter diagram for generic transportation costs ($q > 1$), in particular those robust to outliers, $q \in (1,2)$. We show the utility of our work in two applications: \emph{(i)} the clustering of persistence diagrams on their metric space and \emph{(ii)} the dictionary encoding of persistence diagrams. In both scenarios, we demonstrate the added robustness to outliers provided by our generalized framework. Our Python implementation is available at this address: https://github.com/Keanu-Sisouk/RobustBarycenter .
Topology Aware Neural Interpolation of Scalar Fields
Aug 25, 2025Abstract:This paper presents a neural scheme for the topology-aware interpolation of time-varying scalar fields. Given a time-varying sequence of persistence diagrams, along with a sparse temporal sampling of the corresponding scalar fields, denoted as keyframes, our interpolation approach aims at "inverting" the non-keyframe diagrams to produce plausible estimations of the corresponding, missing data. For this, we rely on a neural architecture which learns the relation from a time value to the corresponding scalar field, based on the keyframe examples, and reliably extends this relation to the non-keyframe time steps. We show how augmenting this architecture with specific topological losses exploiting the input diagrams both improves the geometrical and topological reconstruction of the non-keyframe time steps. At query time, given an input time value for which an interpolation is desired, our approach instantaneously produces an output, via a single propagation of the time input through the network. Experiments interpolating 2D and 3D time-varying datasets show our approach superiority, both in terms of data and topological fitting, with regard to reference interpolation schemes.
A User's Guide to Sampling Strategies for Sliced Optimal Transport
Feb 05, 2025Abstract:This paper serves as a user's guide to sampling strategies for sliced optimal transport. We provide reminders and additional regularity results on the Sliced Wasserstein distance. We detail the construction methods, generation time complexity, theoretical guarantees, and conditions for each strategy. Additionally, we provide insights into their suitability for sliced optimal transport in theory. Extensive experiments on both simulated and real-world data offer a representative comparison of the strategies, culminating in practical recommendations for their best usage.
Wasserstein Dictionaries of Persistence Diagrams
Apr 28, 2023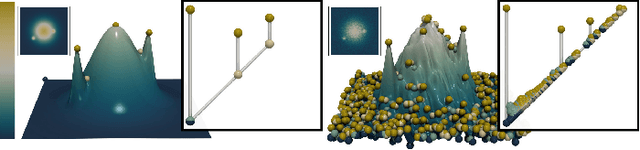
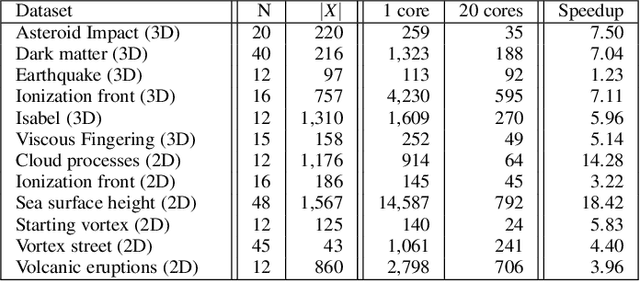
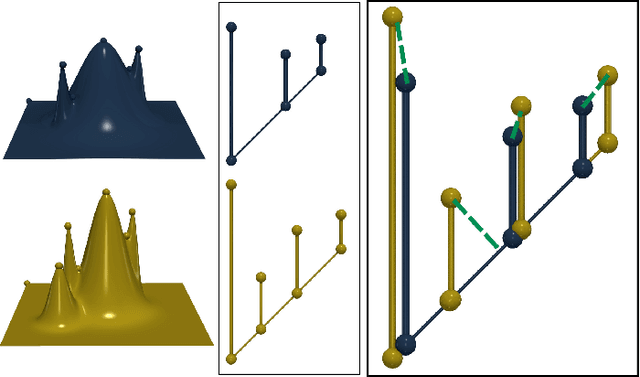
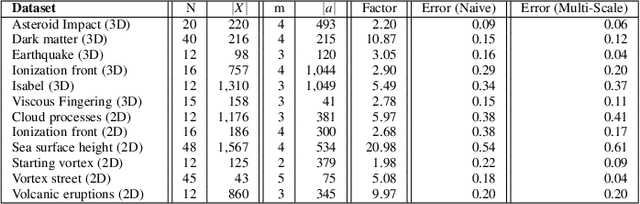
Abstract:This paper presents a computational framework for the concise encoding of an ensemble of persistence diagrams, in the form of weighted Wasserstein barycenters [99], [101] of a dictionary of atom diagrams. We introduce a multi-scale gradient descent approach for the efficient resolution of the corresponding minimization problem, which interleaves the optimization of the barycenter weights with the optimization of the atom diagrams. Our approach leverages the analytic expressions for the gradient of both sub-problems to ensure fast iterations and it additionally exploits shared-memory parallelism. Extensive experiments on public ensembles demonstrate the efficiency of our approach, with Wasserstein dictionary computations in the orders of minutes for the largest examples. We show the utility of our contributions in two applications. First, we apply Wassserstein dictionaries to data reduction and reliably compress persistence diagrams by concisely representing them with their weights in the dictionary. Second, we present a dimensionality reduction framework based on a Wasserstein dictionary defined with a small number of atoms (typically three) and encode the dictionary as a low dimensional simplex embedded in a visual space (typically in 2D). In both applications, quantitative experiments assess the relevance of our framework. Finally, we provide a C++ implementation that can be used to reproduce our results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge