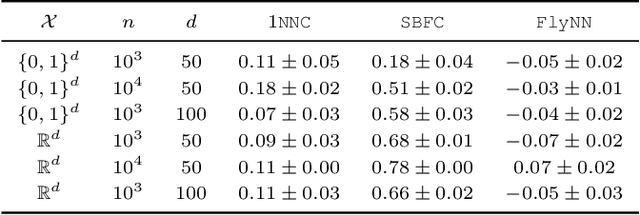
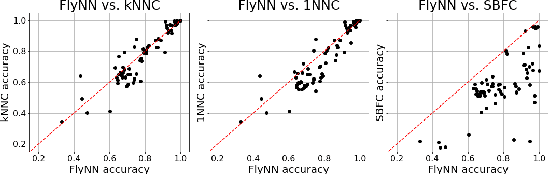
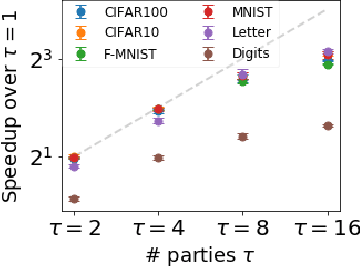
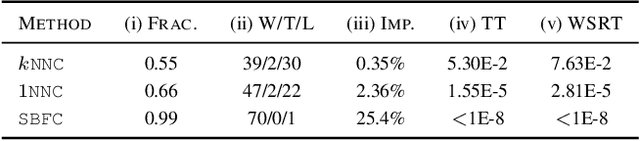
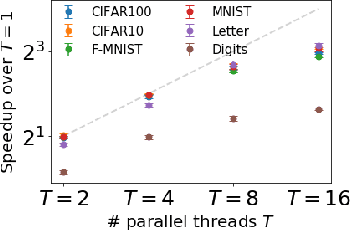
Federated Nearest Neighbor Classification with a Colony of Fruit-Flies: With Supplement

The mathematical formalization of a neurological mechanism in the olfactory circuit of a fruit-fly as a locality sensitive hash (Flyhash) and bloom filter (FBF) has been recently proposed and "reprogrammed" for various machine learning tasks such as similarity search, outlier detection and text embeddings. We propose a novel reprogramming of this hash and bloom filter to emulate the canonical nearest neighbor classifier (NNC) in the challenging Federated Learning (FL) setup where training and test data are spread across parties and no data can leave their respective parties. Specifically, we utilize Flyhash and FBF to create the FlyNN classifier, and theoretically establish conditions where FlyNN matches NNC. We show how FlyNN is trained exactly in a FL setup with low communication overhead to produce FlyNNFL, and how it can be differentially private. Empirically, we demonstrate that (i) FlyNN matches NNC accuracy across 70 OpenML datasets, (ii) FlyNNFL training is highly scalable with low communication overhead, providing up to $8\times$ speedup with $16$ parties.

Neural Neighborhood Encoding for Classification

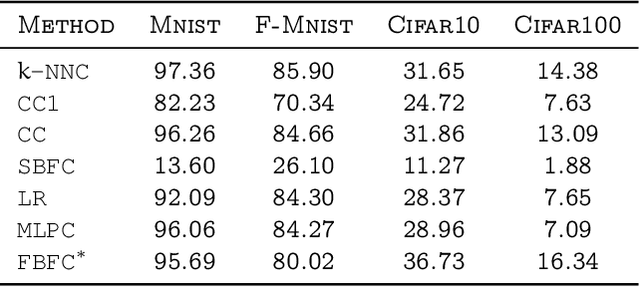
Inspired by the fruit-fly olfactory circuit, the Fly Bloom Filter [Dasgupta et al., 2018] is able to efficiently summarize the data with a single pass and has been used for novelty detection. We propose a new classifier (for binary and multi-class classification) that effectively encodes the different local neighborhoods for each class with a per-class Fly Bloom Filter. The inference on test data requires an efficient {\tt FlyHash} [Dasgupta, et al., 2017] operation followed by a high-dimensional, but {\em sparse}, dot product with the per-class Bloom Filters. The learning is trivially parallelizable. On the theoretical side, we establish conditions under which the prediction of our proposed classifier on any test example agrees with the prediction of the nearest neighbor classifier with high probability. We extensively evaluate our proposed scheme with over $50$ data sets of varied data dimensionality to demonstrate that the predictive performance of our proposed neuroscience inspired classifier is competitive the the nearest-neighbor classifiers and other single-pass classifiers.

Near-Optimal Algorithms for Differentially-Private Principal Components

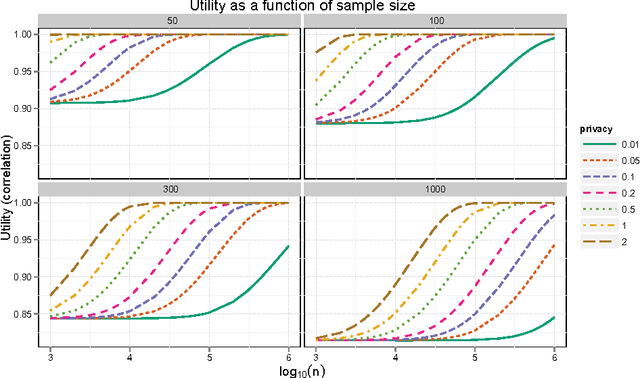
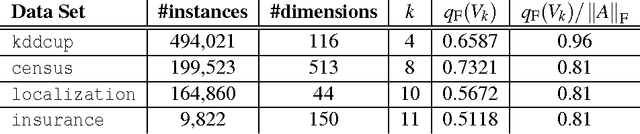
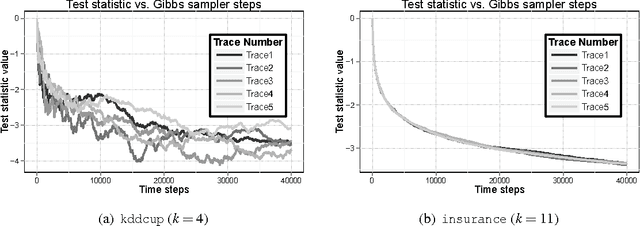
Principal components analysis (PCA) is a standard tool for identifying good low-dimensional approximations to data in high dimension. Many data sets of interest contain private or sensitive information about individuals. Algorithms which operate on such data should be sensitive to the privacy risks in publishing their outputs. Differential privacy is a framework for developing tradeoffs between privacy and the utility of these outputs. In this paper we investigate the theory and empirical performance of differentially private approximations to PCA and propose a new method which explicitly optimizes the utility of the output. We show that the sample complexity of the proposed method differs from the existing procedure in the scaling with the data dimension, and that our method is nearly optimal in terms of this scaling. We furthermore illustrate our results, showing that on real data there is a large performance gap between the existing method and our method.

Learning Gaussian Mixtures with Arbitrary Separation

In this paper we present a method for learning the parameters of a mixture of $k$ identical spherical Gaussians in $n$-dimensional space with an arbitrarily small separation between the components. Our algorithm is polynomial in all parameters other than $k$. The algorithm is based on an appropriate grid search over the space of parameters. The theoretical analysis of the algorithm hinges on a reduction of the problem to 1 dimension and showing that two 1-dimensional mixtures whose densities are close in the $L^2$ norm must have similar means and mixing coefficients. To produce such a lower bound for the $L^2$ norm in terms of the distances between the corresponding means, we analyze the behavior of the Fourier transform of a mixture of Gaussians in 1 dimension around the origin, which turns out to be closely related to the properties of the Vandermonde matrix obtained from the component means. Analysis of this matrix together with basic function approximation results allows us to provide a lower bound for the norm of the mixture in the Fourier domain. In recent years much research has been aimed at understanding the computational aspects of learning parameters of Gaussians mixture distributions in high dimension. To the best of our knowledge all existing work on learning parameters of Gaussian mixtures assumes minimum separation between components of the mixture which is an increasing function of either the dimension of the space $n$ or the number of components $k$. In our paper we prove the first result showing that parameters of a $n$-dimensional Gaussian mixture model with arbitrarily small component separation can be learned in time polynomial in $n$.

Polynomial Learning of Distribution Families

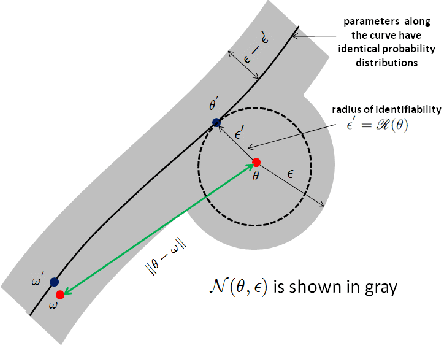
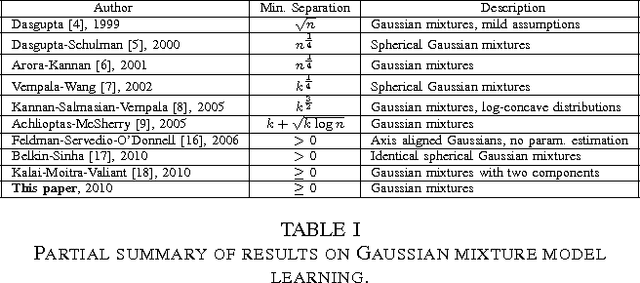
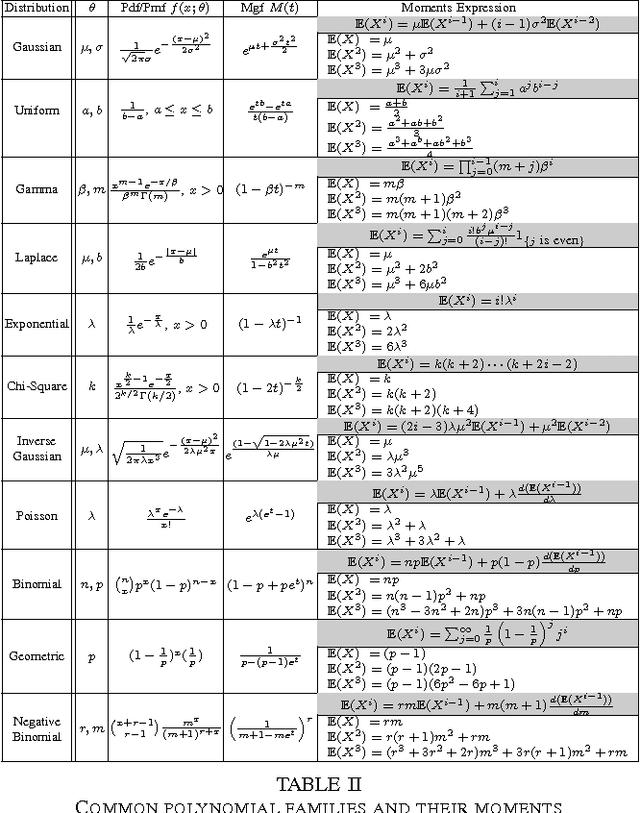
The question of polynomial learnability of probability distributions, particularly Gaussian mixture distributions, has recently received significant attention in theoretical computer science and machine learning. However, despite major progress, the general question of polynomial learnability of Gaussian mixture distributions still remained open. The current work resolves the question of polynomial learnability for Gaussian mixtures in high dimension with an arbitrary fixed number of components. The result on learning Gaussian mixtures relies on an analysis of distributions belonging to what we call "polynomial families" in low dimension. These families are characterized by their moments being polynomial in parameters and include almost all common probability distributions as well as their mixtures and products. Using tools from real algebraic geometry, we show that parameters of any distribution belonging to such a family can be learned in polynomial time and using a polynomial number of sample points. The result on learning polynomial families is quite general and is of independent interest. To estimate parameters of a Gaussian mixture distribution in high dimensions, we provide a deterministic algorithm for dimensionality reduction. This allows us to reduce learning a high-dimensional mixture to a polynomial number of parameter estimations in low dimension. Combining this reduction with the results on polynomial families yields our result on learning arbitrary Gaussian mixtures in high dimensions.