Glucagon and insulin production in pancreatic cells modeled using Petri nets and Boolean networks

Diabetes is a civilization chronic disease characterized by a constant elevated concentration of glucose in the blood. Many processes are involved in the glucose regulation, and their interactions are very complex. To better understand those processes we set ourselves a goal to create a Petri net model of the glucose regulation in the whole body. So far we have managed to create a model of glycolysis and synthesis of glucose in the liver, and the general overview models of the glucose regulation in a healthy and diabetic person. In this paper we introduce Petri nets models of insulin secretion in beta cell of the pancreas, and glucagon in the pancreas alpha cells. Those two hormones have mutually opposite effects: insulin preventing hyperglycemia, and glucagon preventing hypoglycemia. Understanding the mechanisms of insulin and glucagon secretion constitutes the basis for understanding diabetes. We also present a model in which both processes occur together, depending on the blood glucose level. The dynamics of each model is analysed. Additionally, we transform the overall insulin and glucagon secretion system to a Boolean network, following standard transformation rules.

Petri nets in modelling glucose regulating processes in the liver

Diabetes is a chronic condition, considered one of the civilization diseases, that is characterized by sustained high blood sugar levels. There is no doubt that more and more people is going to suffer from diabetes, hence it is crucial to understand better its biological foundations. The essential processes related to the control of glucose levels in the blood are: glycolysis (process of breaking down of glucose) and glucose synthesis, both taking place in the liver. The glycolysis occurs during feeding and it is stimulated by insulin. On the other hand, the glucose synthesis arises during fasting and it is stimulated by glucagon. In the paper we present a Petri net model of glycolysis and glucose synthesis in the liver. The model is created based on medical literature. Standard Petri nets techniques are used to analyse the properties of the model: traps, reachability graphs, tokens dynamics, deadlocks analysis. The results are described in the paper. Our analysis shows that the model captures the interactions between different enzymes and substances, which is consistent with the biological processes occurring during fasting and feeding. The model constitutes the first element of our long-time goal to create the whole body model of the glucose regulation in a healthy human and a person with diabetes.

Formal Translation from Reversing Petri Nets to Coloured Petri Nets

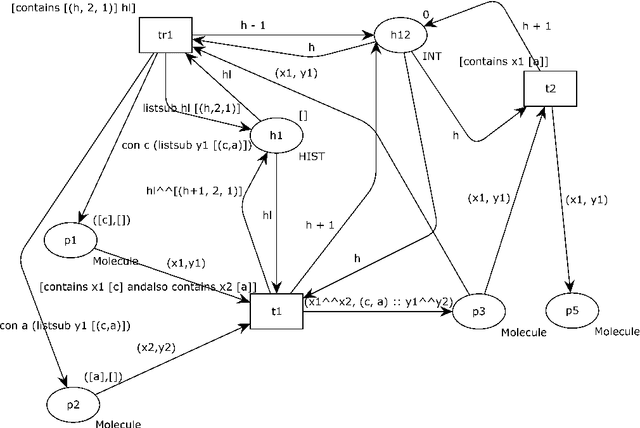
Reversible computation is an emerging computing paradigm that allows any sequence of operations to be executed in reverse order at any point during computation. Its appeal lies in its potential for lowpower computation and its relevance to a wide array of applications such as chemical reactions, quantum computation, robotics, and distributed systems. Reversing Petri nets are a recently-proposed extension of Petri nets that implements the three main forms of reversibility, namely, backtracking, causal reversing, and out-of-causal-order reversing. Their distinguishing feature is the use of named tokens that can be combined together to form bonds. Named tokens along with a history function, constitute the means of remembering past behaviour, thus, enabling reversal. In recent work, we have proposed a structural translation from a subclass of RPNs to the model of Coloured Petri Nets (CPNs), an extension of traditional Petri nets where tokens carry data values. In this paper, we extend the translation to handle RPNs with token multiplicity under the individual-token interpretation, a model which allows multiple tokens of the same type to exist in a system. To support the three types of reversibility, tokens are associated with their causal history and, while tokens of the same type are equally eligible to fire a transition when going forward, when going backwards they are able to reverse only the transitions they have previously fired. The new translation, in addition to lifting the restriction on token uniqueness, presents a refined approach for transforming RPNs to CPNs through a unifying approach that allows instantiating each of the three types of reversibility. The paper also reports on a tool that implements this translation, paving the way for automated translations and analysis of reversible systems using CPN Tools.

Acyclic and Cyclic Reversing Computations in Petri Nets

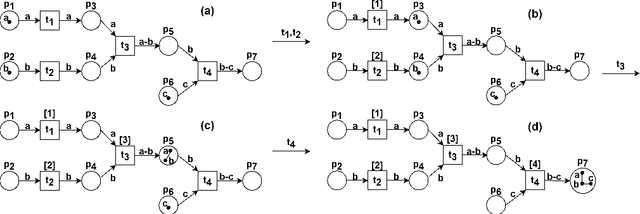
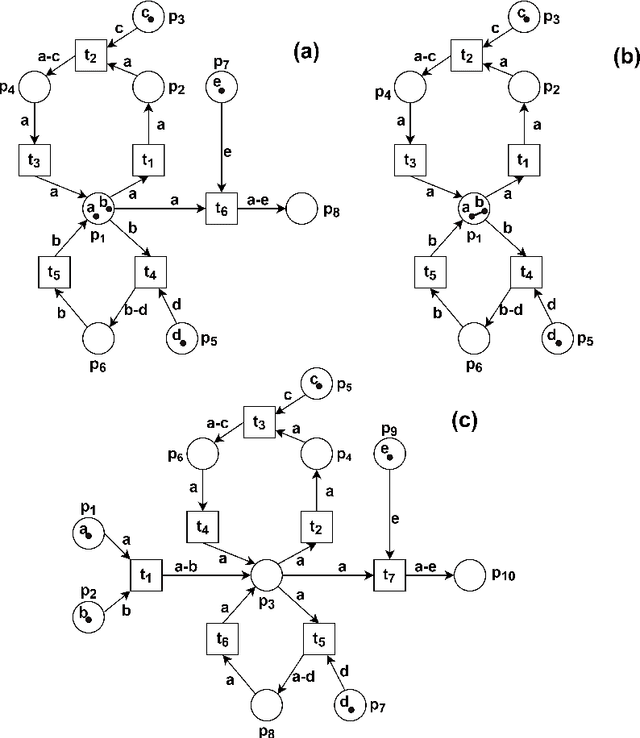
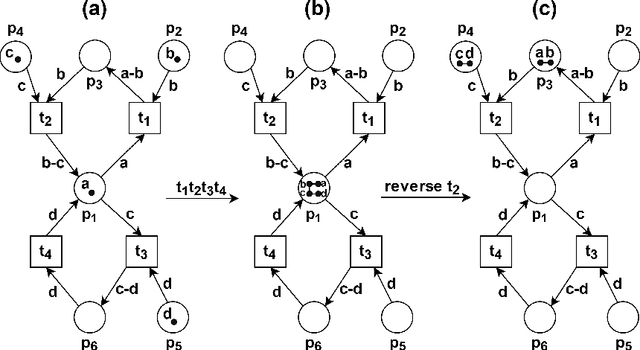
Reversible computations constitute an unconventional form of computing where any sequence of performed operations can be undone by executing in reverse order at any point during a computation. It has been attracting increasing attention as it provides opportunities for low-power computation, being at the same time essential or eligible in various applications. In recent work, we have proposed a structural way of translating Reversing Petri Nets (RPNs) - a type of Petri nets that embeds reversible computation, to bounded Coloured Petri Nets (CPNs) - an extension of traditional Petri Nets, where tokens carry data values. Three reversing semantics are possible in RPNs: backtracking (reversing of the lately executed action), causal reversing (action can be reversed only when all its effects have been undone) and out of causal reversing (any previously performed action can be reversed). In this paper, we extend the RPN to CPN translation with formal proofs of correctness. Moreover, the possibility of introduction of cycles to RPNs is discussed. We analyze which type of cycles could be allowed in RPNs to ensure consistency with the current semantics. It emerged that the most interesting case related to cycles in RPNs occurs in causal semantics, where various interpretations of dependency result in different net's behaviour during reversing. Three definitions of dependence are presented and discussed.