More About Covariance Descriptors for Image Set Coding: Log-Euclidean Framework based Kernel Matrix Representation

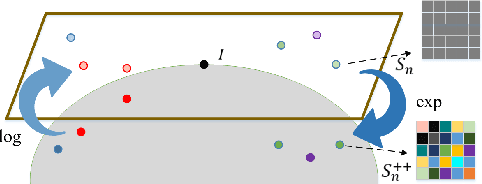
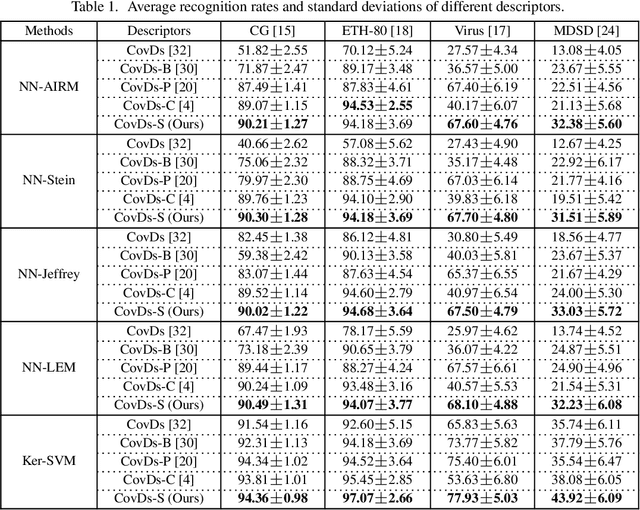
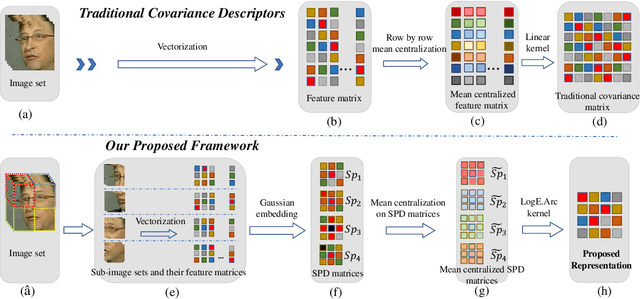
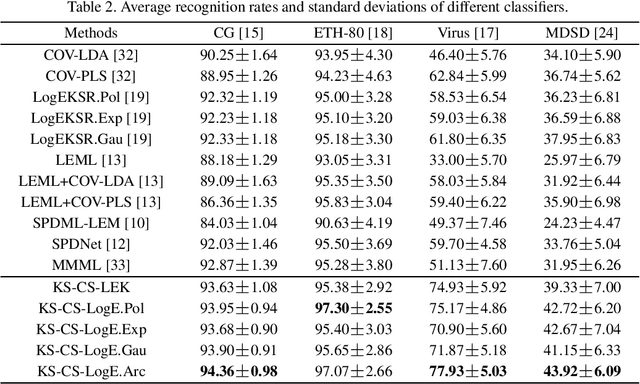
We consider a family of structural descriptors for visual data, namely covariance descriptors (CovDs) that lie on a non-linear symmetric positive definite (SPD) manifold, a special type of Riemannian manifolds. We propose an improved version of CovDs for image set coding by extending the traditional CovDs from Euclidean space to the SPD manifold. Specifically, the manifold of SPD matrices is a complete inner product space with the operations of logarithmic multiplication and scalar logarithmic multiplication defined in the Log-Euclidean framework. In this framework, we characterise covariance structure in terms of the arc-cosine kernel which satisfies Mercer's condition and propose the operation of mean centralization on SPD matrices. Furthermore, we combine arc-cosine kernels of different orders using mixing parameters learnt by kernel alignment in a supervised manner. Our proposed framework provides a lower-dimensional and more discriminative data representation for the task of image set classification. The experimental results demonstrate its superior performance, measured in terms of recognition accuracy, as compared with the state-of-the-art methods.

Grassmannian Discriminant Maps (GDM) for Manifold Dimensionality Reduction with Application to Image Set Classification

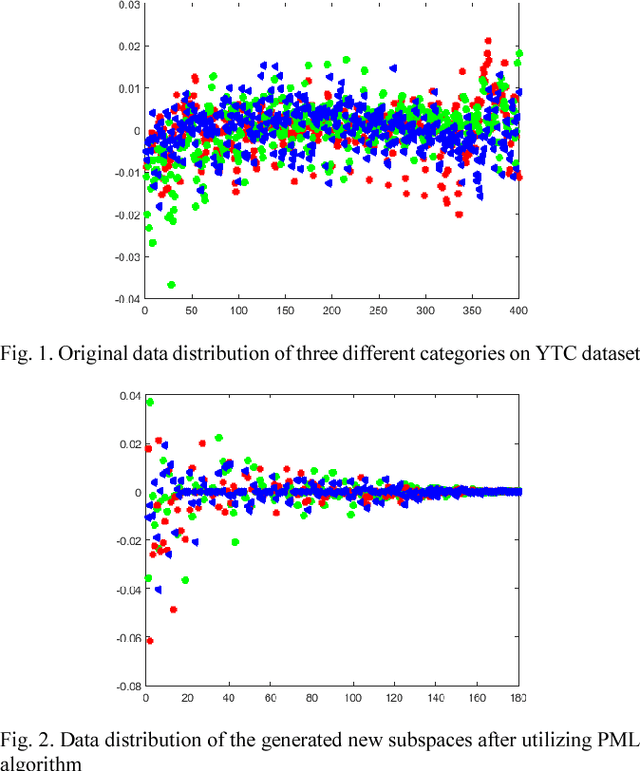
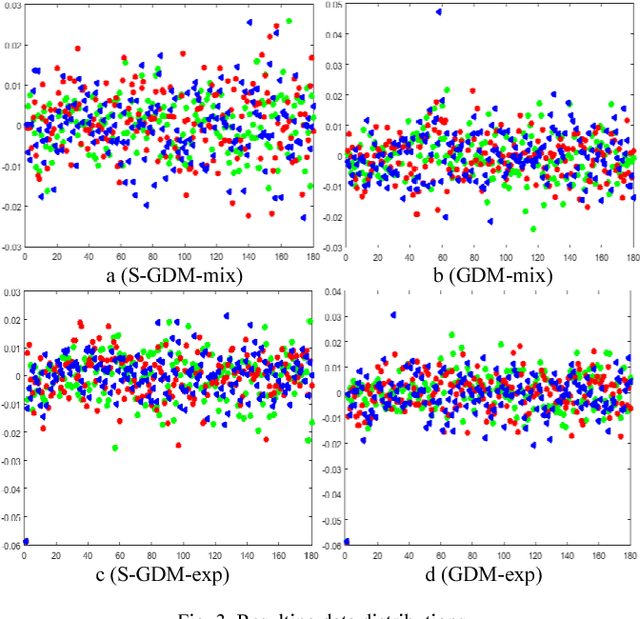
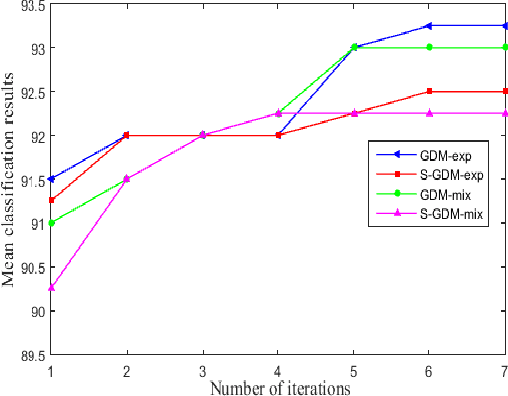
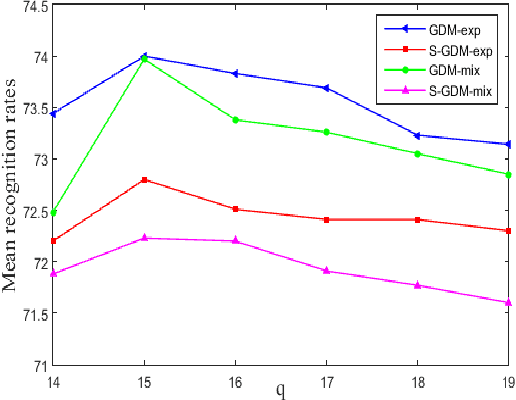
In image set classification, a considerable progress has been made by representing original image sets on Grassmann manifolds. In order to extend the advantages of the Euclidean based dimensionality reduction methods to the Grassmann Manifold, several methods have been suggested recently which jointly perform dimensionality reduction and metric learning on Grassmann manifold to improve performance. Nevertheless, when applied to complex datasets, the learned features do not exhibit enough discriminatory power. To overcome this problem, we propose a new method named Grassmannian Discriminant Maps (GDM) for manifold dimensionality reduction problems. The core of the method is a new discriminant function for metric learning and dimensionality reduction. For comparison and better understanding, we also study a simple variations to GDM. The key difference between them is the discriminant function. We experiment on data sets corresponding to three tasks: face recognition, object categorization, and hand gesture recognition to evaluate the proposed method and its simple extensions. Compared with the state of the art, the results achieved show the effectiveness of the proposed algorithm.

Component SPD Matrices: A lower-dimensional discriminative data descriptor for image set classification

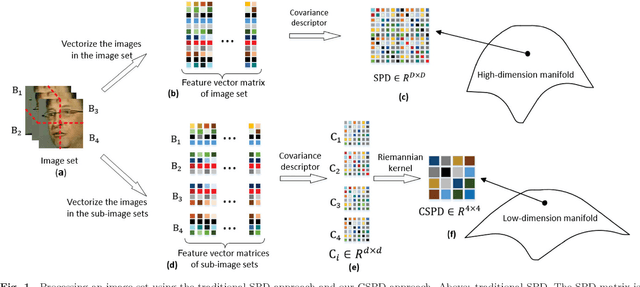
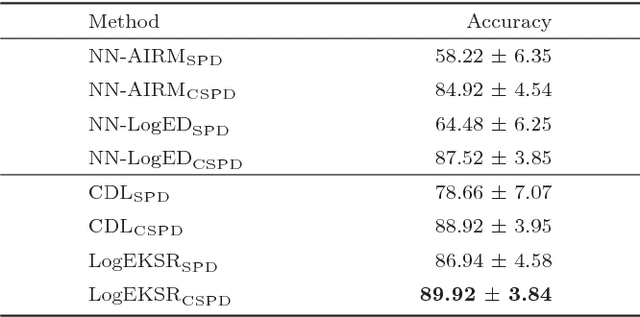
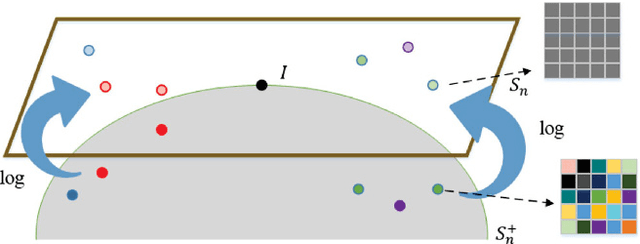
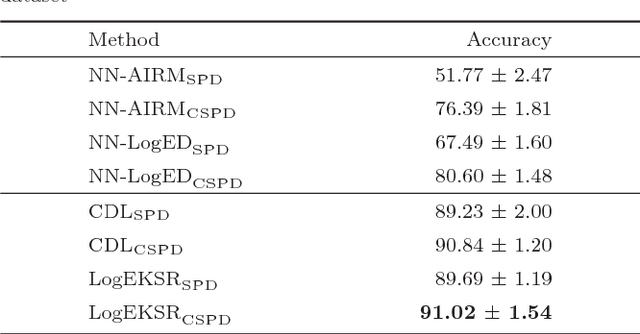
In the domain of pattern recognition, using the SPD (Symmetric Positive Definite) matrices to represent data and taking the metrics of resulting Riemannian manifold into account have been widely used for the task of image set classification. In this paper, we propose a new data representation framework for image sets named CSPD (Component Symmetric Positive Definite). Firstly, we obtain sub-image sets by dividing the image set into square blocks with the same size, and use traditional SPD model to describe them. Then, we use the results of the Riemannian kernel on SPD matrices as similarities of corresponding sub-image sets. Finally, the CSPD matrix appears in the form of the kernel matrix for all the sub-image sets, and CSPDi,j denotes the similarity between i-th sub-image set and j-th sub-image set. Here, the Riemannian kernel is shown to satisfy the Mercer's theorem, so our proposed CSPD matrix is symmetric and positive definite and also lies on a Riemannian manifold. On three benchmark datasets, experimental results show that CSPD is a lower-dimensional and more discriminative data descriptor for the task of image set classification.

Riemannian kernel based Nyström method for approximate infinite-dimensional covariance descriptors with application to image set classification

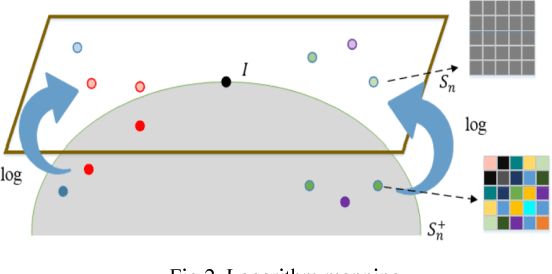
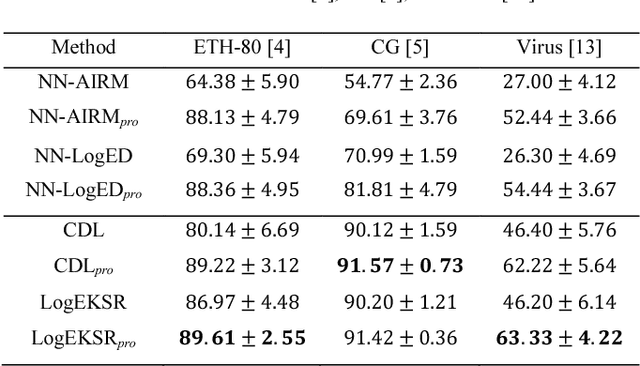
In the domain of pattern recognition, using the CovDs (Covariance Descriptors) to represent data and taking the metrics of the resulting Riemannian manifold into account have been widely adopted for the task of image set classification. Recently, it has been proven that infinite-dimensional CovDs are more discriminative than their low-dimensional counterparts. However, the form of infinite-dimensional CovDs is implicit and the computational load is high. We propose a novel framework for representing image sets by approximating infinite-dimensional CovDs in the paradigm of the Nystr\"om method based on a Riemannian kernel. We start by modeling the images via CovDs, which lie on the Riemannian manifold spanned by SPD (Symmetric Positive Definite) matrices. We then extend the Nystr\"om method to the SPD manifold and obtain the approximations of CovDs in RKHS (Reproducing Kernel Hilbert Space). Finally, we approximate infinite-dimensional CovDs via these approximations. Empirically, we apply our framework to the task of image set classification. The experimental results obtained on three benchmark datasets show that our proposed approximate infinite-dimensional CovDs outperform the original CovDs.

Multiple Manifolds Metric Learning with Application to Image Set Classification

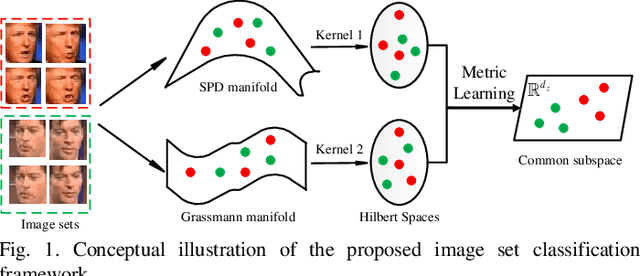
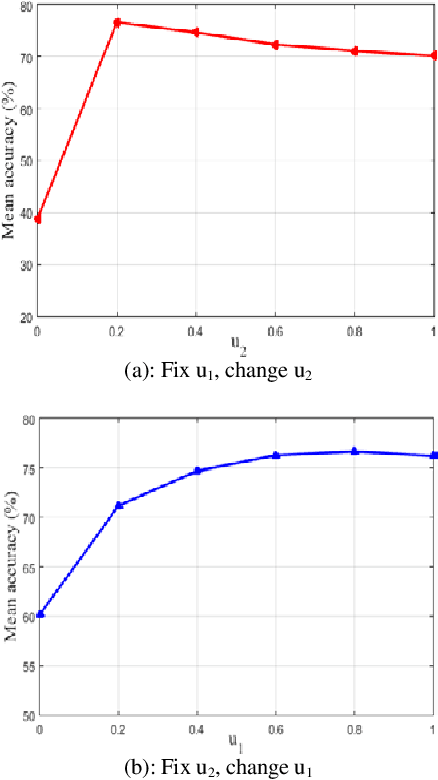
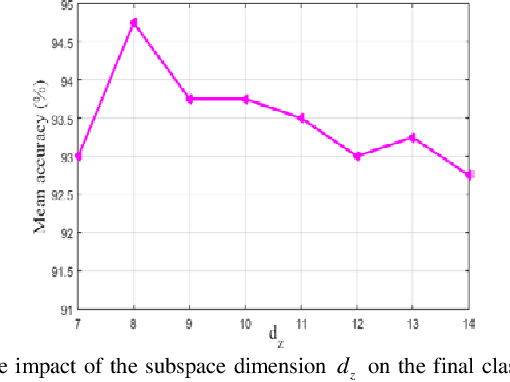
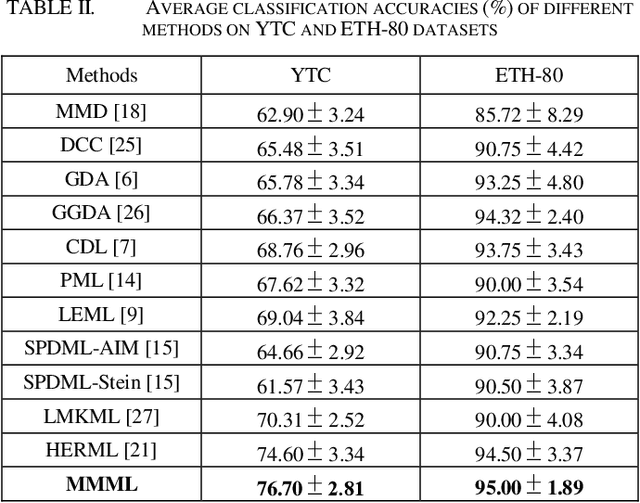
In image set classification, a considerable advance has been made by modeling the original image sets by second order statistics or linear subspace, which typically lie on the Riemannian manifold. Specifically, they are Symmetric Positive Definite (SPD) manifold and Grassmann manifold respectively, and some algorithms have been developed on them for classification tasks. Motivated by the inability of existing methods to extract discriminatory features for data on Riemannian manifolds, we propose a novel algorithm which combines multiple manifolds as the features of the original image sets. In order to fuse these manifolds, the well-studied Riemannian kernels have been utilized to map the original Riemannian spaces into high dimensional Hilbert spaces. A metric Learning method has been devised to embed these kernel spaces into a lower dimensional common subspace for classification. The state-of-the-art results achieved on three datasets corresponding to two different classification tasks, namely face recognition and object categorization, demonstrate the effectiveness of the proposed method.