On non-iterative training of a neural classifier

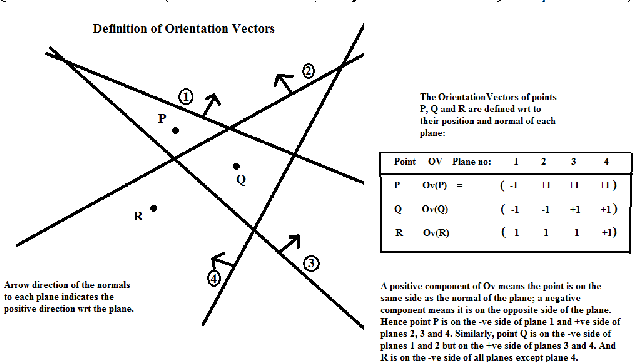
Recently an algorithm, was discovered, which separates points in n-dimension by planes in such a manner that no two points are left un-separated by at least one plane{[}1-3{]}. By using this new algorithm we show that there are two ways of classification by a neural network, for a large dimension feature space, both of which are non-iterative and deterministic. To demonstrate the power of both these methods we apply them exhaustively to the classical pattern recognition problem: The Fisher-Anderson's, IRIS flower data set and present the results. It is expected these methods will now be widely used for the training of neural networks for Deep Learning not only because of their non-iterative and deterministic nature but also because of their efficiency and speed and will supersede other classification methods which are iterative in nature and rely on error minimization.

Some Theorems for Feed Forward Neural Networks

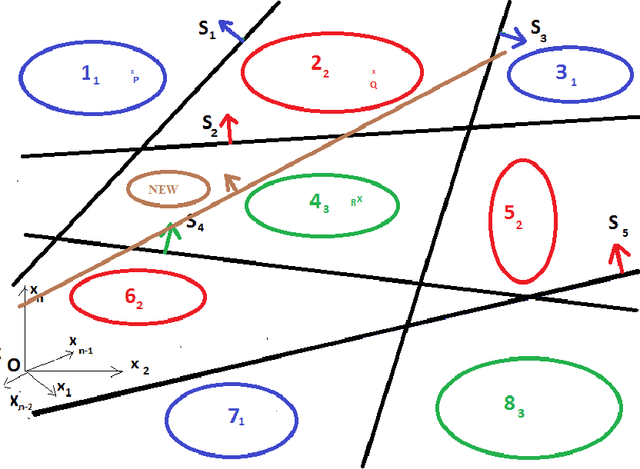
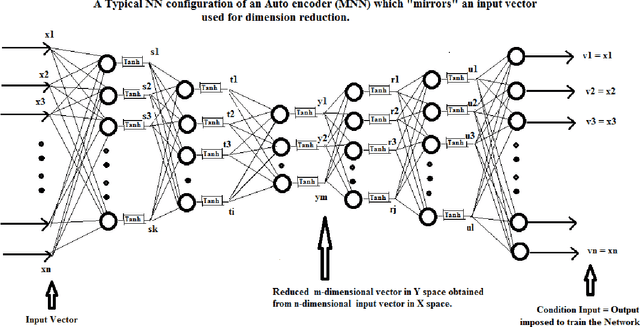
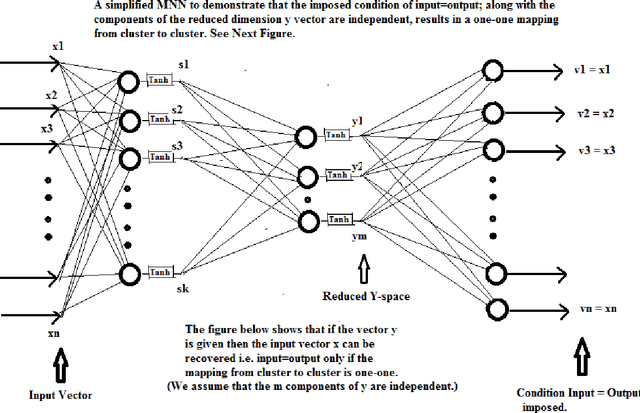
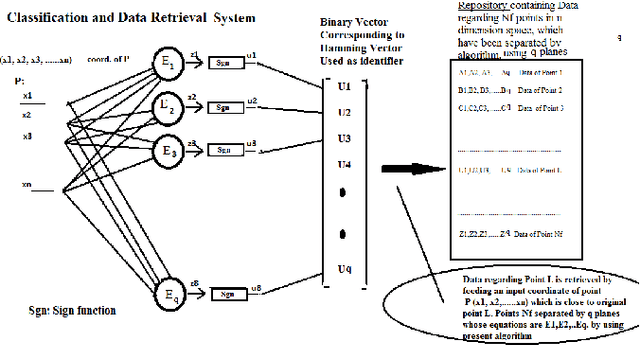
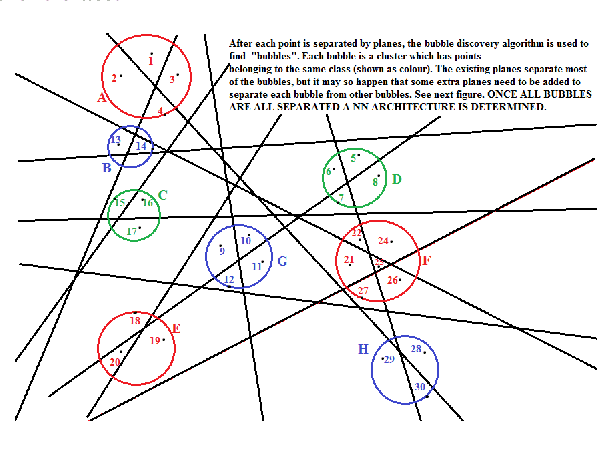
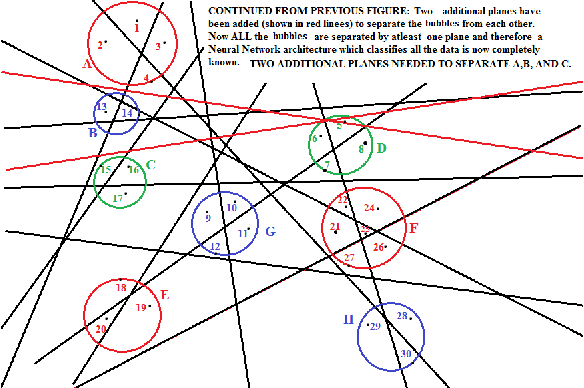
In this paper we introduce a new method which employs the concept of "Orientation Vectors" to train a feed forward neural network and suitable for problems where large dimensions are involved and the clusters are characteristically sparse. The new method is not NP hard as the problem size increases. We `derive' the method by starting from Kolmogrov's method and then relax some of the stringent conditions. We show for most classification problems three layers are sufficient and the network size depends on the number of clusters. We prove as the number of clusters increase from N to N+dN the number of processing elements in the first layer only increases by d(logN), and are proportional to the number of classes, and the method is not NP hard. Many examples are solved to demonstrate that the method of Orientation Vectors requires much less computational effort than Radial Basis Function methods and other techniques wherein distance computations are required, in fact the present method increases logarithmically with problem size compared to the Radial Basis Function method and the other methods which depend on distance computations e.g statistical methods where probabilistic distances are calculated. A practical method of applying the concept of Occum's razor to choose between two architectures which solve the same classification problem has been described. The ramifications of the above findings on the field of Deep Learning have also been briefly investigated and we have found that it directly leads to the existence of certain types of NN architectures which can be used as a "mapping engine", which has the property of "invertibility", thus improving the prospect of their deployment for solving problems involving Deep Learning and hierarchical classification. The latter possibility has a lot of future scope in the areas of machine learning and cloud computing.

A Mirroring Theorem and its Application to a New Method of Unsupervised Hierarchical Pattern Classification

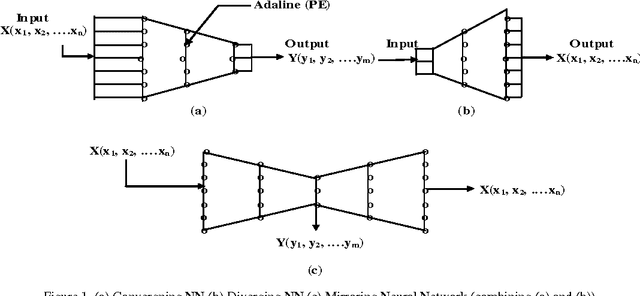
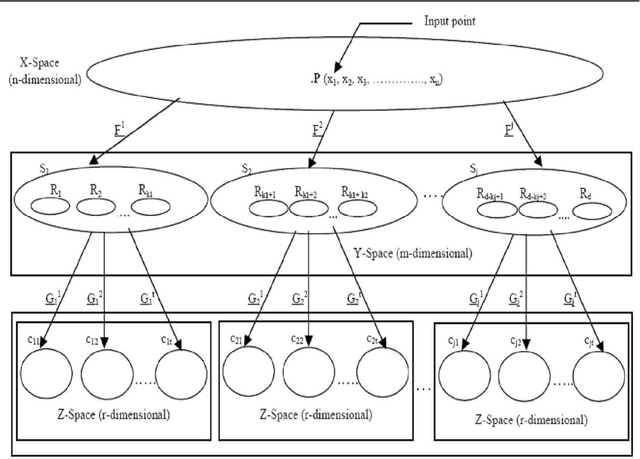
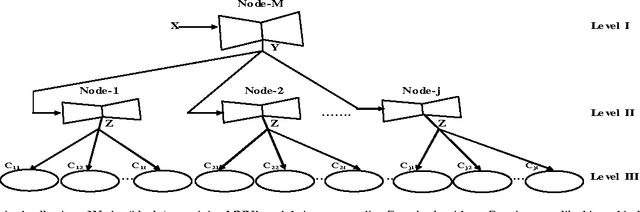
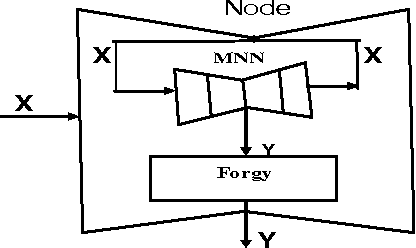
In this paper, we prove a crucial theorem called Mirroring Theorem which affirms that given a collection of samples with enough information in it such that it can be classified into classes and subclasses then (i) There exists a mapping which classifies and subclassifies these samples (ii) There exists a hierarchical classifier which can be constructed by using Mirroring Neural Networks (MNNs) in combination with a clustering algorithm that can approximate this mapping. Thus, the proof of the Mirroring theorem provides a theoretical basis for the existence and a practical feasibility of constructing hierarchical classifiers, given the maps. Our proposed Mirroring Theorem can also be considered as an extension to Kolmogrovs theorem in providing a realistic solution for unsupervised classification. The techniques we develop, are general in nature and have led to the construction of learning machines which are (i) tree like in structure, (ii) modular (iii) with each module running on a common algorithm (tandem algorithm) and (iv) selfsupervised. We have actually built the architecture, developed the tandem algorithm of such a hierarchical classifier and demonstrated it on an example problem.

Pattern Recognition and Memory Mapping using Mirroring Neural Networks

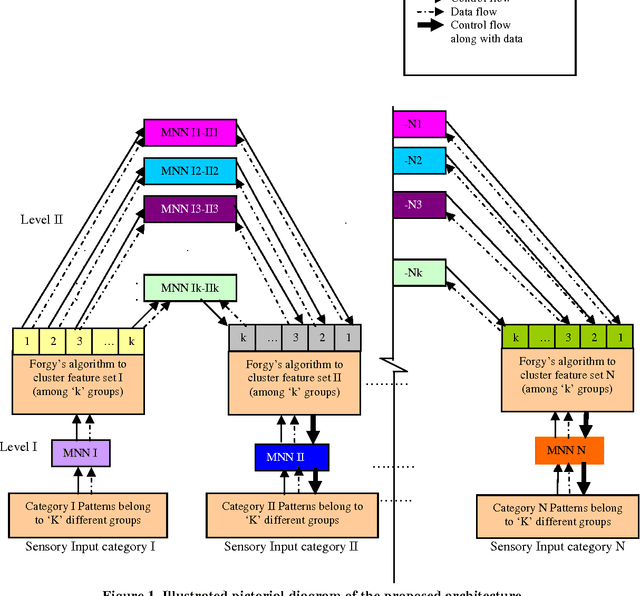
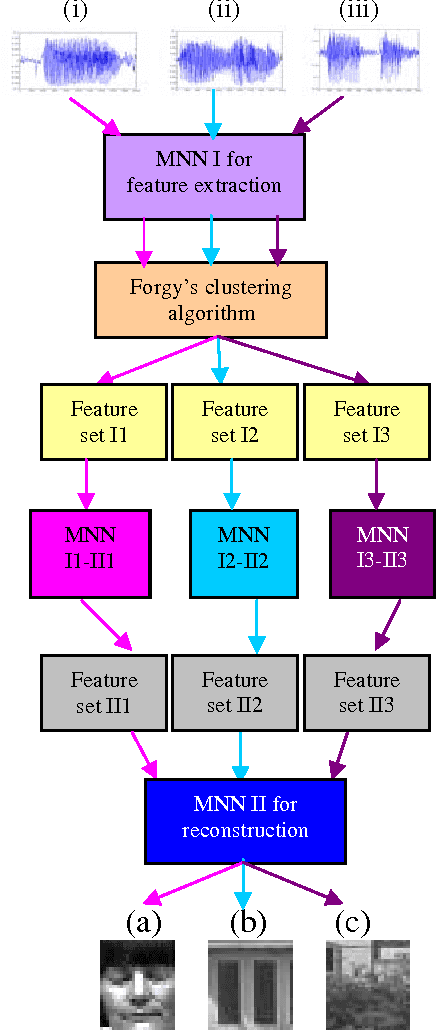
In this paper, we present a new kind of learning implementation to recognize the patterns using the concept of Mirroring Neural Network (MNN) which can extract information from distinct sensory input patterns and perform pattern recognition tasks. It is also capable of being used as an advanced associative memory wherein image data is associated with voice inputs in an unsupervised manner. Since the architecture is hierarchical and modular it has the potential of being used to devise learning engines of ever increasing complexity.

Dimensionality Reduction and Reconstruction using Mirroring Neural Networks and Object Recognition based on Reduced Dimension Characteristic Vector

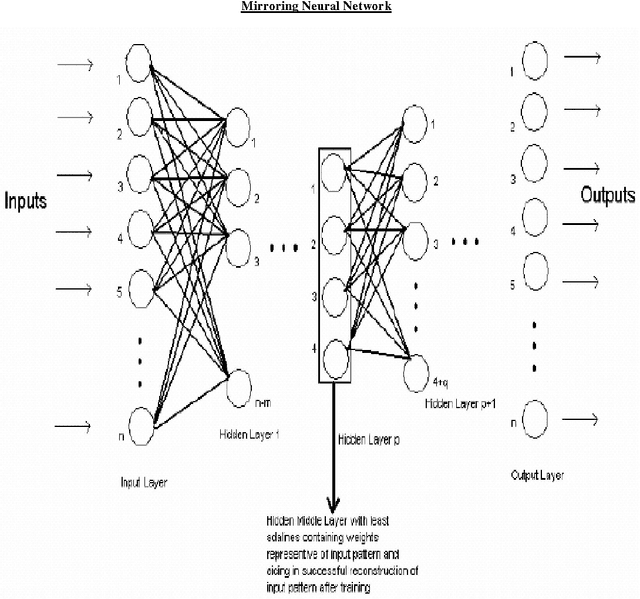
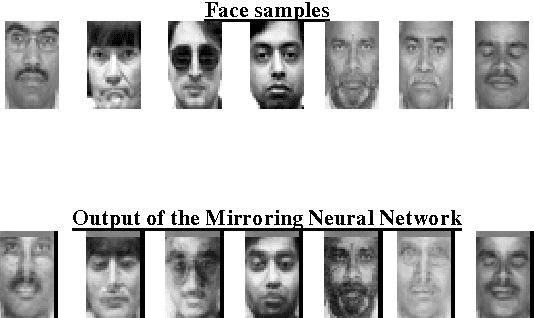
In this paper, we present a Mirroring Neural Network architecture to perform non-linear dimensionality reduction and Object Recognition using a reduced lowdimensional characteristic vector. In addition to dimensionality reduction, the network also reconstructs (mirrors) the original high-dimensional input vector from the reduced low-dimensional data. The Mirroring Neural Network architecture has more number of processing elements (adalines) in the outer layers and the least number of elements in the central layer to form a converging-diverging shape in its configuration. Since this network is able to reconstruct the original image from the output of the innermost layer (which contains all the information about the input pattern), these outputs can be used as object signature to classify patterns. The network is trained to minimize the discrepancy between actual output and the input by back propagating the mean squared error from the output layer to the input layer. After successfully training the network, it can reduce the dimension of input vectors and mirror the patterns fed to it. The Mirroring Neural Network architecture gave very good results on various test patterns.

Automatic Pattern Classification by Unsupervised Learning Using Dimensionality Reduction of Data with Mirroring Neural Networks

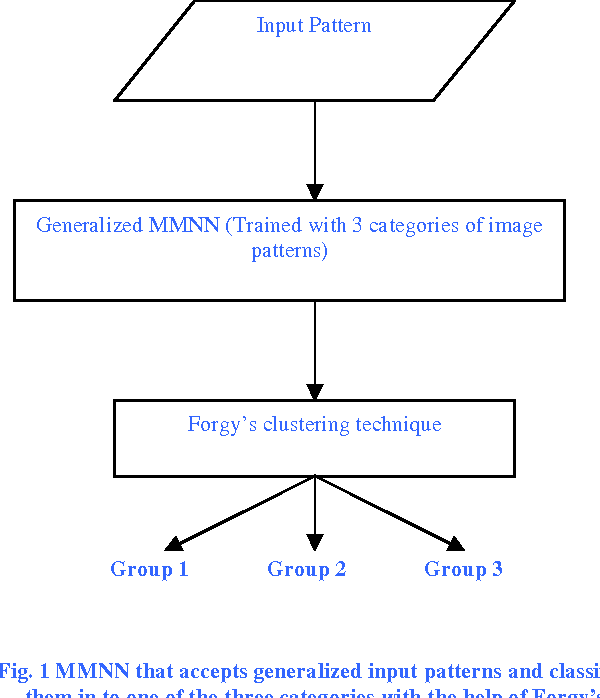
This paper proposes an unsupervised learning technique by using Multi-layer Mirroring Neural Network and Forgy's clustering algorithm. Multi-layer Mirroring Neural Network is a neural network that can be trained with generalized data inputs (different categories of image patterns) to perform non-linear dimensionality reduction and the resultant low-dimensional code is used for unsupervised pattern classification using Forgy's algorithm. By adapting the non-linear activation function (modified sigmoidal function) and initializing the weights and bias terms to small random values, mirroring of the input pattern is initiated. In training, the weights and bias terms are changed in such a way that the input presented is reproduced at the output by back propagating the error. The mirroring neural network is capable of reducing the input vector to a great degree (approximately 1/30th the original size) and also able to reconstruct the input pattern at the output layer from this reduced code units. The feature set (output of central hidden layer) extracted from this network is fed to Forgy's algorithm, which classify input data patterns into distinguishable classes. In the implementation of Forgy's algorithm, initial seed points are selected in such a way that they are distant enough to be perfectly grouped into different categories. Thus a new method of unsupervised learning is formulated and demonstrated in this paper. This method gave impressive results when applied to classification of different image patterns.