On learning functions over biological sequence space: relating Gaussian process priors, regularization, and gauge fixing

Mappings from biological sequences (DNA, RNA, protein) to quantitative measures of sequence functionality play an important role in contemporary biology. We are interested in the related tasks of (i) inferring predictive sequence-to-function maps and (ii) decomposing sequence-function maps to elucidate the contributions of individual subsequences. Because each sequence-function map can be written as a weighted sum over subsequences in multiple ways, meaningfully interpreting these weights requires "gauge-fixing," i.e., defining a unique representation for each map. Recent work has established that most existing gauge-fixed representations arise as the unique solutions to $L_2$-regularized regression in an overparameterized "weight space" where the choice of regularizer defines the gauge. Here, we establish the relationship between regularized regression in overparameterized weight space and Gaussian process approaches that operate in "function space," i.e. the space of all real-valued functions on a finite set of sequences. We disentangle how weight space regularizers both impose an implicit prior on the learned function and restrict the optimal weights to a particular gauge. We also show how to construct regularizers that correspond to arbitrary explicit Gaussian process priors combined with a wide variety of gauges. Next, we derive the distribution of gauge-fixed weights implied by the Gaussian process posterior and demonstrate that even for long sequences this distribution can be efficiently computed for product-kernel priors using a kernel trick. Finally, we characterize the implicit function space priors associated with the most common weight space regularizers. Overall, our framework unifies and extends our ability to infer and interpret sequence-function relationships.

Biophysical models of cis-regulation as interpretable neural networks

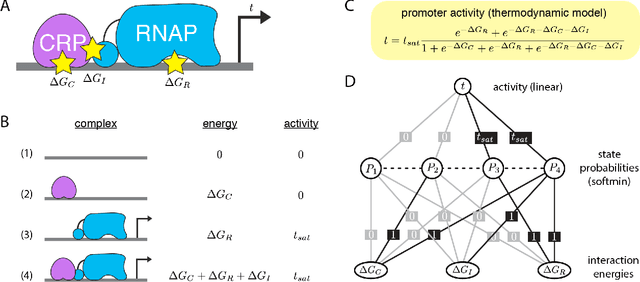
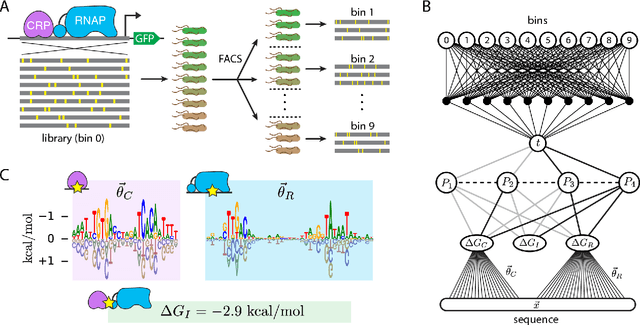
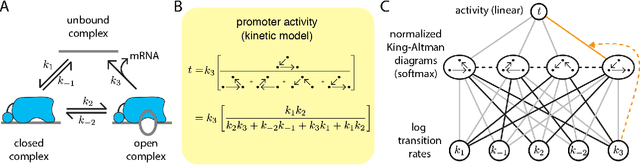
The adoption of deep learning techniques in genomics has been hindered by the difficulty of mechanistically interpreting the models that these techniques produce. In recent years, a variety of post-hoc attribution methods have been proposed for addressing this neural network interpretability problem in the context of gene regulation. Here we describe a complementary way of approaching this problem. Our strategy is based on the observation that two large classes of biophysical models of cis-regulatory mechanisms can be expressed as deep neural networks in which nodes and weights have explicit physiochemical interpretations. We also demonstrate how such biophysical networks can be rapidly inferred, using modern deep learning frameworks, from the data produced by certain types of massively parallel reporter assays (MPRAs). These results suggest a scalable strategy for using MPRAs to systematically characterize the biophysical basis of gene regulation in a wide range of biological contexts. They also highlight gene regulation as a promising venue for the development of scientifically interpretable approaches to deep learning.

Learning quantitative sequence-function relationships from massively parallel experiments

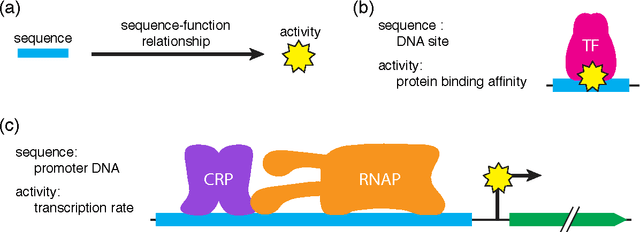
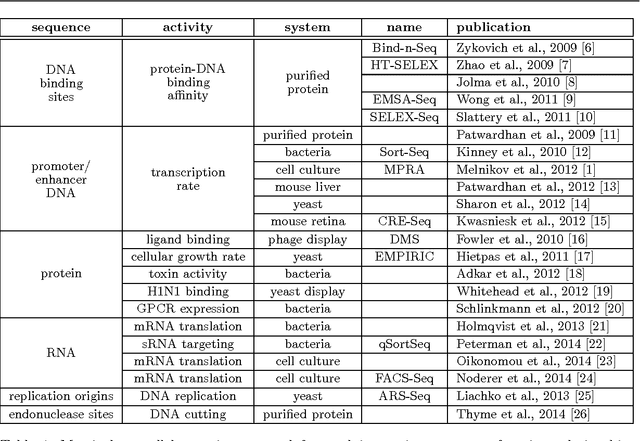
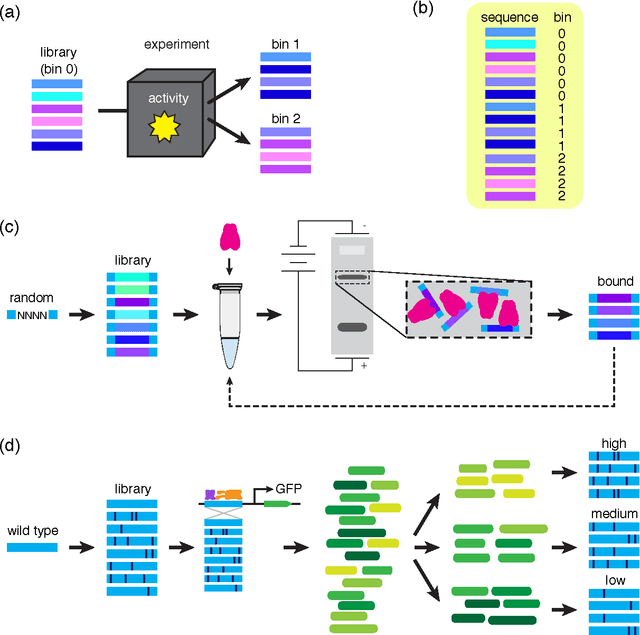
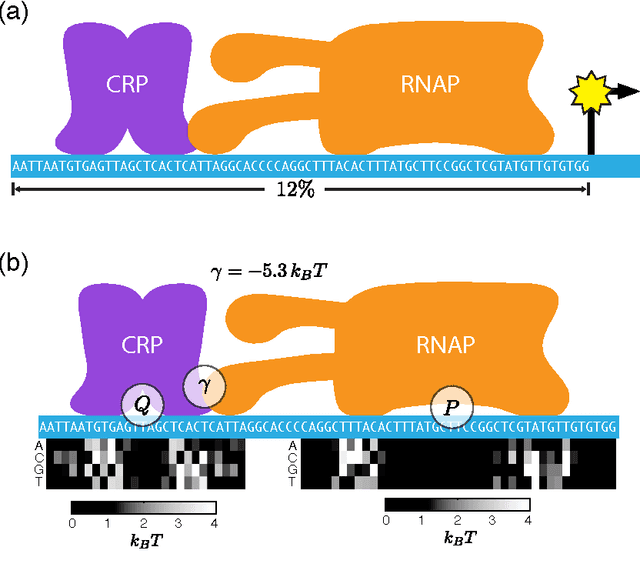
A fundamental aspect of biological information processing is the ubiquity of sequence-function relationships -- functions that map the sequence of DNA, RNA, or protein to a biochemically relevant activity. Most sequence-function relationships in biology are quantitative, but only recently have experimental techniques for effectively measuring these relationships been developed. The advent of such "massively parallel" experiments presents an exciting opportunity for the concepts and methods of statistical physics to inform the study of biological systems. After reviewing these recent experimental advances, we focus on the problem of how to infer parametric models of sequence-function relationships from the data produced by these experiments. Specifically, we retrace and extend recent theoretical work showing that inference based on mutual information, not the standard likelihood-based approach, is often necessary for accurately learning the parameters of these models. Closely connected with this result is the emergence of "diffeomorphic modes" -- directions in parameter space that are far less constrained by data than likelihood-based inference would suggest. Analogous to Goldstone modes in physics, diffeomorphic modes arise from an arbitrarily broken symmetry of the inference problem. An analytically tractable model of a massively parallel experiment is then described, providing an explicit demonstration of these fundamental aspects of statistical inference. This paper concludes with an outlook on the theoretical and computational challenges currently facing studies of quantitative sequence-function relationships.

Unification of field theory and maximum entropy methods for learning probability densities

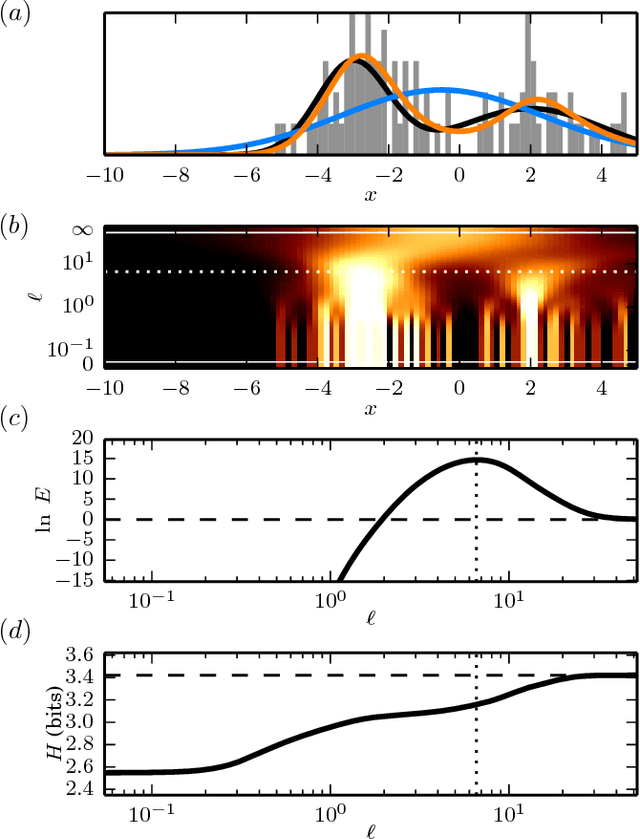
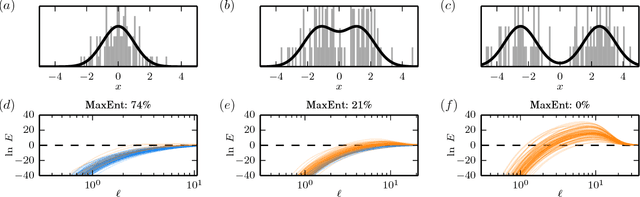
The need to estimate smooth probability distributions (a.k.a. probability densities) from finite sampled data is ubiquitous in science. Many approaches to this problem have been described, but none is yet regarded as providing a definitive solution. Maximum entropy estimation and Bayesian field theory are two such approaches. Both have origins in statistical physics, but the relationship between them has remained unclear. Here I unify these two methods by showing that every maximum entropy density estimate can be recovered in the infinite smoothness limit of an appropriate Bayesian field theory. I also show that Bayesian field theory estimation can be performed without imposing any boundary conditions on candidate densities, and that the infinite smoothness limit of these theories recovers the most common types of maximum entropy estimates. Bayesian field theory is thus seen to provide a natural test of the validity of the maximum entropy null hypothesis. Bayesian field theory also returns a lower entropy density estimate when the maximum entropy hypothesis is falsified. The computations necessary for this approach can be performed rapidly for one-dimensional data, and software for doing this is provided. Based on these results, I argue that Bayesian field theory is poised to provide a definitive solution to the density estimation problem in one dimension.

Rapid and deterministic estimation of probability densities using scale-free field theories

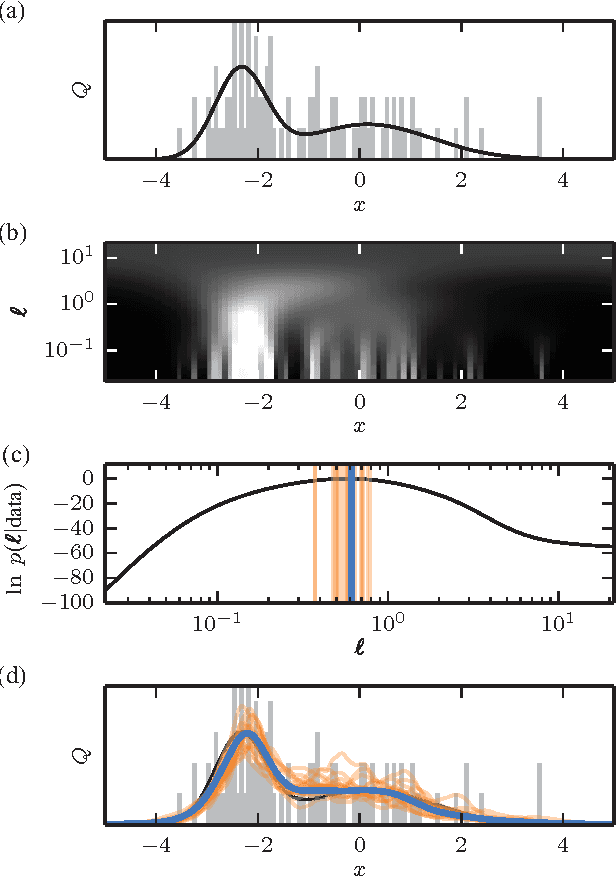
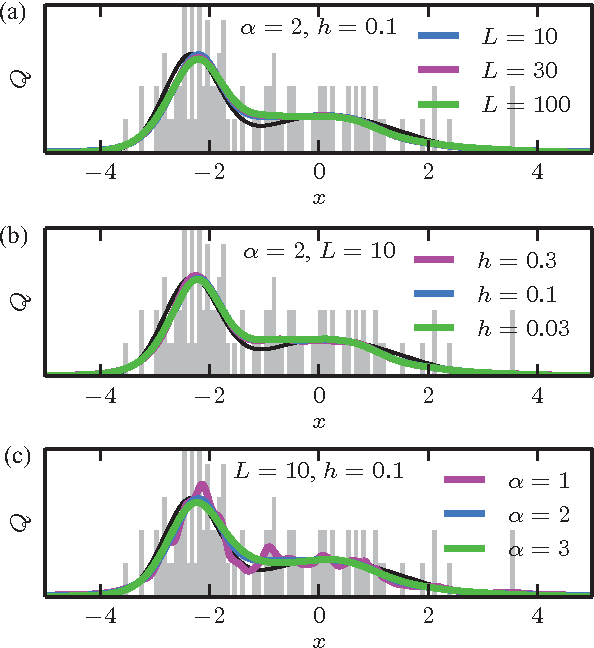
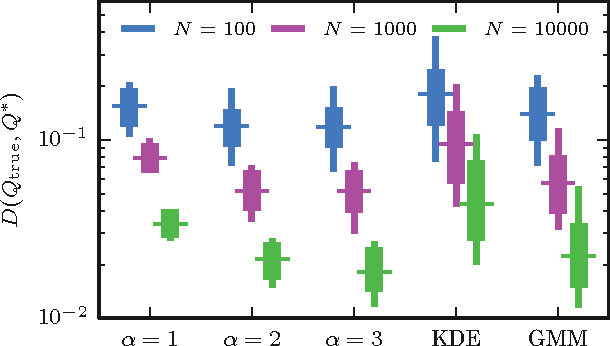
The question of how best to estimate a continuous probability density from finite data is an intriguing open problem at the interface of statistics and physics. Previous work has argued that this problem can be addressed in a natural way using methods from statistical field theory. Here I describe new results that allow this field-theoretic approach to be rapidly and deterministically computed in low dimensions, making it practical for use in day-to-day data analysis. Importantly, this approach does not impose a privileged length scale for smoothness of the inferred probability density, but rather learns a natural length scale from the data due to the tradeoff between goodness-of-fit and an Occam factor. Open source software implementing this method in one and two dimensions is provided.

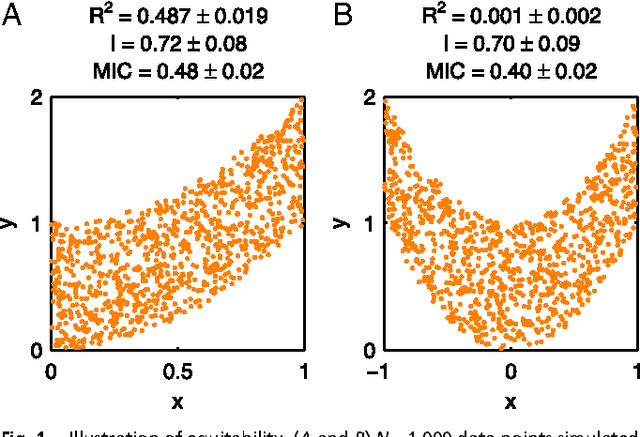
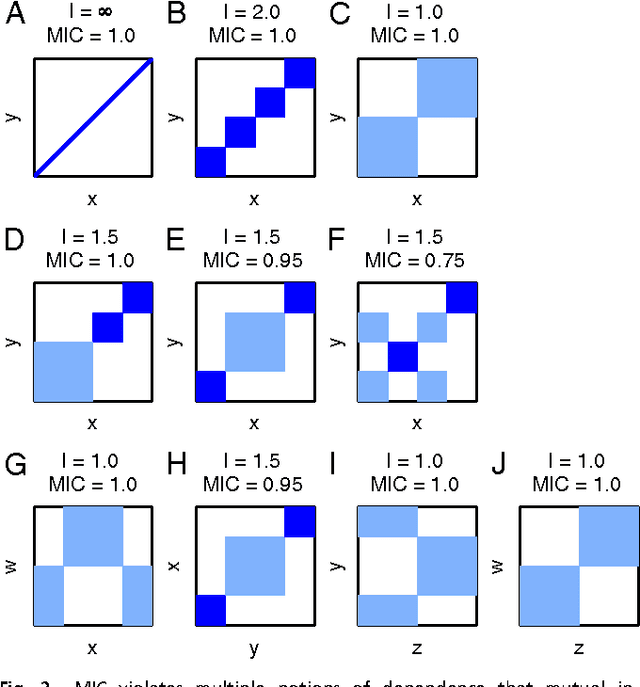
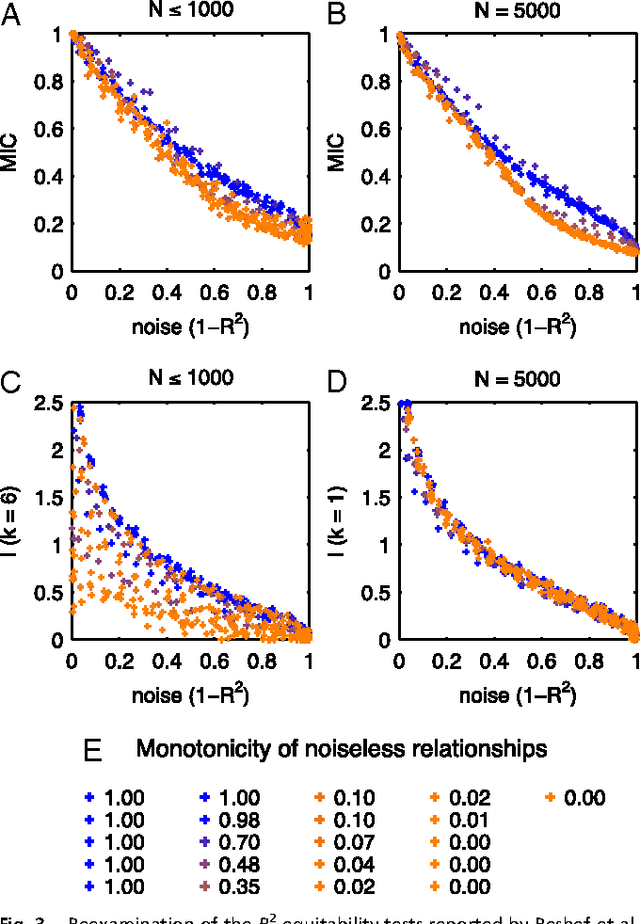
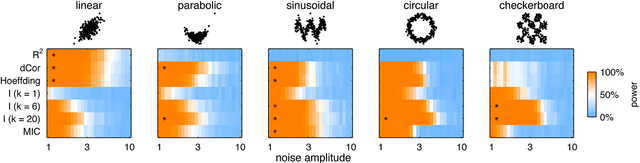
Equitability, mutual information, and the maximal information coefficient

Reshef et al. recently proposed a new statistical measure, the "maximal information coefficient" (MIC), for quantifying arbitrary dependencies between pairs of stochastic quantities. MIC is based on mutual information, a fundamental quantity in information theory that is widely understood to serve this need. MIC, however, is not an estimate of mutual information. Indeed, it was claimed that MIC possesses a desirable mathematical property called "equitability" that mutual information lacks. This was not proven; instead it was argued solely through the analysis of simulated data. Here we show that this claim, in fact, is incorrect. First we offer mathematical proof that no (non-trivial) dependence measure satisfies the definition of equitability proposed by Reshef et al.. We then propose a self-consistent and more general definition of equitability that follows naturally from the Data Processing Inequality. Mutual information satisfies this new definition of equitability while MIC does not. Finally, we show that the simulation evidence offered by Reshef et al. was artifactual. We conclude that estimating mutual information is not only practical for many real-world applications, but also provides a natural solution to the problem of quantifying associations in large data sets.