Learning Bayesian and Markov Networks with an Unreliable Oracle

We study constraint-based structure learning of Markov networks and Bayesian networks in the presence of an unreliable conditional independence oracle that makes at most a bounded number of errors. For Markov networks, we observe that a low maximum number of vertex-wise disjoint paths implies that the structure is uniquely identifiable even if the number of errors is (moderately) exponential in the number of vertices. For Bayesian networks, however, we prove that one cannot tolerate any errors to always identify the structure even when many commonly used graph parameters like treewidth are bounded. Finally, we give algorithms for structure learning when the structure is uniquely identifiable.

Improving Decision Trees through the Lens of Parameterized Local Search

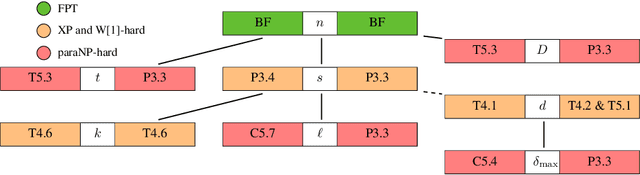
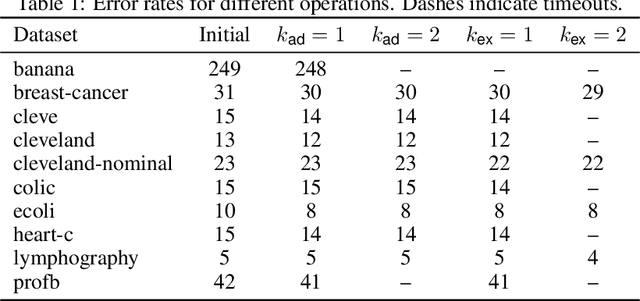
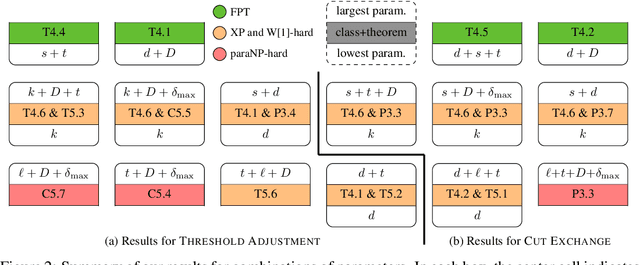
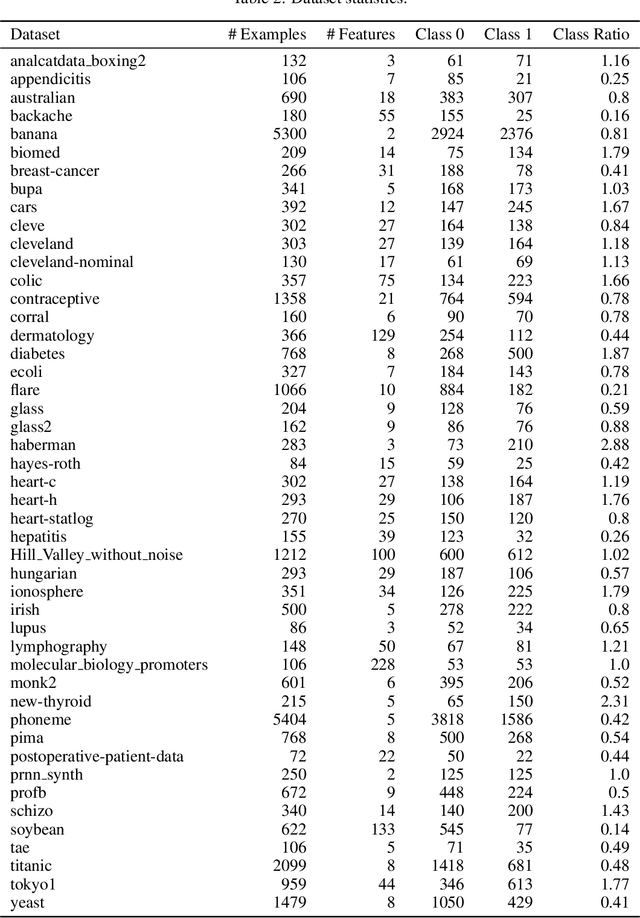
Algorithms for learning decision trees often include heuristic local-search operations such as (1) adjusting the threshold of a cut or (2) also exchanging the feature of that cut. We study minimizing the number of classification errors by performing a fixed number of a single type of these operations. Although we discover that the corresponding problems are NP-complete in general, we provide a comprehensive parameterized-complexity analysis with the aim of determining those properties of the problems that explain the hardness and those that make the problems tractable. For instance, we show that the problems remain hard for a small number $d$ of features or small domain size $D$ but the combination of both yields fixed-parameter tractability. That is, the problems are solvable in $(D + 1)^{2d} \cdot |I|^{O(1)}$ time, where $|I|$ is the size of the input. We also provide a proof-of-concept implementation of this algorithm and report on empirical results.

Optimal Decision Tree Pruning Revisited: Algorithms and Complexity

We present a comprehensive classical and parameterized complexity analysis of decision tree pruning operations, extending recent research on the complexity of learning small decision trees. Thereby, we offer new insights into the computational challenges of decision tree simplification, a crucial aspect of developing interpretable and efficient machine learning models. We focus on fundamental pruning operations of subtree replacement and raising, which are used in heuristics. Surprisingly, while optimal pruning can be performed in polynomial time for subtree replacement, the problem is NP-complete for subtree raising. Therefore, we identify parameters and combinations thereof that lead to fixed-parameter tractability or hardness, establishing a precise borderline between these complexity classes. For example, while subtree raising is hard for small domain size $D$ or number $d$ of features, it can be solved in $D^{2d} \cdot |I|^{O(1)}$ time, where $|I|$ is the input size. We complement our theoretical findings with preliminary experimental results, demonstrating the practical implications of our analysis.