Improving Decision Trees through the Lens of Parameterized Local Search
Paper and Code
Oct 14, 2025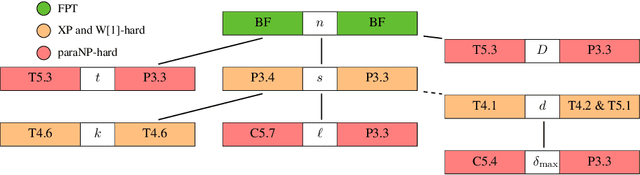
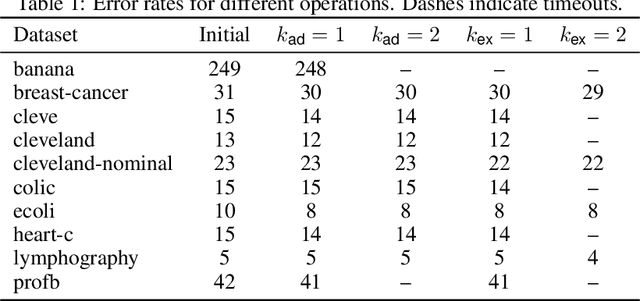
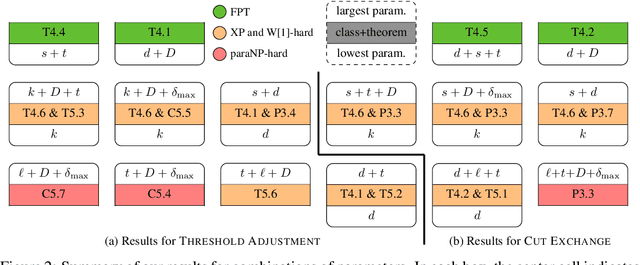
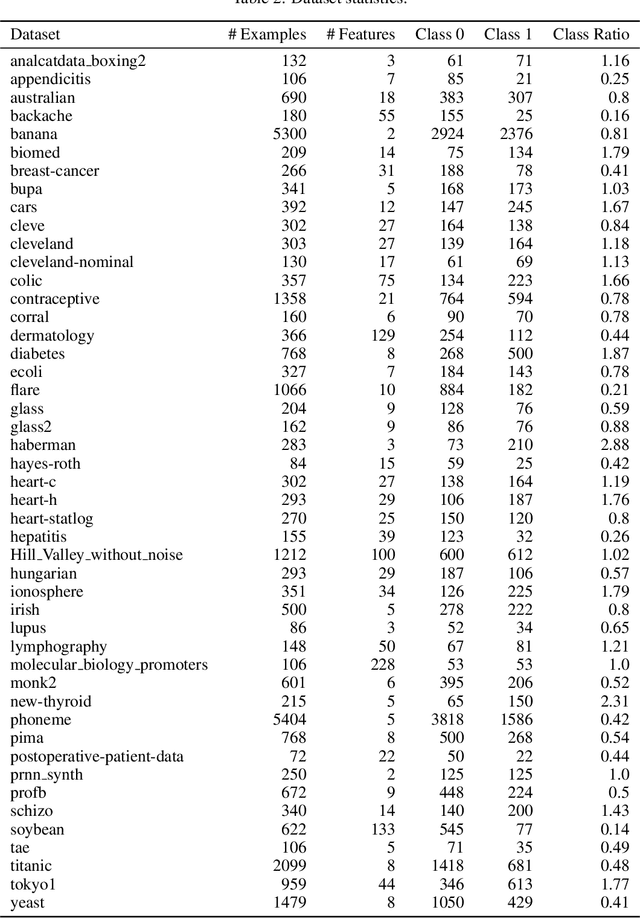
Algorithms for learning decision trees often include heuristic local-search operations such as (1) adjusting the threshold of a cut or (2) also exchanging the feature of that cut. We study minimizing the number of classification errors by performing a fixed number of a single type of these operations. Although we discover that the corresponding problems are NP-complete in general, we provide a comprehensive parameterized-complexity analysis with the aim of determining those properties of the problems that explain the hardness and those that make the problems tractable. For instance, we show that the problems remain hard for a small number $d$ of features or small domain size $D$ but the combination of both yields fixed-parameter tractability. That is, the problems are solvable in $(D + 1)^{2d} \cdot |I|^{O(1)}$ time, where $|I|$ is the size of the input. We also provide a proof-of-concept implementation of this algorithm and report on empirical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge