RandomOut: Using a convolutional gradient norm to rescue convolutional filters

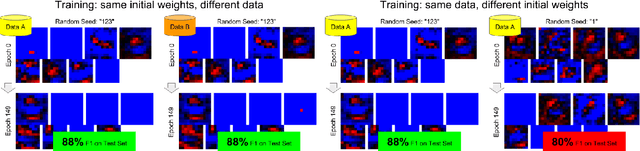
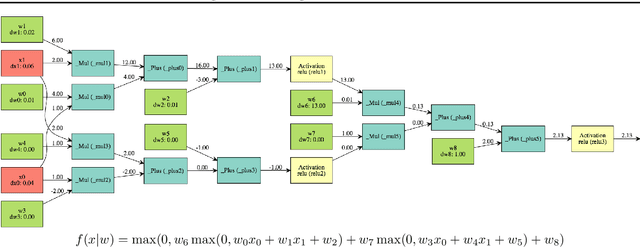
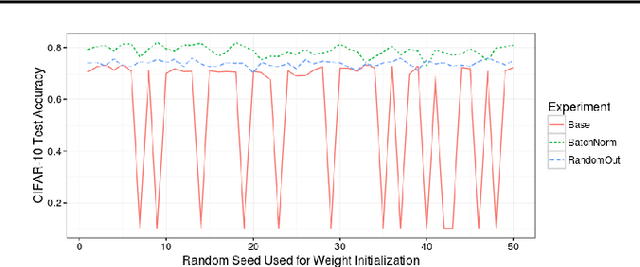
Filters in convolutional neural networks are sensitive to their initialization. The random numbers used to initialize filters are a bias and determine if you will "win" and converge to a satisfactory local minimum so we call this The Filter Lottery. We observe that the 28x28 Inception-V3 model without Batch Normalization fails to train 26% of the time when varying the random seed alone. This is a problem that affects the trial and error process of designing a network. Because random seeds have a large impact it makes it hard to evaluate a network design without trying many different random starting weights. This work aims to reduce the bias imposed by the initial weights so a network converges more consistently. We propose to evaluate and replace specific convolutional filters that have little impact on the prediction. We use the gradient norm to evaluate the impact of a filter on error, and re-initialize filters when the gradient norm of its weights falls below a specific threshold. This consistently improves accuracy on the 28x28 Inception-V3 with a median increase of +3.3%. In effect our method RandomOut increases the number of filters explored without increasing the size of the network. We observe that the RandomOut method has more consistent generalization performance, having a standard deviation of 1.3% instead of 2% when varying random seeds, and does so faster and with fewer parameters.

Rapid building detection using machine learning

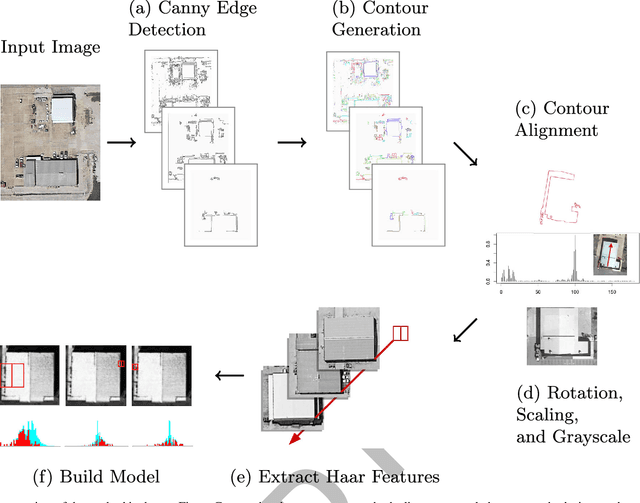
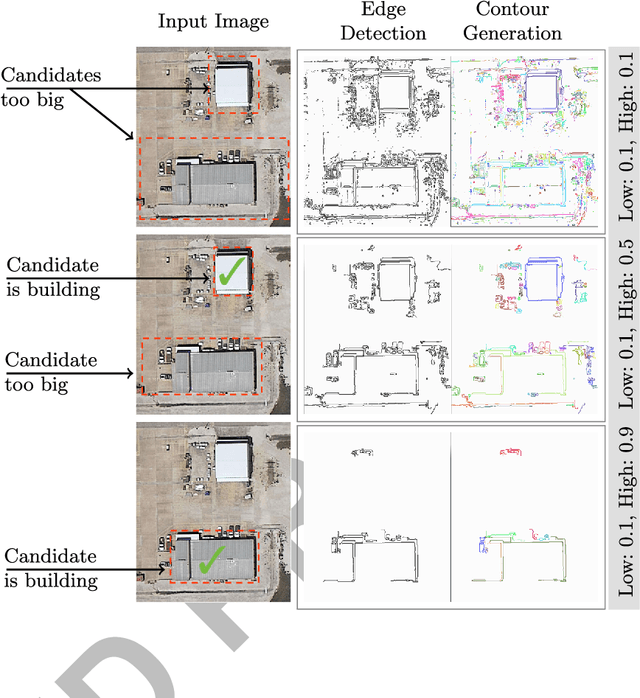
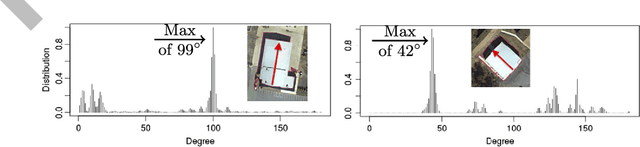
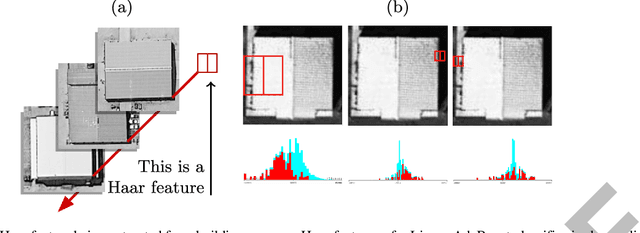
This work describes algorithms for performing discrete object detection, specifically in the case of buildings, where usually only low quality RGB-only geospatial reflective imagery is available. We utilize new candidate search and feature extraction techniques to reduce the problem to a machine learning (ML) classification task. Here we can harness the complex patterns of contrast features contained in training data to establish a model of buildings. We avoid costly sliding windows to generate candidates; instead we innovatively stitch together well known image processing techniques to produce candidates for building detection that cover 80-85% of buildings. Reducing the number of possible candidates is important due to the scale of the problem. Each candidate is subjected to classification which, although linear, costs time and prohibits large scale evaluation. We propose a candidate alignment algorithm to boost classification performance to 80-90% precision with a linear time algorithm and show it has negligible cost. Also, we propose a new concept called a Permutable Haar Mesh (PHM) which we use to form and traverse a search space to recover candidate buildings which were lost in the initial preprocessing phase.

Crater Detection via Convolutional Neural Networks

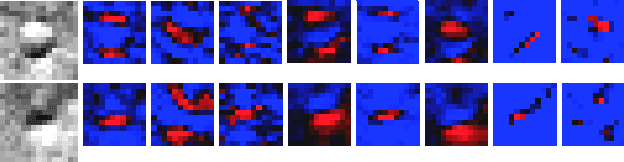
Craters are among the most studied geomorphic features in the Solar System because they yield important information about the past and present geological processes and provide information about the relative ages of observed geologic formations. We present a method for automatic crater detection using advanced machine learning to deal with the large amount of satellite imagery collected. The challenge of automatically detecting craters comes from their is complex surface because their shape erodes over time to blend into the surface. Bandeira provided a seminal dataset that embodied this challenge that is still an unsolved pattern recognition problem to this day. There has been work to solve this challenge based on extracting shape and contrast features and then applying classification models on those features. The limiting factor in this existing work is the use of hand crafted filters on the image such as Gabor or Sobel filters or Haar features. These hand crafted methods rely on domain knowledge to construct. We would like to learn the optimal filters and features based on training examples. In order to dynamically learn filters and features we look to Convolutional Neural Networks (CNNs) which have shown their dominance in computer vision. The power of CNNs is that they can learn image filters which generate features for high accuracy classification.