Quantifying Model Uncertainty for Semantic Segmentation using Operators in the RKHS

Deep learning models for semantic segmentation are prone to poor performance in real-world applications due to the highly challenging nature of the task. Model uncertainty quantification (UQ) is one way to address this issue of lack of model trustworthiness by enabling the practitioner to know how much to trust a segmentation output. Current UQ methods in this application domain are mainly restricted to Bayesian based methods which are computationally expensive and are only able to extract central moments of uncertainty thereby limiting the quality of their uncertainty estimates. We present a simple framework for high-resolution predictive uncertainty quantification of semantic segmentation models that leverages a multi-moment functional definition of uncertainty associated with the model's feature space in the reproducing kernel Hilbert space (RKHS). The multiple uncertainty functionals extracted from this framework are defined by the local density dynamics of the model's feature space and hence automatically align themselves at the tail-regions of the intrinsic probability density function of the feature space (where uncertainty is the highest) in such a way that the successively higher order moments quantify the more uncertain regions. This leads to a significantly more accurate view of model uncertainty than conventional Bayesian methods. Moreover, the extraction of such moments is done in a single-shot computation making it much faster than Bayesian and ensemble approaches (that involve a high number of forward stochastic passes of the model to quantify its uncertainty). We demonstrate these advantages through experimental evaluations of our framework implemented over four different state-of-the-art model architectures that are trained and evaluated on two benchmark road-scene segmentation datasets (Camvid and Cityscapes).

Principle of Relevant Information for Graph Sparsification

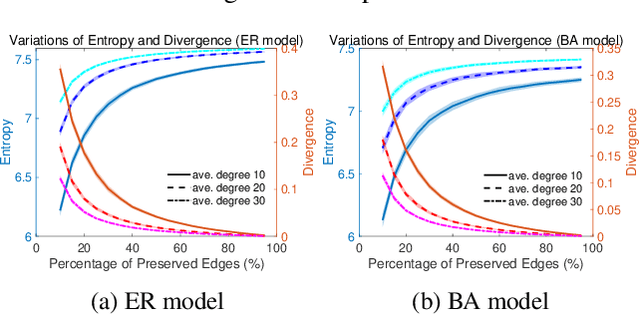
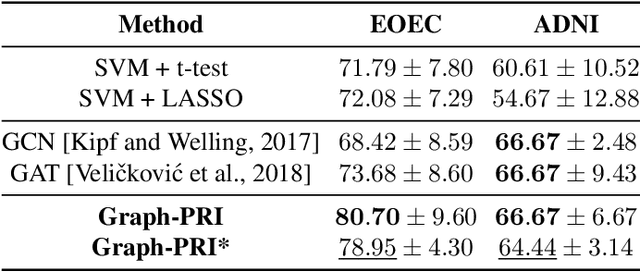
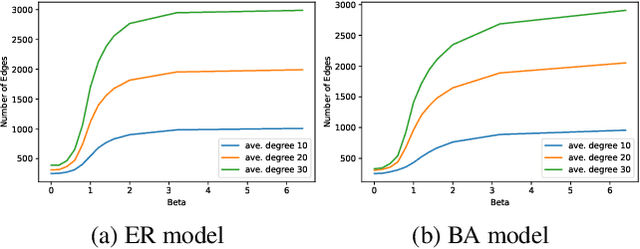
Graph sparsification aims to reduce the number of edges of a graph while maintaining its structural properties. In this paper, we propose the first general and effective information-theoretic formulation of graph sparsification, by taking inspiration from the Principle of Relevant Information (PRI). To this end, we extend the PRI from a standard scalar random variable setting to structured data (i.e., graphs). Our Graph-PRI objective is achieved by operating on the graph Laplacian, made possible by expressing the graph Laplacian of a subgraph in terms of a sparse edge selection vector $\mathbf{w}$. We provide both theoretical and empirical justifications on the validity of our Graph-PRI approach. We also analyze its analytical solutions in a few special cases. We finally present three representative real-world applications, namely graph sparsification, graph regularized multi-task learning, and medical imaging-derived brain network classification, to demonstrate the effectiveness, the versatility and the enhanced interpretability of our approach over prevalent sparsification techniques. Code of Graph-PRI is available at https://github.com/SJYuCNEL/PRI-Graphs

Deep Deterministic Independent Component Analysis for Hyperspectral Unmixing

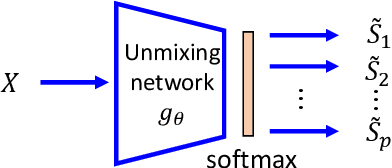
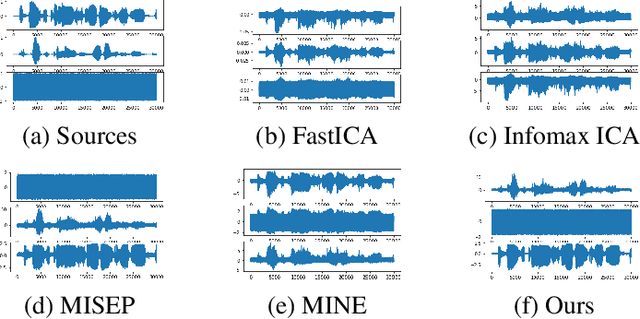
We develop a new neural network based independent component analysis (ICA) method by directly minimizing the dependence amongst all extracted components. Using the matrix-based R{\'e}nyi's $\alpha$-order entropy functional, our network can be directly optimized by stochastic gradient descent (SGD), without any variational approximation or adversarial training. As a solid application, we evaluate our ICA in the problem of hyperspectral unmixing (HU) and refute a statement that "\emph{ICA does not play a role in unmixing hyperspectral data}", which was initially suggested by \cite{nascimento2005does}. Code and additional remarks of our DDICA is available at https://github.com/hongmingli1995/DDICA.

Information Theoretic Structured Generative Modeling

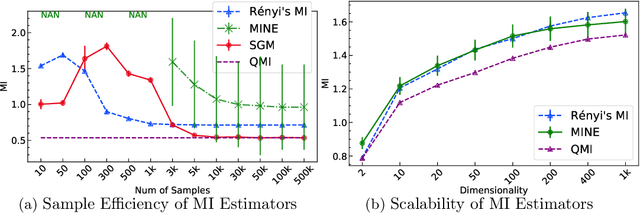
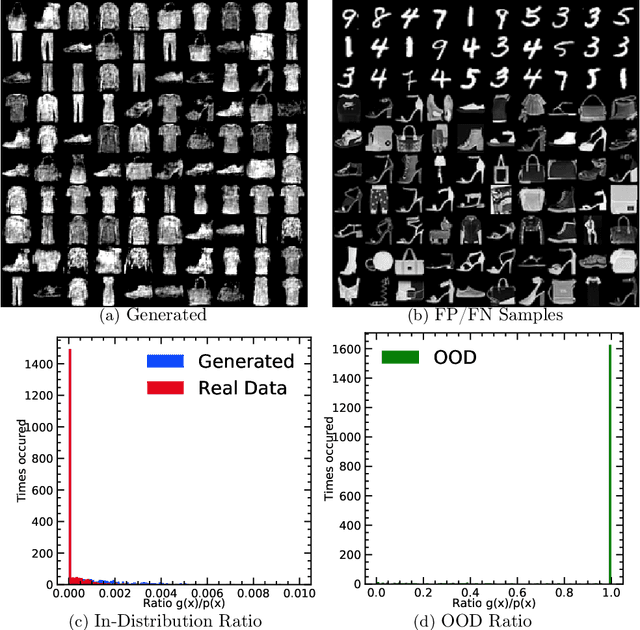
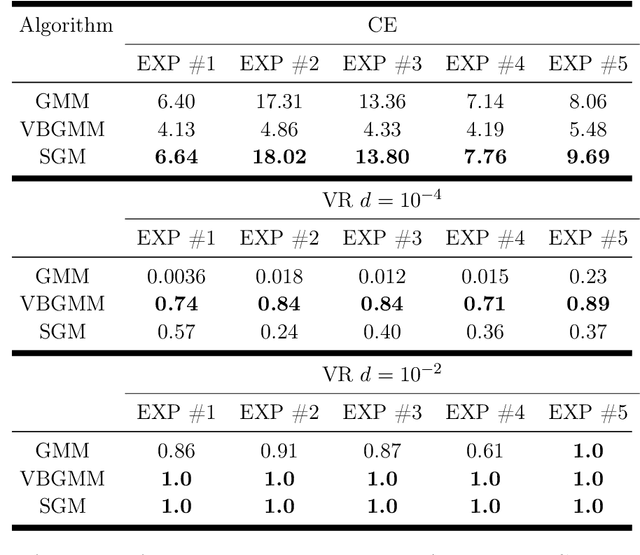
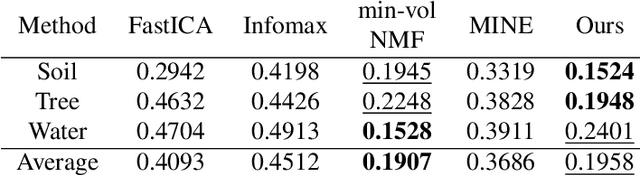
R\'enyi's information provides a theoretical foundation for tractable and data-efficient non-parametric density estimation, based on pair-wise evaluations in a reproducing kernel Hilbert space (RKHS). This paper extends this framework to parametric probabilistic modeling, motivated by the fact that R\'enyi's information can be estimated in closed-form for Gaussian mixtures. Based on this special connection, a novel generative model framework called the structured generative model (SGM) is proposed that makes straightforward optimization possible, because costs are scale-invariant, avoiding high gradient variance while imposing less restrictions on absolute continuity, which is a huge advantage in parametric information theoretic optimization. The implementation employs a single neural network driven by an orthonormal input appended to a single white noise source adapted to learn an infinite Gaussian mixture model (IMoG), which provides an empirically tractable model distribution in low dimensions. To train SGM, we provide three novel variational cost functions, based on R\'enyi's second-order entropy and divergence, to implement minimization of cross-entropy, minimization of variational representations of $f$-divergence, and maximization of the evidence lower bound (conditional probability). We test the framework for estimation of mutual information and compare the results with the mutual information neural estimation (MINE), for density estimation, for conditional probability estimation in Markov models as well as for training adversarial networks. Our preliminary results show that SGM significantly improves MINE estimation in terms of data efficiency and variance, conventional and variational Gaussian mixture models, as well as the performance of generative adversarial networks.

Estimating Rényi's $α$-Cross-Entropies in a Matrix-Based Way

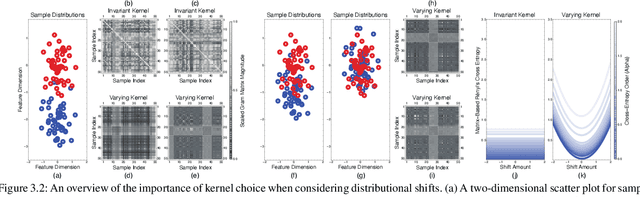
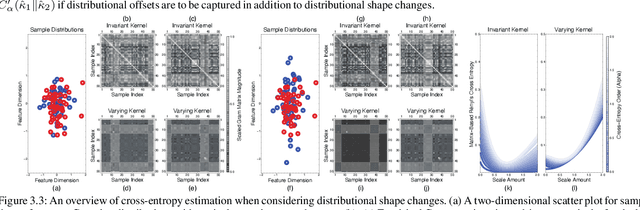
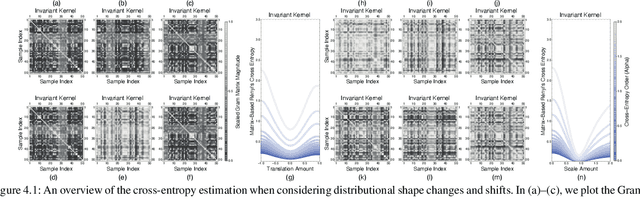
Conventional information-theoretic quantities assume access to probability distributions. Estimating such distributions is not trivial. Here, we consider function-based formulations of cross entropy that sidesteps this a priori estimation requirement. We propose three measures of R\'enyi's $\alpha$-cross-entropies in the setting of reproducing-kernel Hilbert spaces. Each measure has its appeals. We prove that we can estimate these measures in an unbiased, non-parametric, and minimax-optimal way. We do this via sample-constructed Gram matrices. This yields matrix-based estimators of R\'enyi's $\alpha$-cross-entropies. These estimators satisfy all of the axioms that R\'enyi established for divergences. Our cross-entropies can thus be used for assessing distributional differences. They are also appropriate for handling high-dimensional distributions, since the convergence rate of our estimator is independent of the sample dimensionality. Python code for implementing these measures can be found at https://github.com/isledge/MBRCE

Quantifying Model Predictive Uncertainty with Perturbation Theory

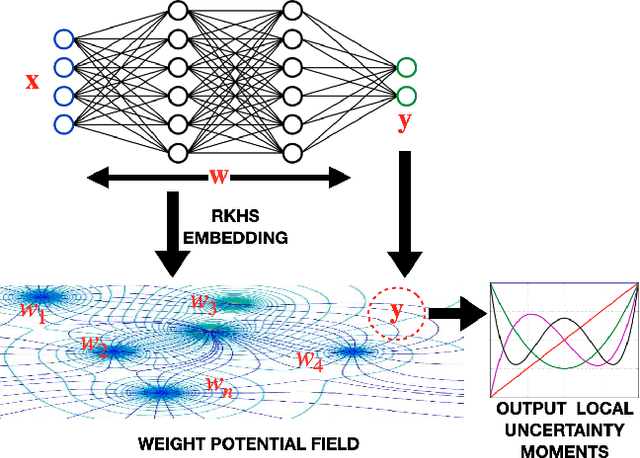
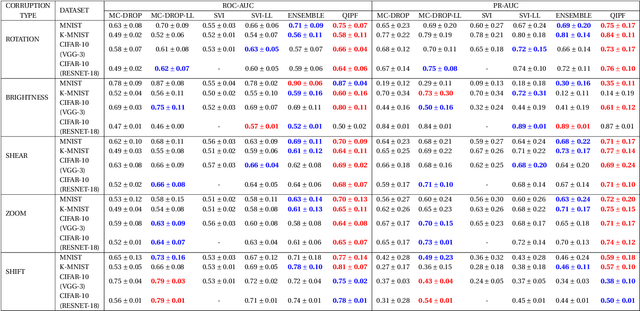
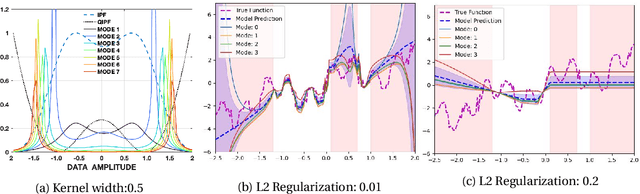
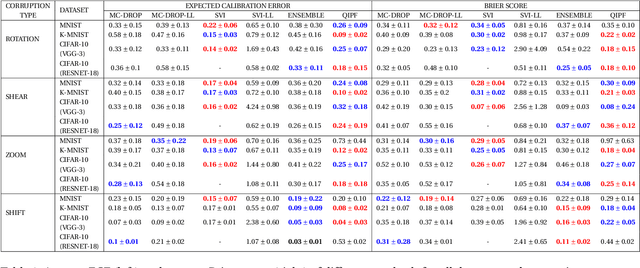
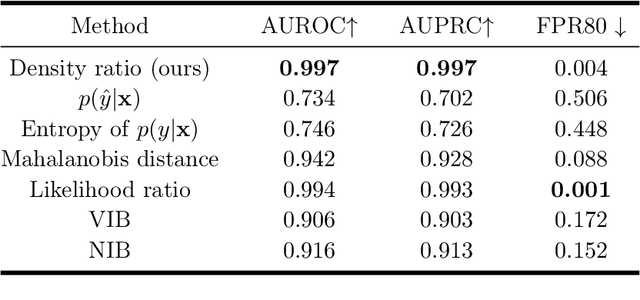
We propose a framework for predictive uncertainty quantification of a neural network that replaces the conventional Bayesian notion of weight probability density function (PDF) with a physics based potential field representation of the model weights in a Gaussian reproducing kernel Hilbert space (RKHS) embedding. This allows us to use perturbation theory from quantum physics to formulate a moment decomposition problem over the model weight-output relationship. The extracted moments reveal successive degrees of regularization of the weight potential field around the local neighborhood of the model output. Such localized moments represent well the PDF tails and provide significantly greater accuracy of the model's predictive uncertainty than the central moments characterized by Bayesian and ensemble methods or their variants. We show that this consequently leads to a better ability to detect false model predictions of test data that has undergone a covariate shift away from the training PDF learned by the model. We evaluate our approach against baseline uncertainty quantification methods on several benchmark datasets that are corrupted using common distortion techniques. Our approach provides fast model predictive uncertainty estimates with much greater precision and calibration.

Analysis of Intra-Operative Physiological Responses Through Complex Higher-Order SVD for Long-Term Post-Operative Pain Prediction

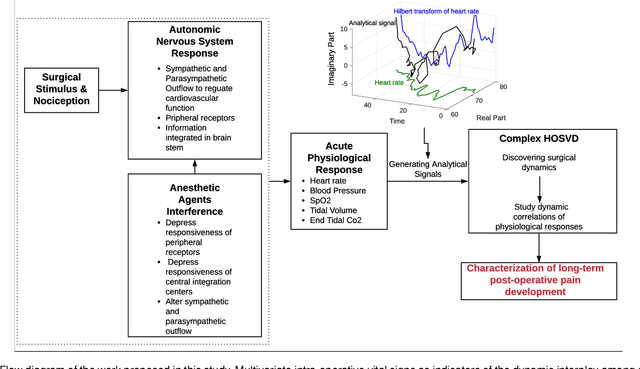
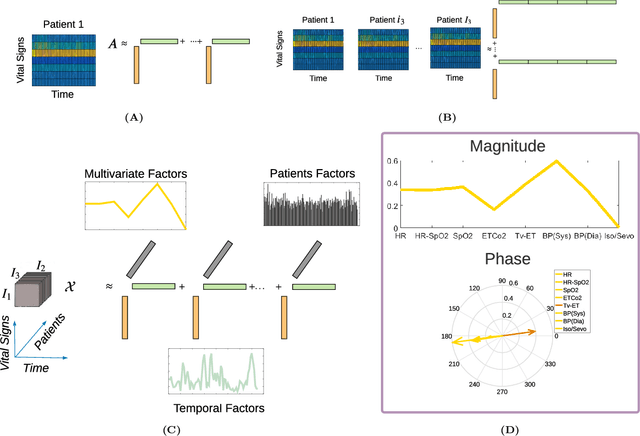
Long-term pain conditions after surgery and patients' responses to pain relief medications are not yet fully understood. While recent studies developed an index for nociception level of patients under general anesthesia, based on multiple physiological parameters, it remains unclear whether and how dynamics of these parameters indicate long-term post-operative pain (POP). To extract unbiased and interpretable descriptions of how physiological parameters dynamics change over time and across patients in response to surgical procedures, we employed a multivariate-temporal analysis. We demonstrate the main features of intra-operative physiological responses can be used to predict long-term POP. We propose to use a complex higher-order SVD method to accurately decompose the patients' physiological responses into multivariate structures evolving in time. We used intra-operative vital signs of 175 patients from a mixed surgical cohort to extract three interconnected, low-dimensional complex-valued descriptions of patients' physiological responses: multivariate factors, reflecting sub-physiological parameters; temporal factors reflecting common intra-surgery temporal dynamics; and patients factors, describing patient to patient changes in physiological responses. Adoption of complex-HOSVD allowed us to clarify the dynamic correlation structure included in intra-operative physiological responses. Instantaneous phases of the complex-valued physiological responses within the subspace of principal descriptors enabled us to discriminate between mild versus severe levels of long-term POP. By abstracting patients into different surgical groups, we identified significant surgery-related principal descriptors: each of them potentially encodes different surgical stimulation. The dynamics of patients' physiological responses to these surgical events are linked to long-term post-operative pain development.

External-Memory Networks for Low-Shot Learning of Targets in Forward-Looking-Sonar Imagery

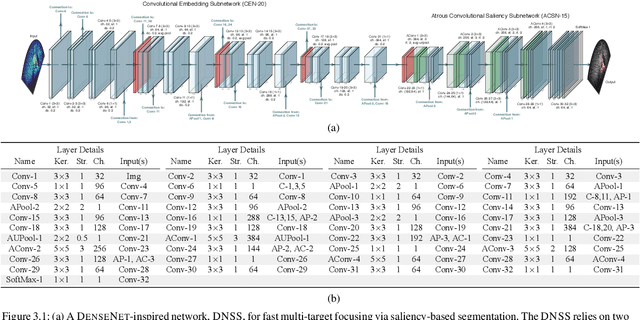
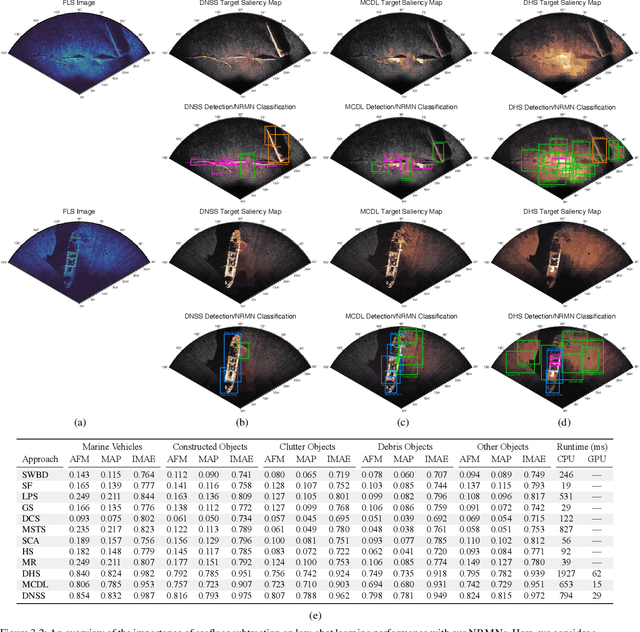
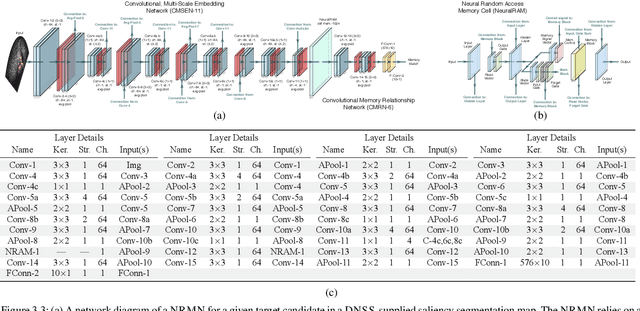
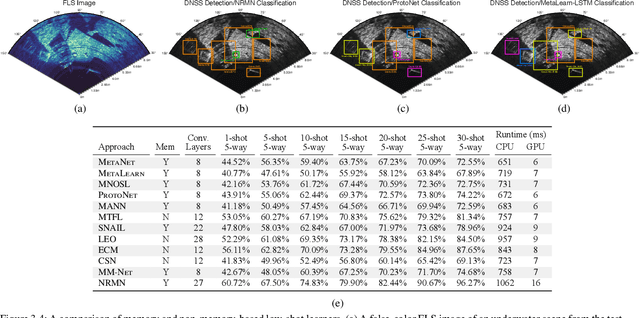
We propose a memory-based framework for real-time, data-efficient target analysis in forward-looking-sonar (FLS) imagery. Our framework relies on first removing non-discriminative details from the imagery using a small-scale DenseNet-inspired network. Doing so simplifies ensuing analyses and permits generalizing from few labeled examples. We then cascade the filtered imagery into a novel NeuralRAM-based convolutional matching network, NRMN, for low-shot target recognition. We employ a small-scale FlowNet, LFN to align and register FLS imagery across local temporal scales. LFN enables target label consensus voting across images and generally improves target detection and recognition rates. We evaluate our framework using real-world FLS imagery with multiple broad target classes that have high intra-class variability and rich sub-class structure. We show that few-shot learning, with anywhere from ten to thirty class-specific exemplars, performs similarly to supervised deep networks trained on hundreds of samples per class. Effective zero-shot learning is also possible. High performance is realized from the inductive-transfer properties of NRMNs when distractor elements are removed.

An Information-Theoretic Approach for Automatically Determining the Number of States when Aggregating Markov Chains

A fundamental problem when aggregating Markov chains is the specification of the number of state groups. Too few state groups may fail to sufficiently capture the pertinent dynamics of the original, high-order Markov chain. Too many state groups may lead to a non-parsimonious, reduced-order Markov chain whose complexity rivals that of the original. In this paper, we show that an augmented value-of-information-based approach to aggregating Markov chains facilitates the determination of the number of state groups. The optimal state-group count coincides with the case where the complexity of the reduced-order chain is balanced against the mutual dependence between the original- and reduced-order chain dynamics.

Labels, Information, and Computation: Efficient, Privacy-Preserving Learning Using Sufficient Labels

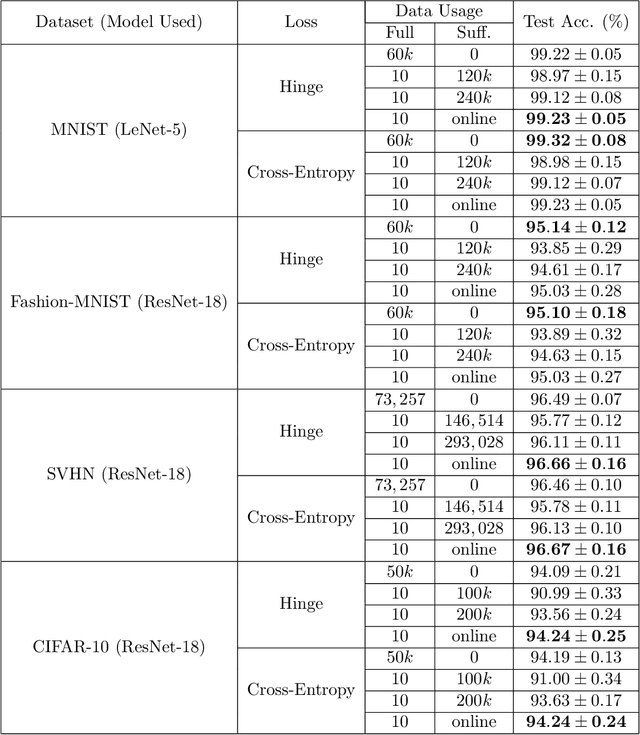
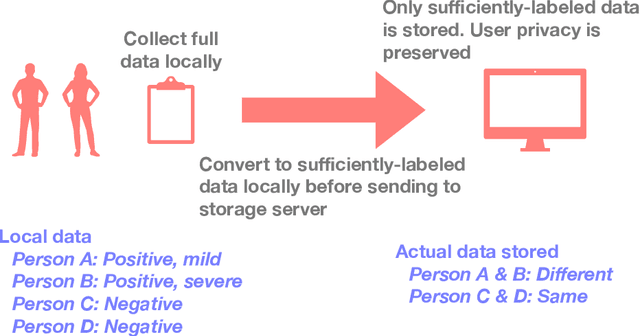
In supervised learning, obtaining a large set of fully-labeled training data is expensive. We show that we do not always need full label information on every single training example to train a competent classifier. Specifically, inspired by the principle of sufficiency in statistics, we present a statistic (a summary) of the fully-labeled training set that captures almost all the relevant information for classification but at the same time is easier to obtain directly. We call this statistic "sufficiently-labeled data" and prove its sufficiency and efficiency for finding the optimal hidden representations, on which competent classifier heads can be trained using as few as a single randomly-chosen fully-labeled example per class. Sufficiently-labeled data can be obtained from annotators directly without collecting the fully-labeled data first. And we prove that it is easier to directly obtain sufficiently-labeled data than obtaining fully-labeled data. Furthermore, sufficiently-labeled data naturally preserves user privacy by storing relative, instead of absolute, information. Extensive experimental results are provided to support our theory.