Learning Minimum Volume Sets and Anomaly Detectors from KNN Graphs

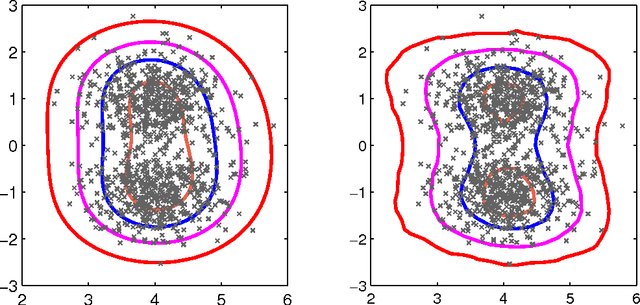
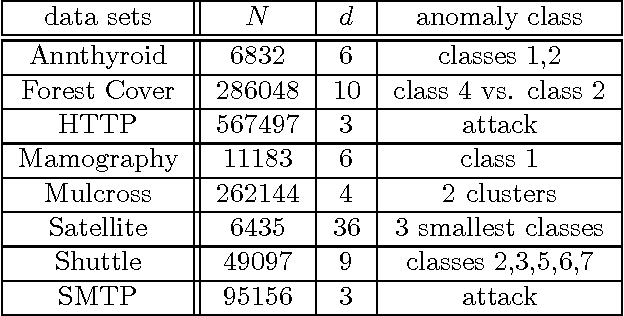
We propose a non-parametric anomaly detection algorithm for high dimensional data. We first rank scores derived from nearest neighbor graphs on $n$-point nominal training data. We then train limited complexity models to imitate these scores based on the max-margin learning-to-rank framework. A test-point is declared as an anomaly at $\alpha$-false alarm level if the predicted score is in the $\alpha$-percentile. The resulting anomaly detector is shown to be asymptotically optimal in that for any false alarm rate $\alpha$, its decision region converges to the $\alpha$-percentile minimum volume level set of the unknown underlying density. In addition, we test both the statistical performance and computational efficiency of our algorithm on a number of synthetic and real-data experiments. Our results demonstrate the superiority of our algorithm over existing $K$-NN based anomaly detection algorithms, with significant computational savings.

Learning Efficient Anomaly Detectors from $K$-NN Graphs

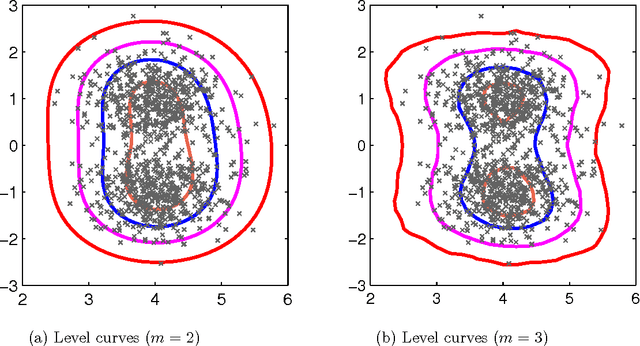
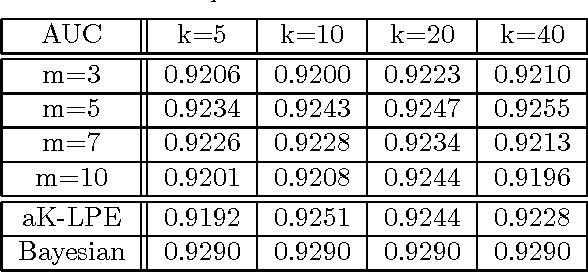
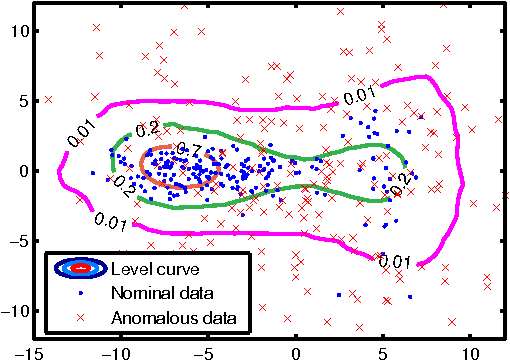
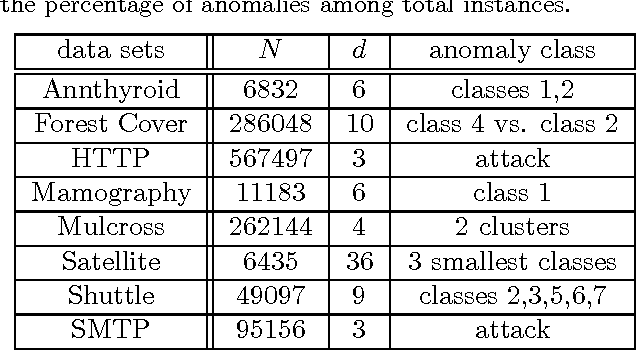
We propose a non-parametric anomaly detection algorithm for high dimensional data. We score each datapoint by its average $K$-NN distance, and rank them accordingly. We then train limited complexity models to imitate these scores based on the max-margin learning-to-rank framework. A test-point is declared as an anomaly at $\alpha$-false alarm level if the predicted score is in the $\alpha$-percentile. The resulting anomaly detector is shown to be asymptotically optimal in that for any false alarm rate $\alpha$, its decision region converges to the $\alpha$-percentile minimum volume level set of the unknown underlying density. In addition, we test both the statistical performance and computational efficiency of our algorithm on a number of synthetic and real-data experiments. Our results demonstrate the superiority of our algorithm over existing $K$-NN based anomaly detection algorithms, with significant computational savings.

A Rank-SVM Approach to Anomaly Detection

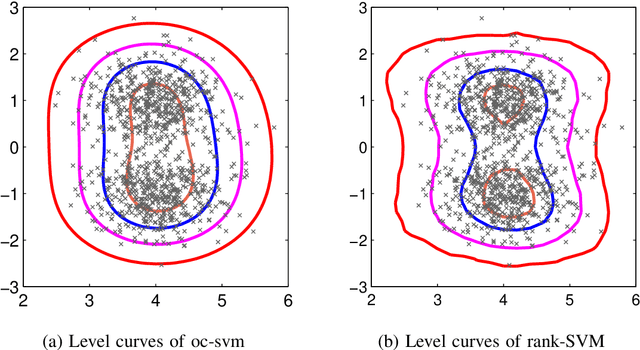
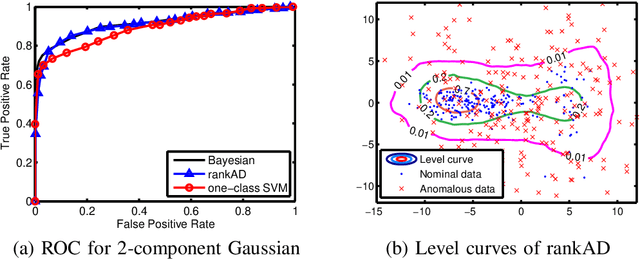
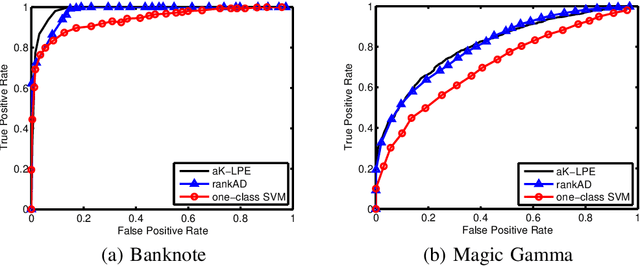
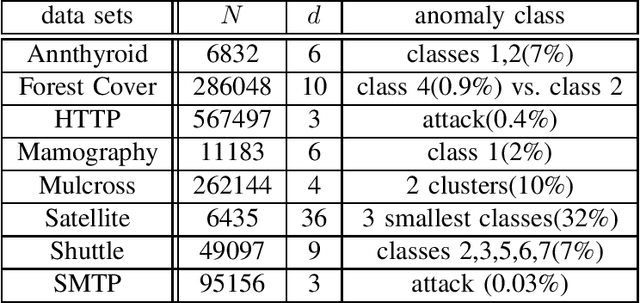
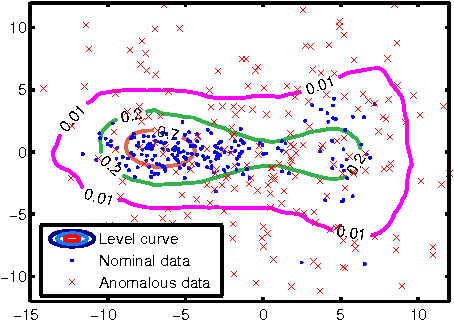
We propose a novel non-parametric adaptive anomaly detection algorithm for high dimensional data based on rank-SVM. Data points are first ranked based on scores derived from nearest neighbor graphs on n-point nominal data. We then train a rank-SVM using this ranked data. A test-point is declared as an anomaly at alpha-false alarm level if the predicted score is in the alpha-percentile. The resulting anomaly detector is shown to be asymptotically optimal and adaptive in that for any false alarm rate alpha, its decision region converges to the alpha-percentile level set of the unknown underlying density. In addition we illustrate through a number of synthetic and real-data experiments both the statistical performance and computational efficiency of our anomaly detector.