Reinforcement Learning From State and Temporal Differences

TD($λ$) with function approximation has proved empirically successful for some complex reinforcement learning problems. For linear approximation, TD($λ$) has been shown to minimise the squared error between the approximate value of each state and the true value. However, as far as policy is concerned, it is error in the relative ordering of states that is critical, rather than error in the state values. We illustrate this point, both in simple two-state and three-state systems in which TD($λ$)--starting from an optimal policy--converges to a sub-optimal policy, and also in backgammon. We then present a modified form of TD($λ$), called STD($λ$), in which function approximators are trained with respect to relative state values on binary decision problems. A theoretical analysis, including a proof of monotonic policy improvement for STD($λ$) in the context of the two-state system, is presented, along with a comparison with Bertsekas' differential training method [1]. This is followed by successful demonstrations of STD($λ$) on the two-state system and a variation on the well known acrobot problem.

Theoretical Models of Learning to Learn

A Machine can only learn if it is biased in some way. Typically the bias is supplied by hand, for example through the choice of an appropriate set of features. However, if the learning machine is embedded within an {\em environment} of related tasks, then it can {\em learn} its own bias by learning sufficiently many tasks from the environment. In this paper two models of bias learning (or equivalently, learning to learn) are introduced and the main theoretical results presented. The first model is a PAC-type model based on empirical process theory, while the second is a hierarchical Bayes model.

Learning Internal Representations (COLT 1995)

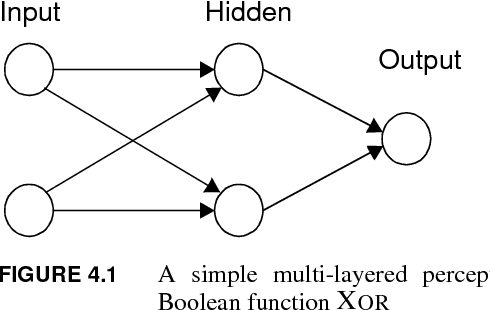
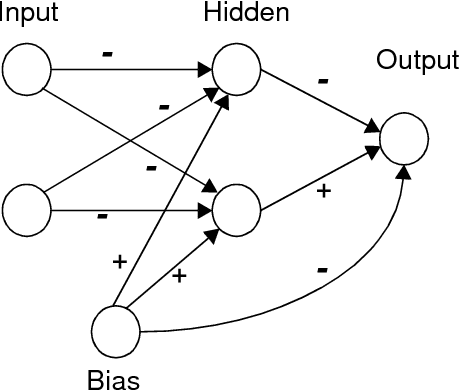
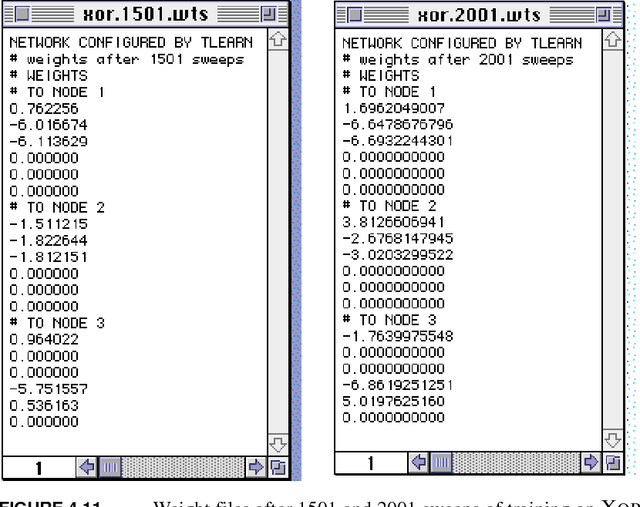
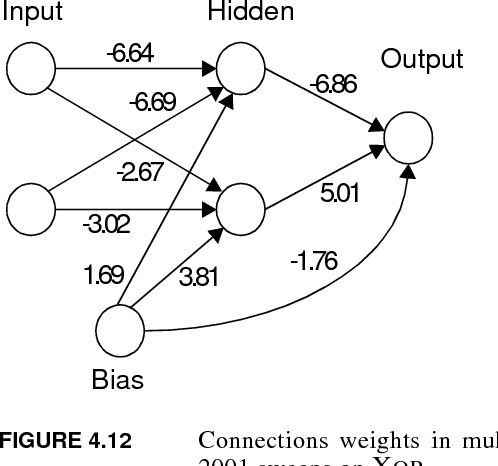
Probably the most important problem in machine learning is the preliminary biasing of a learner's hypothesis space so that it is small enough to ensure good generalisation from reasonable training sets, yet large enough that it contains a good solution to the problem being learnt. In this paper a mechanism for {\em automatically} learning or biasing the learner's hypothesis space is introduced. It works by first learning an appropriate {\em internal representation} for a learning environment and then using that representation to bias the learner's hypothesis space for the learning of future tasks drawn from the same environment. An internal representation must be learnt by sampling from {\em many similar tasks}, not just a single task as occurs in ordinary machine learning. It is proved that the number of examples $m$ {\em per task} required to ensure good generalisation from a representation learner obeys $m = O(a+b/n)$ where $n$ is the number of tasks being learnt and $a$ and $b$ are constants. If the tasks are learnt independently ({\em i.e.} without a common representation) then $m=O(a+b)$. It is argued that for learning environments such as speech and character recognition $b\gg a$ and hence representation learning in these environments can potentially yield a drastic reduction in the number of examples required per task. It is also proved that if $n = O(b)$ (with $m=O(a+b/n)$) then the representation learnt will be good for learning novel tasks from the same environment, and that the number of examples required to generalise well on a novel task will be reduced to $O(a)$ (as opposed to $O(a+b)$ if no representation is used). It is shown that gradient descent can be used to train neural network representations and experiment results are reported providing strong qualitative support for the theoretical results.

Learning Internal Representations

Most machine learning theory and practice is concerned with learning a single task. In this thesis it is argued that in general there is insufficient information in a single task for a learner to generalise well and that what is required for good generalisation is information about many similar learning tasks. Similar learning tasks form a body of prior information that can be used to constrain the learner and make it generalise better. Examples of learning scenarios in which there are many similar tasks are handwritten character recognition and spoken word recognition. The concept of the environment of a learner is introduced as a probability measure over the set of learning problems the learner might be expected to learn. It is shown how a sample from the environment may be used to learn a representation, or recoding of the input space that is appropriate for the environment. Learning a representation can equivalently be thought of as learning the appropriate features of the environment. Bounds are derived on the sample size required to ensure good generalisation from a representation learning process. These bounds show that under certain circumstances learning a representation appropriate for $n$ tasks reduces the number of examples required of each task by a factor of $n$. Once a representation is learnt it can be used to learn novel tasks from the same environment, with the result that far fewer examples are required of the new tasks to ensure good generalisation. Bounds are given on the number of tasks and the number of samples from each task required to ensure that a representation will be a good one for learning novel tasks. The results on representation learning are generalised to cover any form of automated hypothesis space bias.

General Matrix-Matrix Multiplication Using SIMD features of the PIII

Generalised matrix-matrix multiplication forms the kernel of many mathematical algorithms. A faster matrix-matrix multiply immediately benefits these algorithms. In this paper we implement efficient matrix multiplication for large matrices using the floating point Intel Pentium SIMD (Single Instruction Multiple Data) architecture. A description of the issues and our solution is presented, paying attention to all levels of the memory hierarchy. Our results demonstrate an average performance of 2.09 times faster than the leading public domain matrix-matrix multiply routines.

Some observations concerning Off Training Set (OTS) error

A form of generalisation error known as Off Training Set (OTS) error was recently introduced in [Wolpert, 1996b], along with a theorem showing that small training set error does not guarantee small OTS error, unless assumptions are made about the target function. Here it is shown that the applicability of this theorem is limited to models in which the distribution generating training data has no overlap with the distribution generating test data. It is argued that such a scenario is of limited relevance to machine learning.

Hebbian Synaptic Modifications in Spiking Neurons that Learn

In this paper, we derive a new model of synaptic plasticity, based on recent algorithms for reinforcement learning (in which an agent attempts to learn appropriate actions to maximize its long-term average reward). We show that these direct reinforcement learning algorithms also give locally optimal performance for the problem of reinforcement learning with multiple agents, without any explicit communication between agents. By considering a network of spiking neurons as a collection of agents attempting to maximize the long-term average of a reward signal, we derive a synaptic update rule that is qualitatively similar to Hebb's postulate. This rule requires only simple computations, such as addition and leaky integration, and involves only quantities that are available in the vicinity of the synapse. Furthermore, it leads to synaptic connection strengths that give locally optimal values of the long term average reward. The reinforcement learning paradigm is sufficiently broad to encompass many learning problems that are solved by the brain. We illustrate, with simulations, that the approach is effective for simple pattern classification and motor learning tasks.

The Canonical Distortion Measure for Vector Quantization and Function Approximation

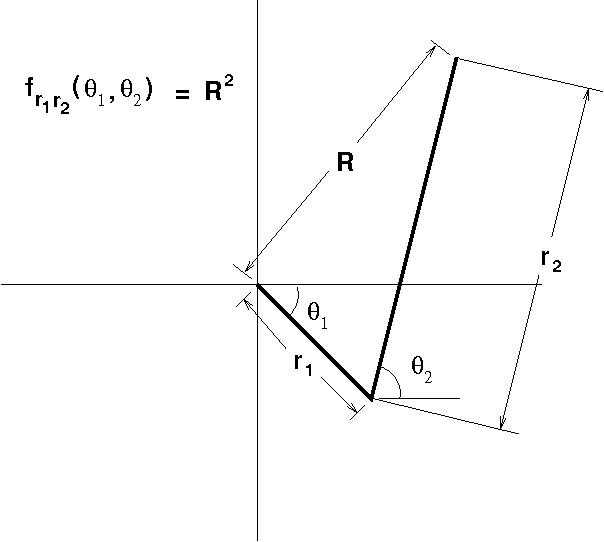
To measure the quality of a set of vector quantization points a means of measuring the distance between a random point and its quantization is required. Common metrics such as the {\em Hamming} and {\em Euclidean} metrics, while mathematically simple, are inappropriate for comparing natural signals such as speech or images. In this paper it is shown how an {\em environment} of functions on an input space $X$ induces a {\em canonical distortion measure} (CDM) on X. The depiction 'canonical" is justified because it is shown that optimizing the reconstruction error of X with respect to the CDM gives rise to optimal piecewise constant approximations of the functions in the environment. The CDM is calculated in closed form for several different function classes. An algorithm for training neural networks to implement the CDM is presented along with some encouraging experimental results.

Learning Model Bias

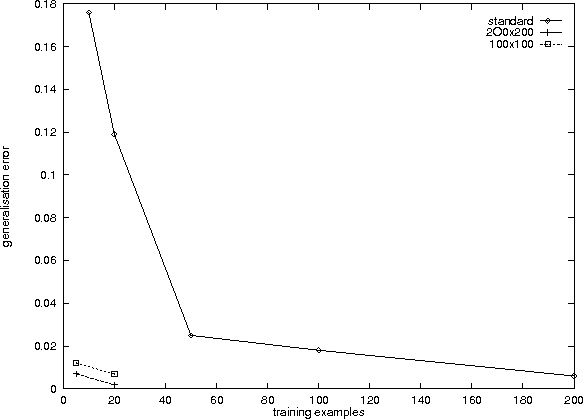
In this paper the problem of {\em learning} appropriate domain-specific bias is addressed. It is shown that this can be achieved by learning many related tasks from the same domain, and a theorem is given bounding the number tasks that must be learnt. A corollary of the theorem is that if the tasks are known to possess a common {\em internal representation} or {\em preprocessing} then the number of examples required per task for good generalisation when learning $n$ tasks simultaneously scales like $O(a + \frac{b}{n})$, where $O(a)$ is a bound on the minimum number of examples required to learn a single task, and $O(a + b)$ is a bound on the number of examples required to learn each task independently. An experiment providing strong qualitative support for the theoretical results is reported.

A Bayesian/Information Theoretic Model of Bias Learning

In this paper the problem of learning appropriate bias for an environment of related tasks is examined from a Bayesian perspective. The environment of related tasks is shown to be naturally modelled by the concept of an {\em objective} prior distribution. Sampling from the objective prior corresponds to sampling different learning tasks from the environment. It is argued that for many common machine learning problems, although we don't know the true (objective) prior for the problem, we do have some idea of a set of possible priors to which the true prior belongs. It is shown that under these circumstances a learner can use Bayesian inference to learn the true prior by sampling from the objective prior. Bounds are given on the amount of information required to learn a task when it is simultaneously learnt with several other tasks. The bounds show that if the learner has little knowledge of the true prior, and the dimensionality of the true prior is small, then sampling multiple tasks is highly advantageous.