Scaling up Stability: Reinforcement Learning for Distributed Control of Networked Systems in the Space of Stabilizing Policies

We study distributed control of networked systems through reinforcement learning, where neural policies must be simultaneously scalable, expressive and stabilizing. We introduce a policy parameterization that embeds Graph Neural Networks (GNNs) into a Youla-like magnitude-direction parameterization, yielding distributed stochastic controllers that guarantee network-level closed-loop stability by design. The magnitude is implemented as a stable operator consisting of a GNN acting on disturbance feedback, while the direction is a GNN acting on local observations. We prove robustness of the closed loop to perturbations in both the graph topology and model parameters, and show how to integrate our parameterization with Proximal Policy Optimization. Experiments on a multi-agent navigation task show that policies trained on small networks transfer directly to larger ones and unseen network topologies, achieve higher returns and lower variance than a state-of-the-art MARL baseline while preserving stability.

KKL Observer Synthesis for Nonlinear Systems via Physics-Informed Learning

This paper proposes a novel learning approach for designing Kazantzis-Kravaris/Luenberger (KKL) observers for autonomous nonlinear systems. The design of a KKL observer involves finding an injective map that transforms the system state into a higher-dimensional observer state, whose dynamics is linear and stable. The observer's state is then mapped back to the original system coordinates via the inverse map to obtain the state estimate. However, finding this transformation and its inverse is quite challenging. We propose to sequentially approximate these maps by neural networks that are trained using physics-informed learning. We generate synthetic data for training by numerically solving the system and observer dynamics. Theoretical guarantees for the robustness of state estimation against approximation error and system uncertainties are provided. Additionally, a systematic method for optimizing observer performance through parameter selection is presented. The effectiveness of the proposed approach is demonstrated through numerical simulations on benchmark examples and its application to sensor fault detection and isolation in a network of Kuramoto oscillators using learned KKL observers.

Sensor Fault Detection and Isolation in Autonomous Nonlinear Systems Using Neural Network-Based Observers

This paper presents a new observer-based approach to detect and isolate faulty sensors in industrial systems. Two types of sensor faults are considered: complete failure and sensor deterioration. The proposed method is applicable to general autonomous nonlinear systems without making any assumptions about its triangular and/or normal form, which is usually considered in the observer design literature. The key aspect of our approach is a learning-based design of the Luenberger observer, which involves using a neural network to approximate the injective map that transforms the nonlinear system into a stable linear system with output injection. This learning-based Luenberger observer accurately estimates the system's state, allowing for the detection of sensor faults through residual generation. The residual is computed as the norm of the difference between the system's measured output and the observer's predicted output vectors. Fault isolation is achieved by comparing each sensor's measurement with its corresponding predicted value. We demonstrate the effectiveness of our approach in capturing and isolating sensor faults while remaining robust in the presence of measurement noise and system uncertainty. We validate our method through numerical simulations of sensor faults in a network of Kuramoto oscillators.

Learning-based Design of Luenberger Observers for Autonomous Nonlinear Systems

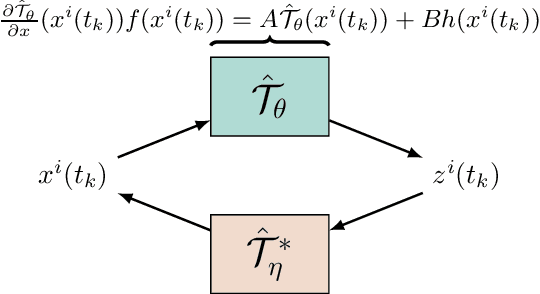
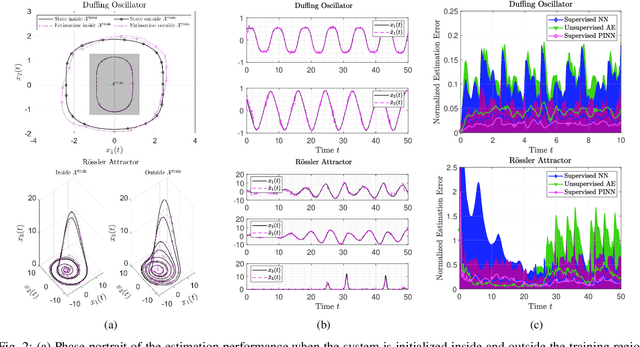
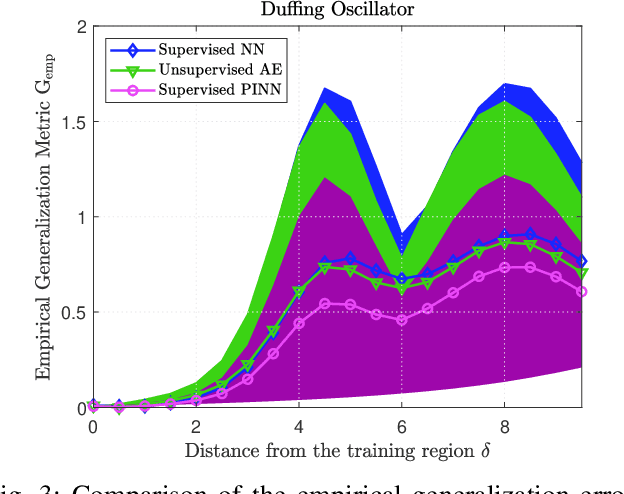
The design of Luenberger observers for nonlinear systems involves state transformation to another coordinate system where the dynamics are asymptotically stable and linear up to output injection. The observer then provides a state estimate in the original coordinates by inverting the transformation map. For general nonlinear systems, however, the main challenge is to find such a transformation and to ensure that it is injective. This paper addresses this challenge by proposing a learning method that employs supervised physics-informed neural networks to approximate both the transformation and its inverse. It is shown that the proposed method exhibits better generalization capabilities than other contemporary methods. Moreover, the observer is shown to be robust under the neural network's approximation error and the system uncertainties.