An Efficient Variant of One-Class SVM with Lifelong Online Learning Guarantees

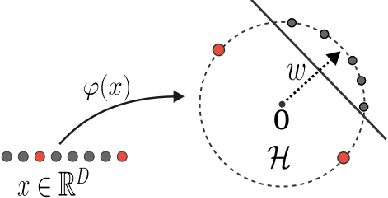
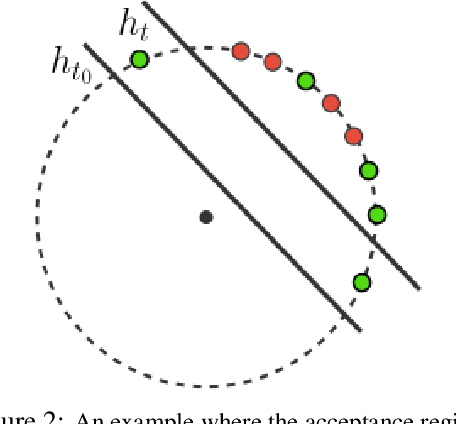
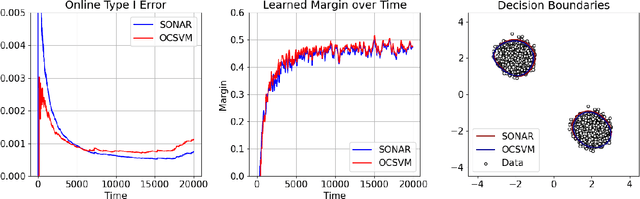
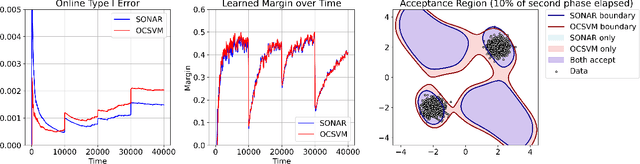
We study outlier (a.k.a., anomaly) detection for single-pass non-stationary streaming data. In the well-studied offline or batch outlier detection problem, traditional methods such as kernel One-Class SVM (OCSVM) are both computationally heavy and prone to large false-negative (Type II) errors under non-stationarity. To remedy this, we introduce SONAR, an efficient SGD-based OCSVM solver with strongly convex regularization. We show novel theoretical guarantees on the Type I/II errors of SONAR, superior to those known for OCSVM, and further prove that SONAR ensures favorable lifelong learning guarantees under benign distribution shifts. In the more challenging problem of adversarial non-stationary data, we show that SONAR can be used within an ensemble method and equipped with changepoint detection to achieve adaptive guarantees, ensuring small Type I/II errors on each phase of data. We validate our theoretical findings on synthetic and real-world datasets.

Adaptive Smooth Non-Stationary Bandits

We study a $K$-armed non-stationary bandit model where rewards change smoothly, as captured by H\"{o}lder class assumptions on rewards as functions of time. Such smooth changes are parametrized by a H\"{o}lder exponent $\beta$ and coefficient $\lambda$. While various sub-cases of this general model have been studied in isolation, we first establish the minimax dynamic regret rate generally for all $K,\beta,\lambda$. Next, we show this optimal dynamic regret can be attained adaptively, without knowledge of $\beta,\lambda$. To contrast, even with parameter knowledge, upper bounds were only previously known for limited regimes $\beta\leq 1$ and $\beta=2$ (Slivkins, 2014; Krishnamurthy and Gopalan, 2021; Manegueu et al., 2021; Jia et al.,2023). Thus, our work resolves open questions raised by these disparate threads of the literature. We also study the problem of attaining faster gap-dependent regret rates in non-stationary bandits. While such rates are long known to be impossible in general (Garivier and Moulines, 2011), we show that environments admitting a safe arm (Suk and Kpotufe, 2022) allow for much faster rates than the worst-case scaling with $\sqrt{T}$. While previous works in this direction focused on attaining the usual logarithmic regret bounds, as summed over stationary periods, our new gap-dependent rates reveal new optimistic regimes of non-stationarity where even the logarithmic bounds are pessimistic. We show our new gap-dependent rate is tight and that its achievability (i.e., as made possible by a safe arm) has a surprisingly simple and clean characterization within the smooth H\"{o}lder class model.

Optimal and Adaptive Non-Stationary Dueling Bandits Under a Generalized Borda Criterion

In dueling bandits, the learner receives preference feedback between arms, and the regret of an arm is defined in terms of its suboptimality to a winner arm. The more challenging and practically motivated non-stationary variant of dueling bandits, where preferences change over time, has been the focus of several recent works (Saha and Gupta, 2022; Buening and Saha, 2023; Suk and Agarwal, 2023). The goal is to design algorithms without foreknowledge of the amount of change. The bulk of known results here studies the Condorcet winner setting, where an arm preferred over any other exists at all times. Yet, such a winner may not exist and, to contrast, the Borda version of this problem (which is always well-defined) has received little attention. In this work, we establish the first optimal and adaptive Borda dynamic regret upper bound, which highlights fundamental differences in the learnability of severe non-stationarity between Condorcet vs. Borda regret objectives in dueling bandits. Surprisingly, our techniques for non-stationary Borda dueling bandits also yield improved rates within the Condorcet winner setting, and reveal new preference models where tighter notions of non-stationarity are adaptively learnable. This is accomplished through a novel generalized Borda score framework which unites the Borda and Condorcet problems, thus allowing reduction of Condorcet regret to a Borda-like task. Such a generalization was not previously known and is likely to be of independent interest.

Tracking Most Significant Shifts in Nonparametric Contextual Bandits

We study nonparametric contextual bandits where Lipschitz mean reward functions may change over time. We first establish the minimax dynamic regret rate in this less understood setting in terms of number of changes $L$ and total-variation $V$, both capturing all changes in distribution over context space, and argue that state-of-the-art procedures are suboptimal in this setting. Next, we tend to the question of an adaptivity for this setting, i.e. achieving the minimax rate without knowledge of $L$ or $V$. Quite importantly, we posit that the bandit problem, viewed locally at a given context $X_t$, should not be affected by reward changes in other parts of context space $\cal X$. We therefore propose a notion of change, which we term experienced significant shifts, that better accounts for locality, and thus counts considerably less changes than $L$ and $V$. Furthermore, similar to recent work on non-stationary MAB (Suk & Kpotufe, 2022), experienced significant shifts only count the most significant changes in mean rewards, e.g., severe best-arm changes relevant to observed contexts. Our main result is to show that this more tolerant notion of change can in fact be adapted to.

When Can We Track Significant Preference Shifts in Dueling Bandits?

The $K$-armed dueling bandits problem, where the feedback is in the form of noisy pairwise preferences, has been widely studied due its applications in information retrieval, recommendation systems, etc. Motivated by concerns that user preferences/tastes can evolve over time, we consider the problem of dueling bandits with distribution shifts. Specifically, we study the recent notion of significant shifts (Suk and Kpotufe, 2022), and ask whether one can design an adaptive algorithm for the dueling problem with $O(\sqrt{K\tilde{L}T})$ dynamic regret, where $\tilde{L}$ is the (unknown) number of significant shifts in preferences. We show that the answer to this question depends on the properties of underlying preference distributions. Firstly, we give an impossibility result that rules out any algorithm with $O(\sqrt{K\tilde{L}T})$ dynamic regret under the well-studied Condorcet and SST classes of preference distributions. Secondly, we show that $\text{SST} \cap \text{STI}$ is the largest amongst popular classes of preference distributions where it is possible to design such an algorithm. Overall, our results provides an almost complete resolution of the above question for the hierarchy of distribution classes.

Tracking Most Severe Arm Changes in Bandits

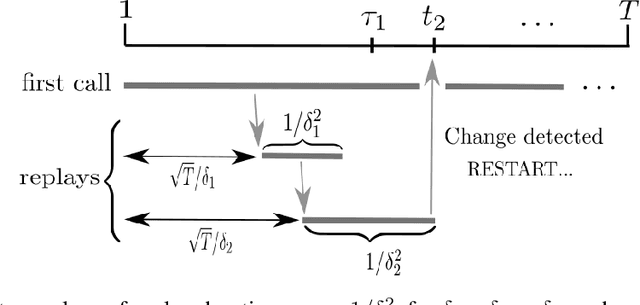
In bandits with distribution shifts, one aims to automatically detect an unknown number $L$ of changes in reward distribution, and restart exploration when necessary. While this problem remained open for many years, a recent breakthrough of Auer et al. (2018, 2019) provide the first adaptive procedure to guarantee an optimal (dynamic) regret $\sqrt{LT}$, for $T$ rounds, with no knowledge of $L$. However, not all distributional shifts are equally severe, e.g., suppose no best arm switches occur, then we cannot rule out that a regret $O(\sqrt{T})$ may remain possible; in other words, is it possible to achieve dynamic regret that optimally scales only with an unknown number of severe shifts? This unfortunately has remained elusive, despite various attempts (Auer et al., 2019, Foster et al., 2020). We resolve this problem in the case of two-armed bandits: we derive an adaptive procedure that guarantees a dynamic regret of order $\tilde{O}(\sqrt{\tilde{L} T})$, where $\tilde L \ll L$ captures an unknown number of severe best arm changes, i.e., with significant switches in rewards, and which last sufficiently long to actually require a restart. As a consequence, for any number $L$ of distributional shifts outside of these severe shifts, our procedure achieves regret just $\tilde{O}(\sqrt{T})\ll \tilde{O}(\sqrt{LT})$. Finally, we note that our notion of severe shift applies in both classical settings of stochastic switching bandits and of adversarial bandits.