Mitigating Forgetting in Low Rank Adaptation

Parameter-efficient fine-tuning methods, such as Low-Rank Adaptation (LoRA), enable fast specialization of large pre-trained models to different downstream applications. However, this process often leads to catastrophic forgetting of the model's prior domain knowledge. We address this issue with LaLoRA, a weight-space regularization technique that applies a Laplace approximation to Low-Rank Adaptation. Our approach estimates the model's confidence in each parameter and constrains updates in high-curvature directions, preserving prior knowledge while enabling efficient target-domain learning. By applying the Laplace approximation only to the LoRA weights, the method remains lightweight. We evaluate LaLoRA by fine-tuning a Llama model for mathematical reasoning and demonstrate an improved learning-forgetting trade-off, which can be directly controlled via the method's regularization strength. We further explore different loss landscape curvature approximations for estimating parameter confidence, analyze the effect of the data used for the Laplace approximation, and study robustness across hyperparameters.

Efficient Weight-Space Laplace-Gaussian Filtering and Smoothing for Sequential Deep Learning

Efficiently learning a sequence of related tasks, such as in continual learning, poses a significant challenge for neural nets due to the delicate trade-off between catastrophic forgetting and loss of plasticity. We address this challenge with a grounded framework for sequentially learning related tasks based on Bayesian inference. Specifically, we treat the model's parameters as a nonlinear Gaussian state-space model and perform efficient inference using Gaussian filtering and smoothing. This general formalism subsumes existing continual learning approaches, while also offering a clearer conceptual understanding of its components. Leveraging Laplace approximations during filtering, we construct Gaussian posterior measures on the weight space of a neural network for each task. We use it as an efficient regularizer by exploiting the structure of the generalized Gauss-Newton matrix (GGN) to construct diagonal plus low-rank approximations. The dynamics model allows targeted control of the learning process and the incorporation of domain-specific knowledge, such as modeling the type of shift between tasks. Additionally, using Bayesian approximate smoothing can enhance the performance of task-specific models without needing to re-access any data.

Probing the Robustness of Independent Mechanism Analysis for Representation Learning

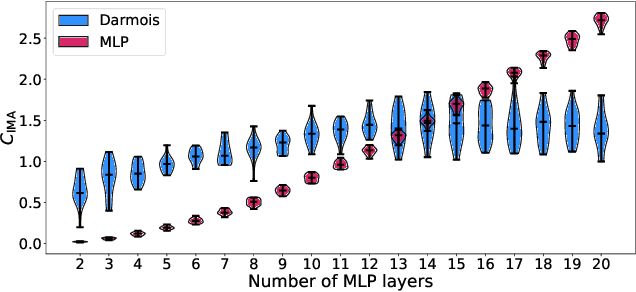
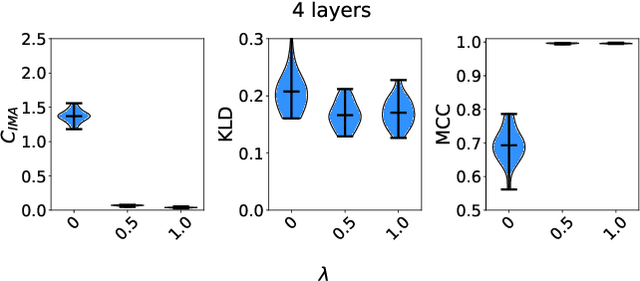
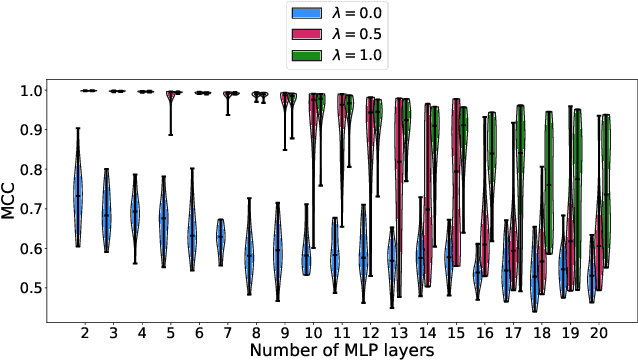
One aim of representation learning is to recover the original latent code that generated the data, a task which requires additional information or inductive biases. A recently proposed approach termed Independent Mechanism Analysis (IMA) postulates that each latent source should influence the observed mixtures independently, complementing standard nonlinear independent component analysis, and taking inspiration from the principle of independent causal mechanisms. While it was shown in theory and experiments that IMA helps recovering the true latents, the method's performance was so far only characterized when the modeling assumptions are exactly satisfied. Here, we test the method's robustness to violations of the underlying assumptions. We find that the benefits of IMA-based regularization for recovering the true sources extend to mixing functions with various degrees of violation of the IMA principle, while standard regularizers do not provide the same merits. Moreover, we show that unregularized maximum likelihood recovers mixing functions which systematically deviate from the IMA principle, and provide an argument elucidating the benefits of IMA-based regularization.