Beyond backpropagation: implicit gradients for bilevel optimization

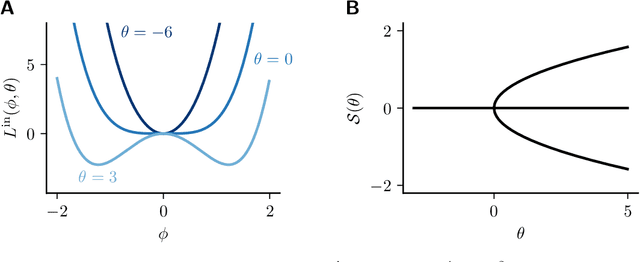
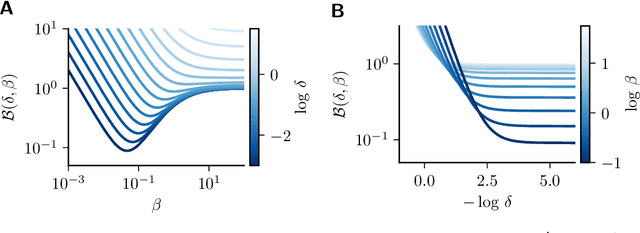
This paper reviews gradient-based techniques to solve bilevel optimization problems. Bilevel optimization is a general way to frame the learning of systems that are implicitly defined through a quantity that they minimize. This characterization can be applied to neural networks, optimizers, algorithmic solvers and even physical systems, and allows for greater modeling flexibility compared to an explicit definition of such systems. Here we focus on gradient-based approaches that solve such problems. We distinguish them in two categories: those rooted in implicit differentiation, and those that leverage the equilibrium propagation theorem. We present the mathematical foundations that are behind such methods, introduce the gradient-estimation algorithms in detail and compare the competitive advantages of the different approaches.

Minimizing Control for Credit Assignment with Strong Feedback

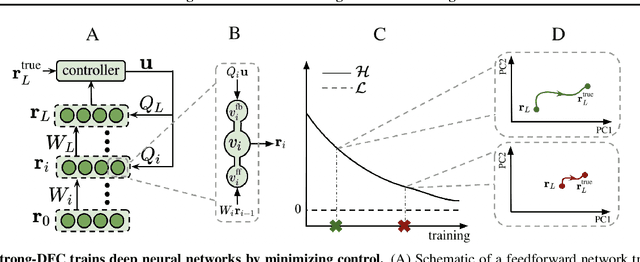
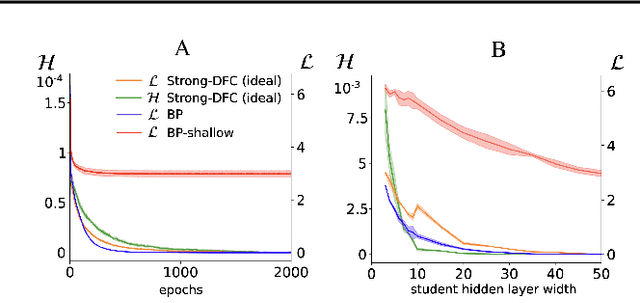
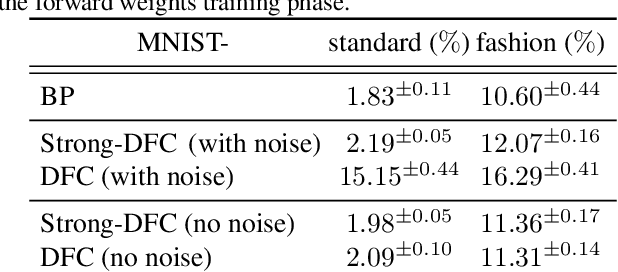
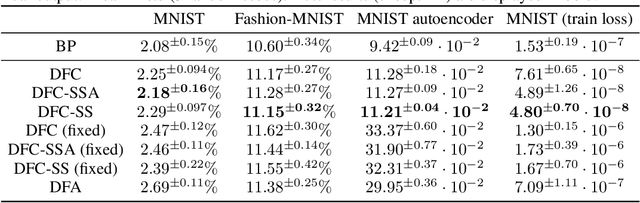
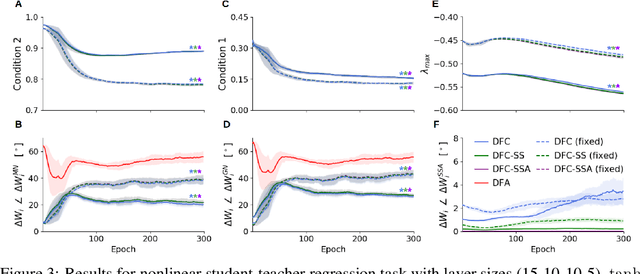
The success of deep learning attracted interest in whether the brain learns hierarchical representations using gradient-based learning. However, current biologically plausible methods for gradient-based credit assignment in deep neural networks need infinitesimally small feedback signals, which is problematic in biologically realistic noisy environments and at odds with experimental evidence in neuroscience showing that top-down feedback can significantly influence neural activity. Building upon deep feedback control (DFC), a recently proposed credit assignment method, we combine strong feedback influences on neural activity with gradient-based learning and show that this naturally leads to a novel view on neural network optimization. Instead of gradually changing the network weights towards configurations with low output loss, weight updates gradually minimize the amount of feedback required from a controller that drives the network to the supervised output label. Moreover, we show that the use of strong feedback in DFC allows learning forward and feedback connections simultaneously, using a learning rule fully local in space and time. We complement our theoretical results with experiments on standard computer-vision benchmarks, showing competitive performance to backpropagation as well as robustness to noise. Overall, our work presents a fundamentally novel view of learning as control minimization, while sidestepping biologically unrealistic assumptions.

Learning where to learn: Gradient sparsity in meta and continual learning

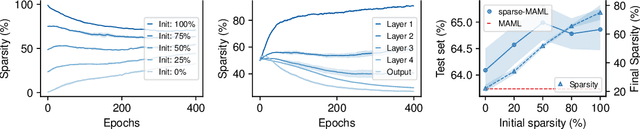
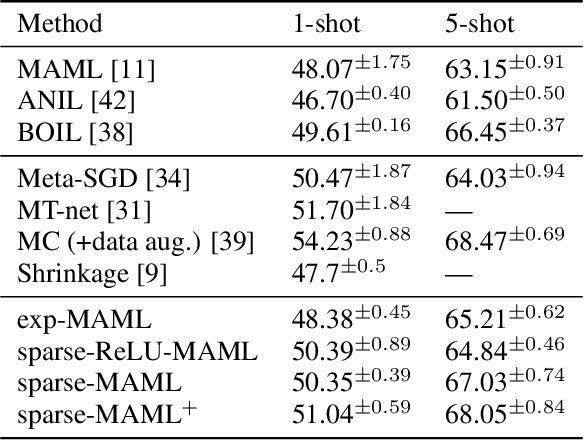
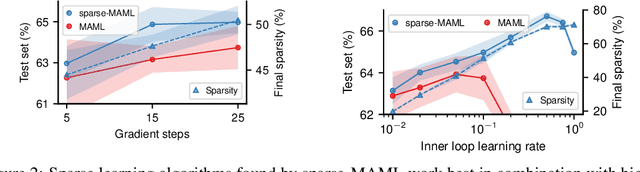
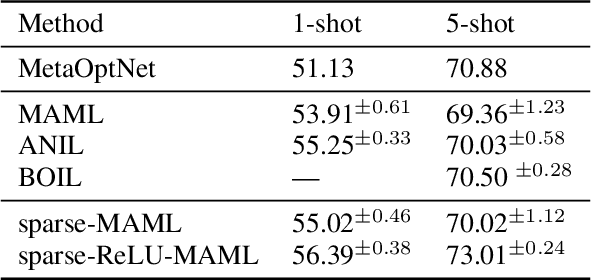
Finding neural network weights that generalize well from small datasets is difficult. A promising approach is to learn a weight initialization such that a small number of weight changes results in low generalization error. We show that this form of meta-learning can be improved by letting the learning algorithm decide which weights to change, i.e., by learning where to learn. We find that patterned sparsity emerges from this process, with the pattern of sparsity varying on a problem-by-problem basis. This selective sparsity results in better generalization and less interference in a range of few-shot and continual learning problems. Moreover, we find that sparse learning also emerges in a more expressive model where learning rates are meta-learned. Our results shed light on an ongoing debate on whether meta-learning can discover adaptable features and suggest that learning by sparse gradient descent is a powerful inductive bias for meta-learning systems.

Credit Assignment in Neural Networks through Deep Feedback Control

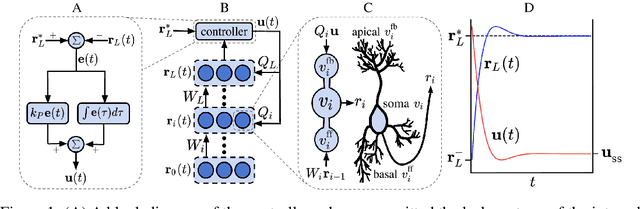
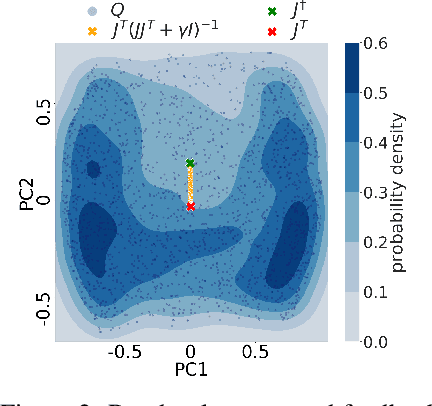
The success of deep learning sparked interest in whether the brain learns by using similar techniques for assigning credit to each synaptic weight for its contribution to the network output. However, the majority of current attempts at biologically-plausible learning methods are either non-local in time, require highly specific connectivity motives, or have no clear link to any known mathematical optimization method. Here, we introduce Deep Feedback Control (DFC), a new learning method that uses a feedback controller to drive a deep neural network to match a desired output target and whose control signal can be used for credit assignment. The resulting learning rule is fully local in space and time and approximates Gauss-Newton optimization for a wide range of feedback connectivity patterns. To further underline its biological plausibility, we relate DFC to a multi-compartment model of cortical pyramidal neurons with a local voltage-dependent synaptic plasticity rule, consistent with recent theories of dendritic processing. By combining dynamical system theory with mathematical optimization theory, we provide a strong theoretical foundation for DFC that we corroborate with detailed results on toy experiments and standard computer-vision benchmarks.

A contrastive rule for meta-learning

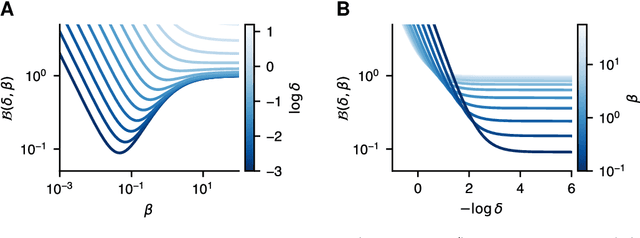
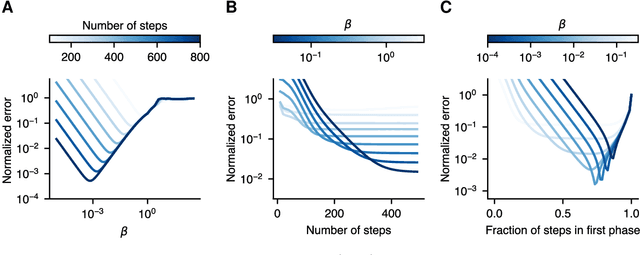
Meta-learning algorithms leverage regularities that are present on a set of tasks to speed up and improve the performance of a subsidiary learning process. Recent work on deep neural networks has shown that prior gradient-based learning of meta-parameters can greatly improve the efficiency of subsequent learning. Here, we present a biologically plausible meta-learning algorithm based on equilibrium propagation. Instead of explicitly differentiating the learning process, our contrastive meta-learning rule estimates meta-parameter gradients by executing the subsidiary process more than once. This avoids reversing the learning dynamics in time and computing second-order derivatives. In spite of this, and unlike previous first-order methods, our rule recovers an arbitrarily accurate meta-parameter update given enough compute. We establish theoretical bounds on its performance and present experiments on a set of standard benchmarks and neural network architectures.

Posterior Meta-Replay for Continual Learning

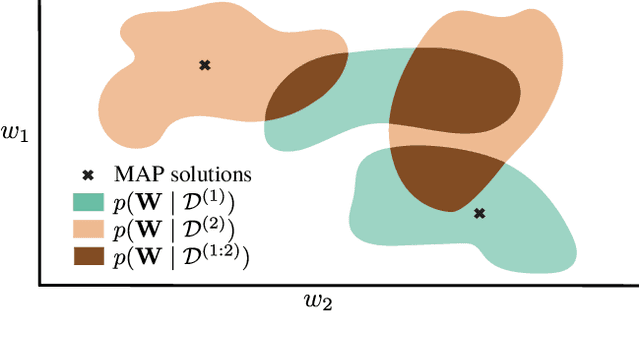
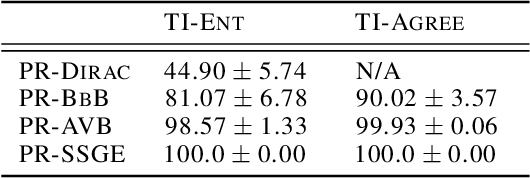
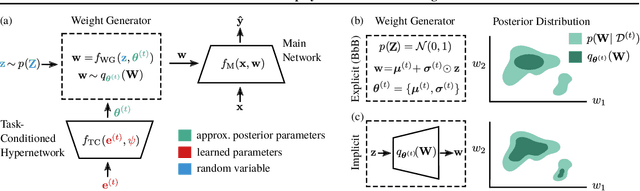
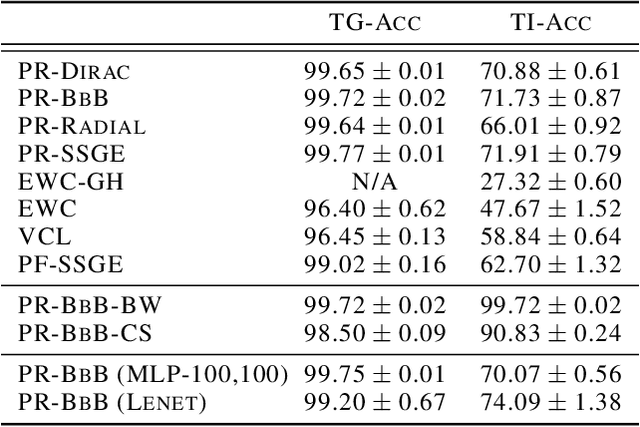
Continual Learning (CL) algorithms have recently received a lot of attention as they attempt to overcome the need to train with an i.i.d. sample from some unknown target data distribution. Building on prior work, we study principled ways to tackle the CL problem by adopting a Bayesian perspective and focus on continually learning a task-specific posterior distribution via a shared meta-model, a task-conditioned hypernetwork. This approach, which we term Posterior-replay CL, is in sharp contrast to most Bayesian CL approaches that focus on the recursive update of a single posterior distribution. The benefits of our approach are (1) an increased flexibility to model solutions in weight space and therewith less susceptibility to task dissimilarity, (2) access to principled task-specific predictive uncertainty estimates, that can be used to infer task identity during test time and to detect task boundaries during training, and (3) the ability to revisit and update task-specific posteriors in a principled manner without requiring access to past data. The proposed framework is versatile, which we demonstrate using simple posterior approximations (such as Gaussians) as well as powerful, implicit distributions modelled via a neural network. We illustrate the conceptual advance of our framework on low-dimensional problems and show performance gains on computer vision benchmarks.

Economical ensembles with hypernetworks

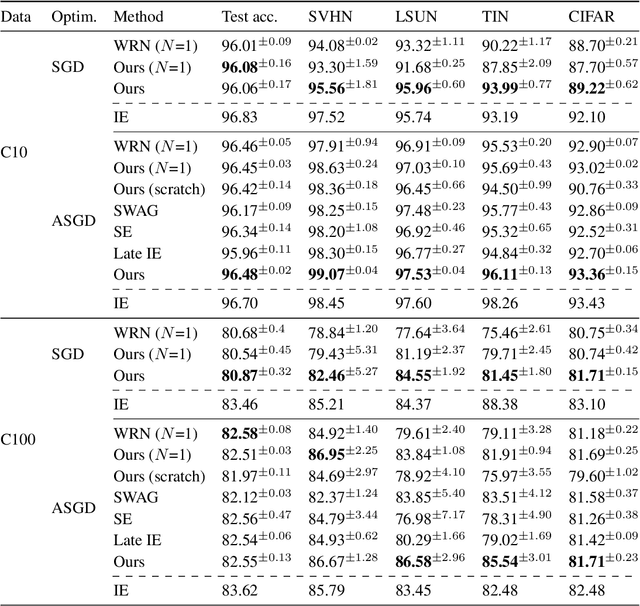
Averaging the predictions of many independently trained neural networks is a simple and effective way of improving generalization in deep learning. However, this strategy rapidly becomes costly, as the number of trainable parameters grows linearly with the size of the ensemble. Here, we propose a new method to learn economical ensembles, where the number of trainable parameters and iterations over the data is comparable to that of a single model. Our neural networks are parameterized by hypernetworks, which learn to embed weights in low-dimensional spaces. In a late training phase, we generate an ensemble by randomly initializing an additional number of weight embeddings in the vicinity of each other. We then exploit the inherent randomness in stochastic gradient descent to induce ensemble diversity. Experiments with wide residual networks on the CIFAR and Fashion-MNIST datasets show that our algorithm yields models that are more accurate and less overconfident on unseen data, while learning as efficiently as a single network.

A Theoretical Framework for Target Propagation

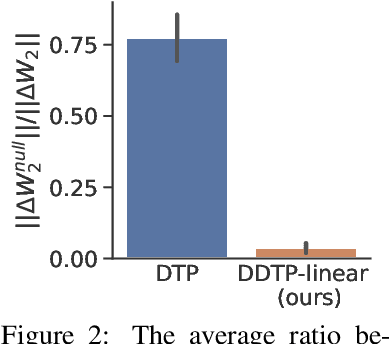
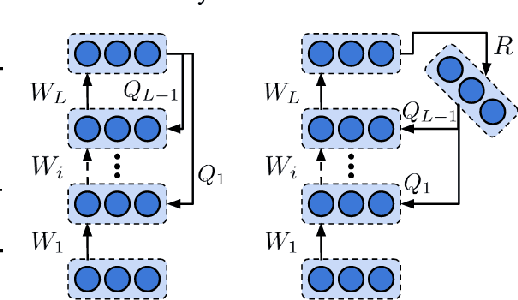
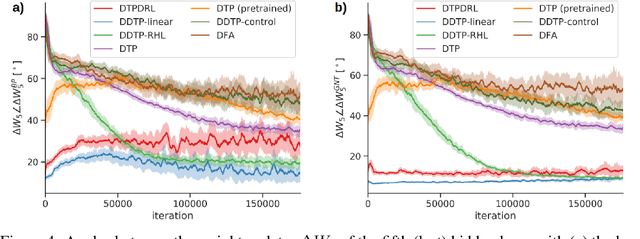
The success of deep learning, a brain-inspired form of AI, has sparked interest in understanding how the brain could similarly learn across multiple layers of neurons. However, the majority of biologically-plausible learning algorithms have not yet reached the performance of backpropagation (BP), nor are they built on strong theoretical foundations. Here, we analyze target propagation (TP), a popular but not yet fully understood alternative to BP, from the standpoint of mathematical optimization. Our theory shows that TP is closely related to Gauss-Newton optimization and thus substantially differs from BP. Furthermore, our analysis reveals a fundamental limitation of difference target propagation (DTP), a well-known variant of TP, in the realistic scenario of non-invertible neural networks. We provide a first solution to this problem through a novel reconstruction loss that improves feedback weight training, while simultaneously introducing architectural flexibility by allowing for direct feedback connections from the output to each hidden layer. Our theory is corroborated by experimental results that show significant improvements in performance and in the alignment of forward weight updates with loss gradients, compared to DTP.

Continual learning with hypernetworks

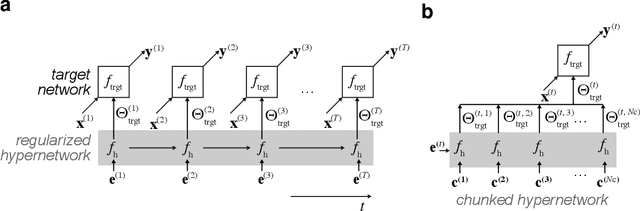
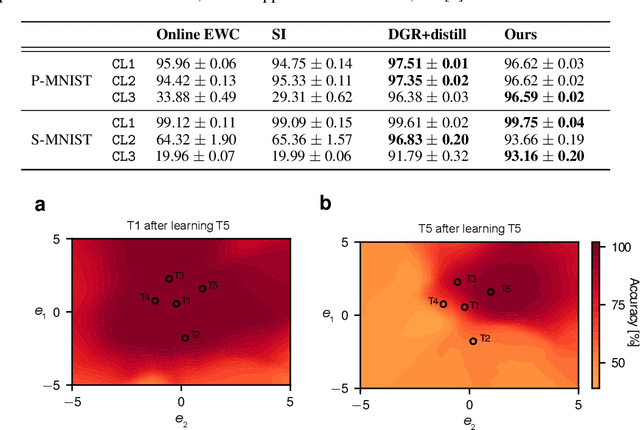
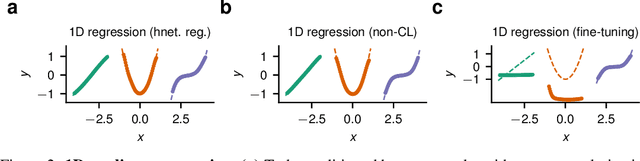
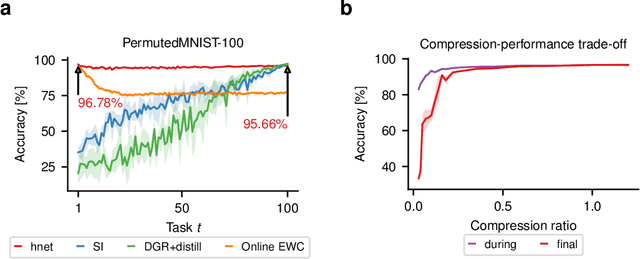
Artificial neural networks suffer from catastrophic forgetting when they are sequentially trained on multiple tasks. To overcome this problem, we present a novel approach based on task-conditioned hypernetworks, i.e., networks that generate the weights of a target model based on task identity. Continual learning (CL) is less difficult for this class of models thanks to a simple key observation: instead of relying on recalling the input-output relations of all previously seen data, task-conditioned hypernetworks only require rehearsing previous weight realizations, which can be maintained in memory using a simple regularizer. Besides achieving good performance on standard CL benchmarks, additional experiments on long task sequences reveal that task-conditioned hypernetworks display an unprecedented capacity to retain previous memories. Notably, such long memory lifetimes are achieved in a compressive regime, when the number of trainable weights is comparable or smaller than target network size. We provide insight into the structure of low-dimensional task embedding spaces (the input space of the hypernetwork) and show that task-conditioned hypernetworks demonstrate transfer learning properties. Finally, forward information transfer is further supported by empirical results on a challenging CL benchmark based on the CIFAR-10/100 image datasets.

Dendritic cortical microcircuits approximate the backpropagation algorithm

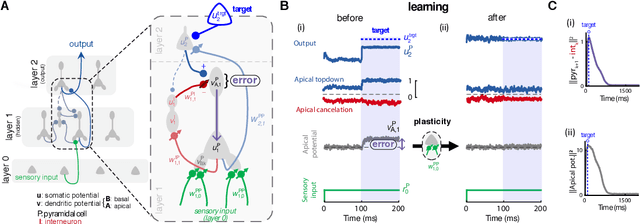
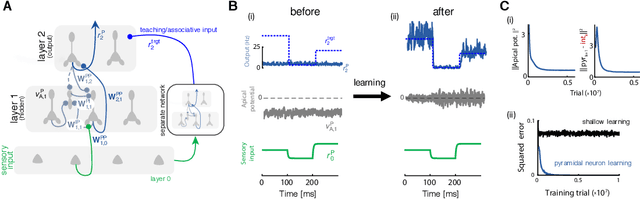
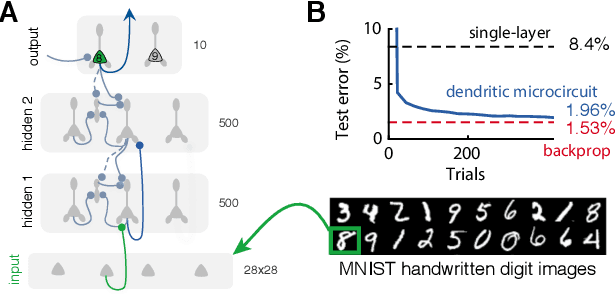
Deep learning has seen remarkable developments over the last years, many of them inspired by neuroscience. However, the main learning mechanism behind these advances - error backpropagation - appears to be at odds with neurobiology. Here, we introduce a multilayer neuronal network model with simplified dendritic compartments in which error-driven synaptic plasticity adapts the network towards a global desired output. In contrast to previous work our model does not require separate phases and synaptic learning is driven by local dendritic prediction errors continuously in time. Such errors originate at apical dendrites and occur due to a mismatch between predictive input from lateral interneurons and activity from actual top-down feedback. Through the use of simple dendritic compartments and different cell-types our model can represent both error and normal activity within a pyramidal neuron. We demonstrate the learning capabilities of the model in regression and classification tasks, and show analytically that it approximates the error backpropagation algorithm. Moreover, our framework is consistent with recent observations of learning between brain areas and the architecture of cortical microcircuits. Overall, we introduce a novel view of learning on dendritic cortical circuits and on how the brain may solve the long-standing synaptic credit assignment problem.