Indexed Minimum Empirical Divergence-Based Algorithms for Linear Bandits

The Indexed Minimum Empirical Divergence (IMED) algorithm is a highly effective approach that offers a stronger theoretical guarantee of the asymptotic optimality compared to the Kullback--Leibler Upper Confidence Bound (KL-UCB) algorithm for the multi-armed bandit problem. Additionally, it has been observed to empirically outperform UCB-based algorithms and Thompson Sampling. Despite its effectiveness, the generalization of this algorithm to contextual bandits with linear payoffs has remained elusive. In this paper, we present novel linear versions of the IMED algorithm, which we call the family of LinIMED algorithms. We demonstrate that LinIMED provides a $\widetilde{O}(d\sqrt{T})$ upper regret bound where $d$ is the dimension of the context and $T$ is the time horizon. Furthermore, extensive empirical studies reveal that LinIMED and its variants outperform widely-used linear bandit algorithms such as LinUCB and Linear Thompson Sampling in some regimes.

Maillard Sampling: Boltzmann Exploration Done Optimally

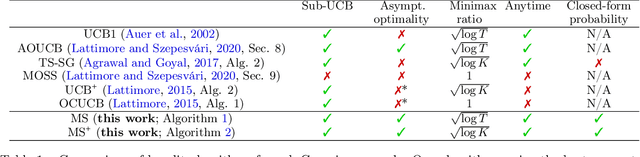
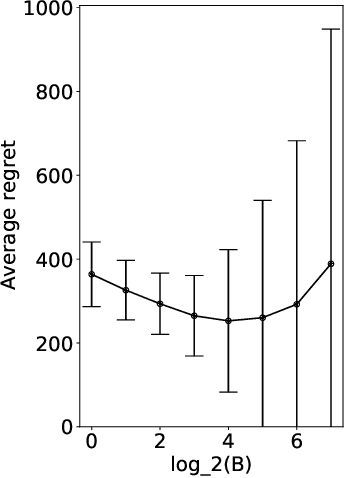
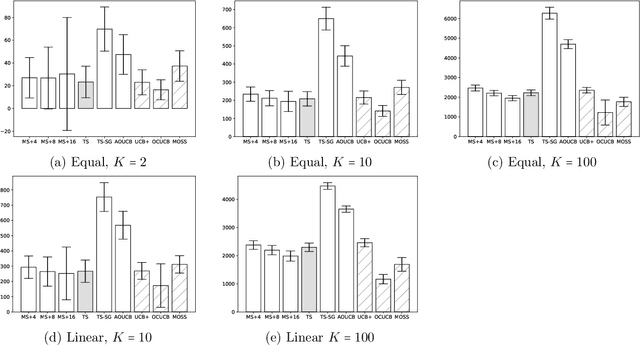
The PhD thesis of Maillard (2013) presents a randomized algorithm for the $K$-armed bandit problem. This less-known algorithm, which we call Maillard sampling (MS), computes the probability of choosing each arm in a closed form, which is useful for counterfactual evaluation from bandit-logged data but was lacking from Thompson sampling, a widely-adopted bandit algorithm in the industry. Motivated by such merit, we revisit MS and perform an improved analysis to show that it achieves both the asymptotical optimality and $\sqrt{KT\log{T}}$ minimax regret bound where $T$ is the time horizon, which matches the standard asymptotically optimal UCB's performance. We then propose a variant of MS called MS$^+$ that improves its minimax bound to $\sqrt{KT\log{K}}$ without losing the asymptotic optimality. MS$^+$ can also be tuned to be aggressive (i.e., less exploration) without losing theoretical guarantees, a unique feature unavailable from existing bandit algorithms. Our numerical evaluation shows the effectiveness of MS$^+$.