Optimal differentially private kernel learning with random projection

Differential privacy has become a cornerstone in the development of privacy-preserving learning algorithms. This work addresses optimizing differentially private kernel learning within the empirical risk minimization (ERM) framework. We propose a novel differentially private kernel ERM algorithm based on random projection in the reproducing kernel Hilbert space using Gaussian processes. Our method achieves minimax-optimal excess risk for both the squared loss and Lipschitz-smooth convex loss functions under a local strong convexity condition. We further show that existing approaches based on alternative dimension reduction techniques, such as random Fourier feature mappings or $\ell_2$ regularization, yield suboptimal generalization performance. Our key theoretical contribution also includes the derivation of dimension-free generalization bounds for objective perturbation-based private linear ERM -- marking the first such result that does not rely on noisy gradient-based mechanisms. Additionally, we obtain sharper generalization bounds for existing differentially private kernel ERM algorithms. Empirical evaluations support our theoretical claims, demonstrating that random projection enables statistically efficient and optimally private kernel learning. These findings provide new insights into the design of differentially private algorithms and highlight the central role of dimension reduction in balancing privacy and utility.

Reproducing Kernels and New Approaches in Compositional Data Analysis

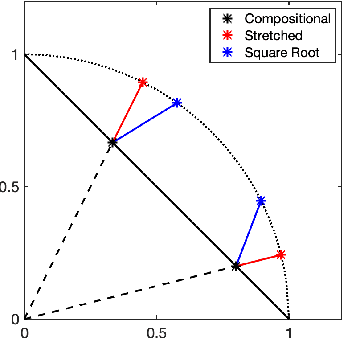
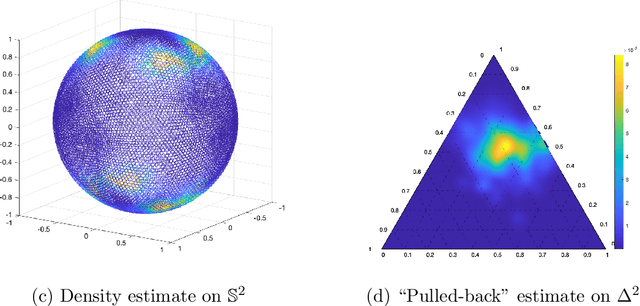
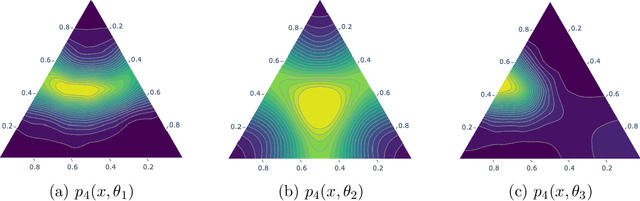
Compositional data, such as human gut microbiomes, consist of non-negative variables whose only the relative values to other variables are available. Analyzing compositional data such as human gut microbiomes needs a careful treatment of the geometry of the data. A common geometrical understanding of compositional data is via a regular simplex. Majority of existing approaches rely on a log-ratio or power transformations to overcome the innate simplicial geometry. In this work, based on the key observation that a compositional data are projective in nature, and on the intrinsic connection between projective and spherical geometry, we re-interpret the compositional domain as the quotient topology of a sphere modded out by a group action. This re-interpretation allows us to understand the function space on compositional domains in terms of that on spheres and to use spherical harmonics theory along with reflection group actions for constructing a compositional Reproducing Kernel Hilbert Space (RKHS). This construction of RKHS for compositional data will widely open research avenues for future methodology developments. In particular, well-developed kernel embedding methods can be now introduced to compositional data analysis. The polynomial nature of compositional RKHS has both theoretical and computational benefits. The wide applicability of the proposed theoretical framework is exemplified with nonparametric density estimation and kernel exponential family for compositional data.