Towards Kriging-informed Conditional Diffusion for Regional Sea-Level Data Downscaling

Given coarser-resolution projections from global climate models or satellite data, the downscaling problem aims to estimate finer-resolution regional climate data, capturing fine-scale spatial patterns and variability. Downscaling is any method to derive high-resolution data from low-resolution variables, often to provide more detailed and local predictions and analyses. This problem is societally crucial for effective adaptation, mitigation, and resilience against significant risks from climate change. The challenge arises from spatial heterogeneity and the need to recover finer-scale features while ensuring model generalization. Most downscaling methods \cite{Li2020} fail to capture the spatial dependencies at finer scales and underperform on real-world climate datasets, such as sea-level rise. We propose a novel Kriging-informed Conditional Diffusion Probabilistic Model (Ki-CDPM) to capture spatial variability while preserving fine-scale features. Experimental results on climate data show that our proposed method is more accurate than state-of-the-art downscaling techniques.

Reducing False Discoveries in Statistically-Significant Regional-Colocation Mining: A Summary of Results

Given a set \emph{S} of spatial feature types, its feature instances, a study area, and a neighbor relationship, the goal is to find pairs $<$a region ($r_{g}$), a subset \emph{C} of \emph{S}$>$ such that \emph{C} is a statistically significant regional-colocation pattern in $r_{g}$. This problem is important for applications in various domains including ecology, economics, and sociology. The problem is computationally challenging due to the exponential number of regional colocation patterns and candidate regions. Previously, we proposed a miner \cite{10.1145/3557989.3566158} that finds statistically significant regional colocation patterns. However, the numerous simultaneous statistical inferences raise the risk of false discoveries (also known as the multiple comparisons problem) and carry a high computational cost. We propose a novel algorithm, namely, multiple comparisons regional colocation miner (MultComp-RCM) which uses a Bonferroni correction. Theoretical analysis, experimental evaluation, and case study results show that the proposed method reduces both the false discovery rate and computational cost.

Towards Statistically Significant Taxonomy Aware Co-location Pattern Detection

Given a collection of Boolean spatial feature types, their instances, a neighborhood relation (e.g., proximity), and a hierarchical taxonomy of the feature types, the goal is to find the subsets of feature types or their parents whose spatial interaction is statistically significant. This problem is for taxonomy-reliant applications such as ecology (e.g., finding new symbiotic relationships across the food chain), spatial pathology (e.g., immunotherapy for cancer), retail, etc. The problem is computationally challenging due to the exponential number of candidate co-location patterns generated by the taxonomy. Most approaches for co-location pattern detection overlook the hierarchical relationships among spatial features, and the statistical significance of the detected patterns is not always considered, leading to potential false discoveries. This paper introduces two methods for incorporating taxonomies and assessing the statistical significance of co-location patterns. The baseline approach iteratively checks the significance of co-locations between leaf nodes or their ancestors in the taxonomy. Using the Benjamini-Hochberg procedure, an advanced approach is proposed to control the false discovery rate. This approach effectively reduces the risk of false discoveries while maintaining the power to detect true co-location patterns. Experimental evaluation and case study results show the effectiveness of the approach.

Towards Spatially-Lucid AI Classification in Non-Euclidean Space: An Application for MxIF Oncology Data

Given multi-category point sets from different place-types, our goal is to develop a spatially-lucid classifier that can distinguish between two classes based on the arrangements of their points. This problem is important for many applications, such as oncology, for analyzing immune-tumor relationships and designing new immunotherapies. It is challenging due to spatial variability and interpretability needs. Previously proposed techniques require dense training data or have limited ability to handle significant spatial variability within a single place-type. Most importantly, these deep neural network (DNN) approaches are not designed to work in non-Euclidean space, particularly point sets. Existing non-Euclidean DNN methods are limited to one-size-fits-all approaches. We explore a spatial ensemble framework that explicitly uses different training strategies, including weighted-distance learning rate and spatial domain adaptation, on various place-types for spatially-lucid classification. Experimental results on real-world datasets (e.g., MxIF oncology data) show that the proposed framework provides higher prediction accuracy than baseline methods.

Reducing Uncertainty in Sea-level Rise Prediction: A Spatial-variability-aware Approach

Given multi-model ensemble climate projections, the goal is to accurately and reliably predict future sea-level rise while lowering the uncertainty. This problem is important because sea-level rise affects millions of people in coastal communities and beyond due to climate change's impacts on polar ice sheets and the ocean. This problem is challenging due to spatial variability and unknowns such as possible tipping points (e.g., collapse of Greenland or West Antarctic ice-shelf), climate feedback loops (e.g., clouds, permafrost thawing), future policy decisions, and human actions. Most existing climate modeling approaches use the same set of weights globally, during either regression or deep learning to combine different climate projections. Such approaches are inadequate when different regions require different weighting schemes for accurate and reliable sea-level rise predictions. This paper proposes a zonal regression model which addresses spatial variability and model inter-dependency. Experimental results show more reliable predictions using the weights learned via this approach on a regional scale.

A Survey on Solving and Discovering Differential Equations Using Deep Neural Networks

Ordinary and partial differential equations (DE) are used extensively in scientific and mathematical domains to model physical systems. Current literature has focused primarily on deep neural network (DNN) based methods for solving a specific DE or a family of DEs. Research communities with a history of using DE models may view DNN-based differential equation solvers (DNN-DEs) as a faster and transferable alternative to current numerical methods. However, there is a lack of systematic surveys detailing the use of DNN-DE methods across physical application domains and a generalized taxonomy to guide future research. This paper surveys and classifies previous works and provides an educational tutorial for senior practitioners, professionals, and graduate students in engineering and computer science. First, we propose a taxonomy to navigate domains of DE systems studied under the umbrella of DNN-DE. Second, we examine the theory and performance of the Physics Informed Neural Network (PINN) to demonstrate how the influential DNN-DE architecture mathematically solves a system of equations. Third, to reinforce the key ideas of solving and discovery of DEs using DNN, we provide a tutorial using DeepXDE, a Python package for developing PINNs, to develop DNN-DEs for solving and discovering a classic DE, the linear transport equation.

Towards Comparative Physical Interpretation of Spatial Variability Aware Neural Networks: A Summary of Results

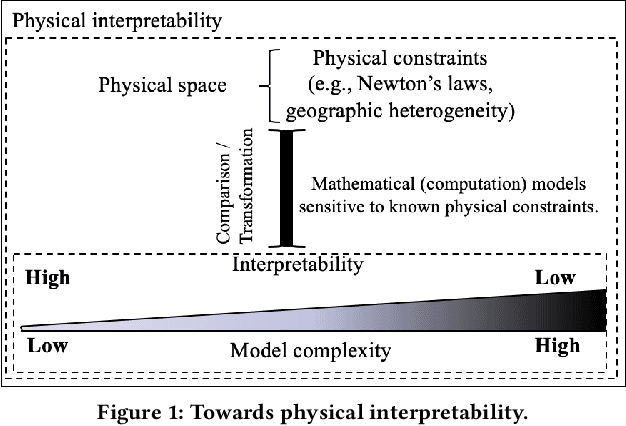
Given Spatial Variability Aware Neural Networks (SVANNs), the goal is to investigate mathematical (or computational) models for comparative physical interpretation towards their transparency (e.g., simulatibility, decomposability and algorithmic transparency). This problem is important due to important use-cases such as reusability, debugging, and explainability to a jury in a court of law. Challenges include a large number of model parameters, vacuous bounds on generalization performance of neural networks, risk of overfitting, sensitivity to noise, etc., which all detract from the ability to interpret the models. Related work on either model-specific or model-agnostic post-hoc interpretation is limited due to a lack of consideration of physical constraints (e.g., mass balance) and properties (e.g., second law of geography). This work investigates physical interpretation of SVANNs using novel comparative approaches based on geographically heterogeneous features. The proposed approach on feature-based physical interpretation is evaluated using a case-study on wetland mapping. The proposed physical interpretation improves the transparency of SVANN models and the analytical results highlight the trade-off between model transparency and model performance (e.g., F1-score). We also describe an interpretation based on geographically heterogeneous processes modeled as partial differential equations (PDEs).

Towards Spatial Variability Aware Deep Neural Networks (SVANN): A Summary of Results

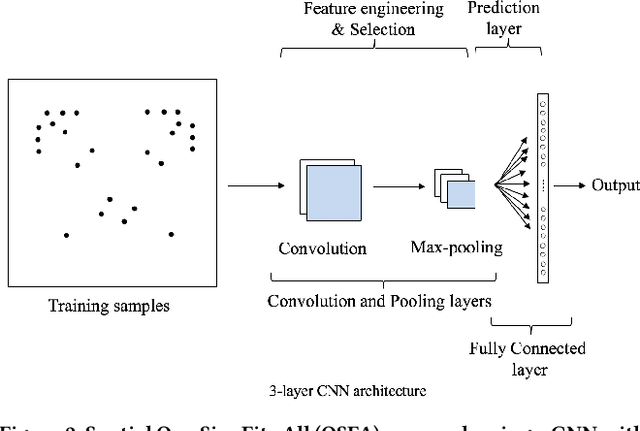
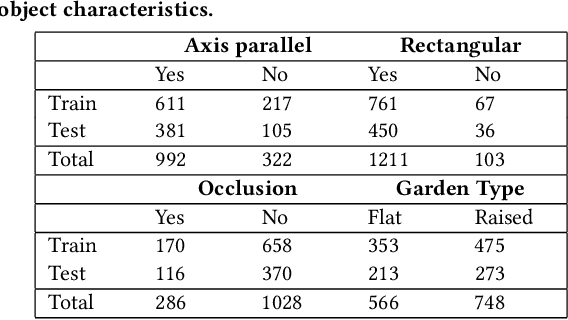
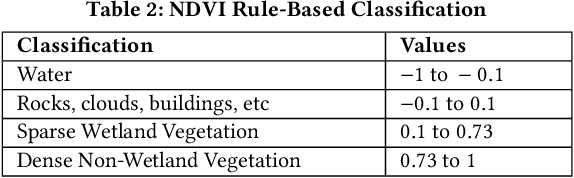
Spatial variability has been observed in many geo-phenomena including climatic zones, USDA plant hardiness zones, and terrestrial habitat types (e.g., forest, grasslands, wetlands, and deserts). However, current deep learning methods follow a spatial-one-size-fits-all(OSFA) approach to train single deep neural network models that do not account for spatial variability. In this work, we propose and investigate a spatial-variability aware deep neural network(SVANN) approach, where distinct deep neural network models are built for each geographic area. We evaluate this approach using aerial imagery from two geographic areas for the task of mapping urban gardens. The experimental results show that SVANN provides better performance than OSFA in terms of precision, recall,and F1-score to identify urban gardens.