Poisson multi-Bernoulli mixture filter: direct derivation and implementation

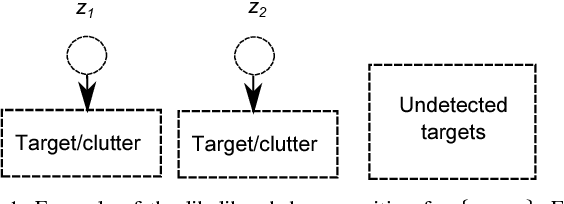
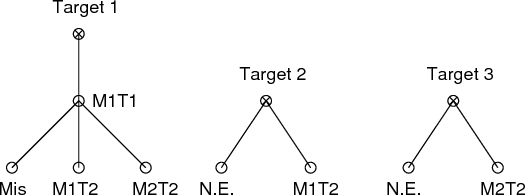
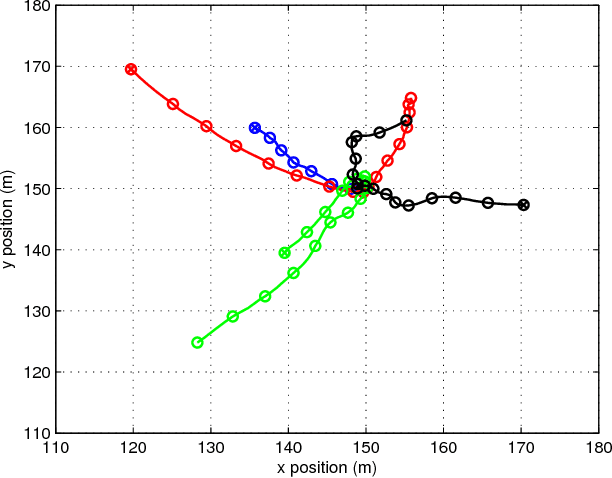
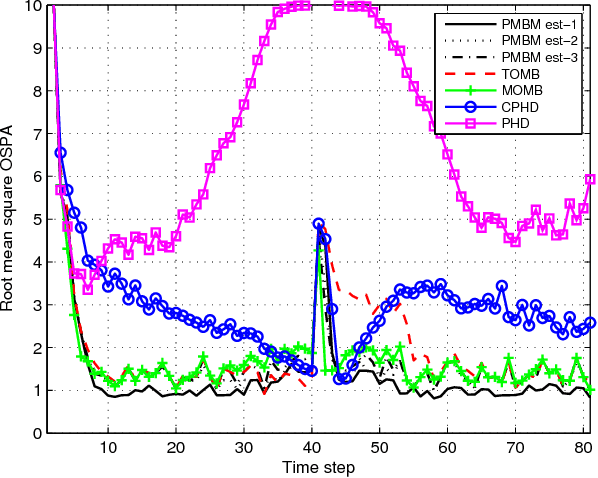
We provide a derivation of the Poisson multi-Bernoulli mixture (PMBM) filter for multi-target tracking with the standard point target measurements without using probability generating functionals or functional derivatives. We also establish the connection with the \delta-generalised labelled multi-Bernoulli (\delta-GLMB) filter, showing that a \delta-GLMB density represents a multi-Bernoulli mixture with labelled targets so it can be seen as a special case of PMBM. In addition, we propose an implementation for linear/Gaussian dynamic and measurement models and how to efficiently obtain typical estimators in the literature from the PMBM. The PMBM filter is shown to outperform other filters in the literature in a challenging scenario.

Multiple scan data association by convex variational inference

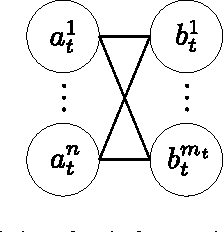
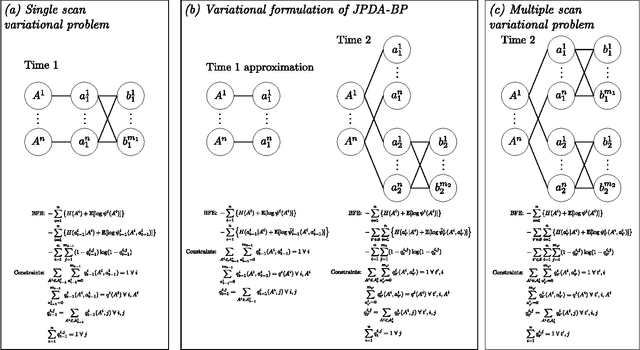
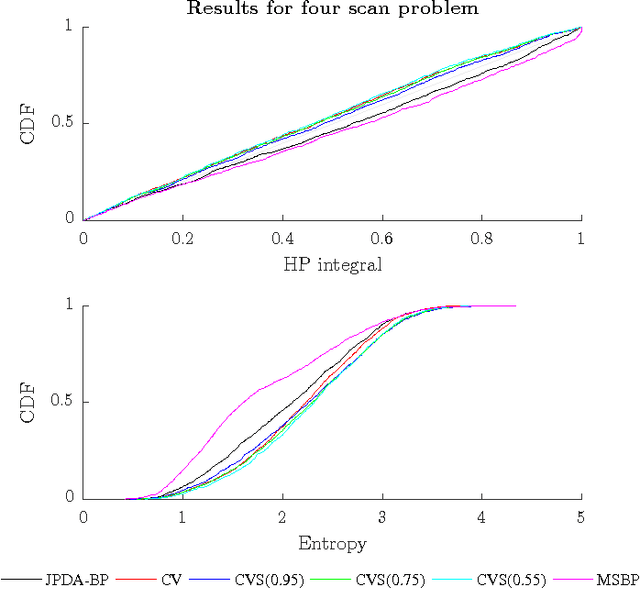
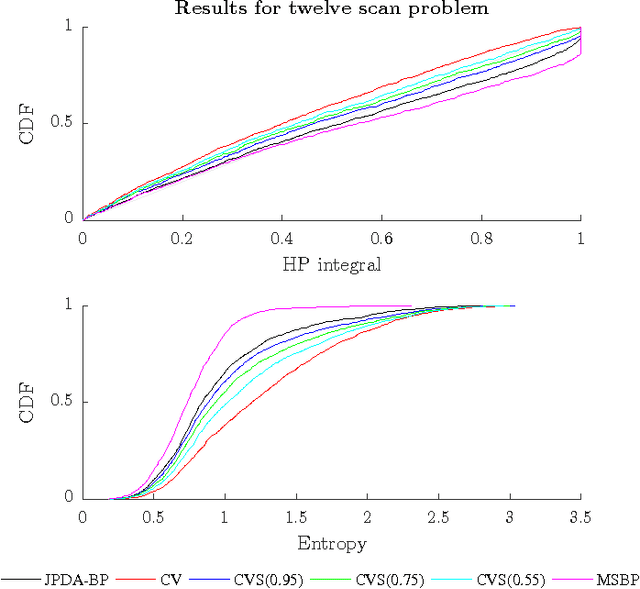
Data association, the reasoning over correspondence between targets and measurements, is a problem of fundamental importance in target tracking. Recently, belief propagation (BP) has emerged as a promising method for estimating the marginal probabilities of measurement to target association, providing fast, accurate estimates. The excellent performance of BP in the particular formulation used may be attributed to the convexity of the underlying free energy which it implicitly optimises. This paper studies multiple scan data association problems, i.e., problems that reason over correspondence between targets and several sets of measurements, which may correspond to different sensors or different time steps. We find that the multiple scan extension of the single scan BP formulation is non-convex and demonstrate the undesirable behaviour that can result. A convex free energy is constructed using the recently proposed fractional free energy (FFE). A convergent, BP-like algorithm is provided for the single scan FFE, and employed in optimising the multiple scan free energy using primal-dual coordinate ascent. Finally, based on a variational interpretation of joint probabilistic data association (JPDA), we develop a sequential variant of the algorithm that is similar to JPDA, but retains consistency constraints from prior scans. The performance of the proposed methods is demonstrated on a bearings only target localisation problem.

Marginal multi-Bernoulli filters: RFS derivation of MHT, JIPDA and association-based MeMBer

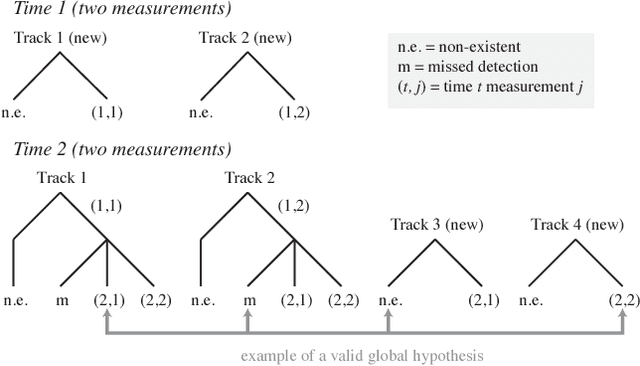
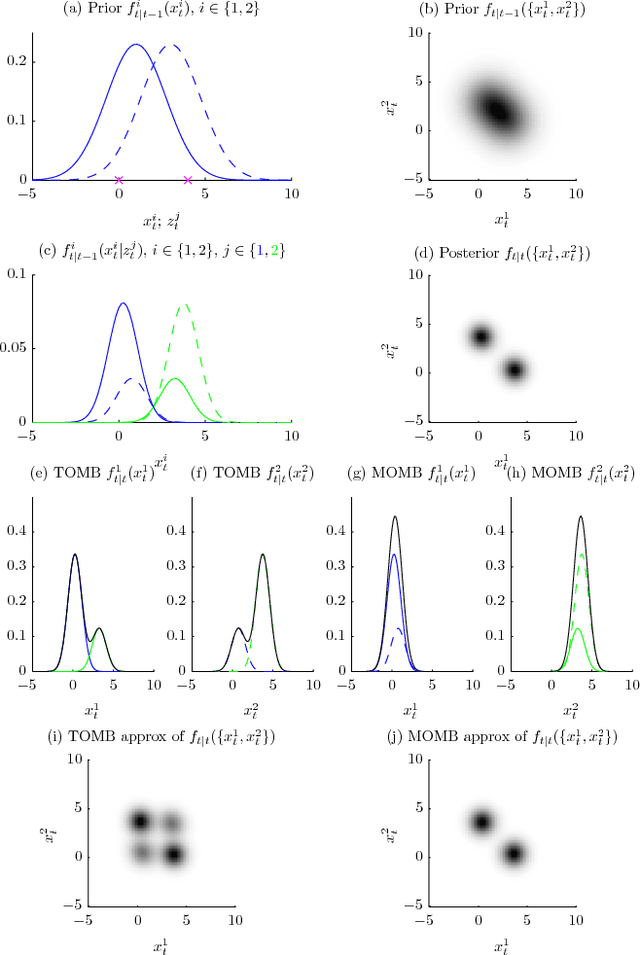
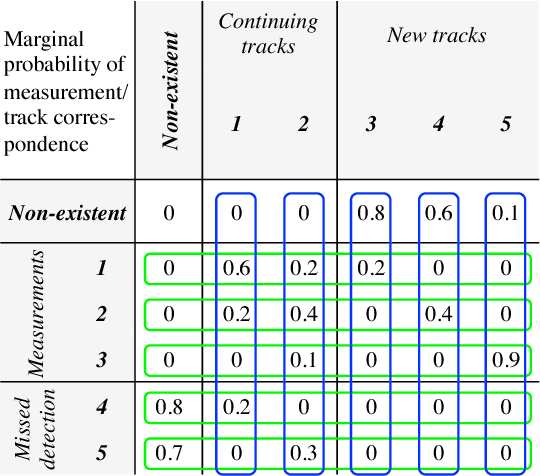
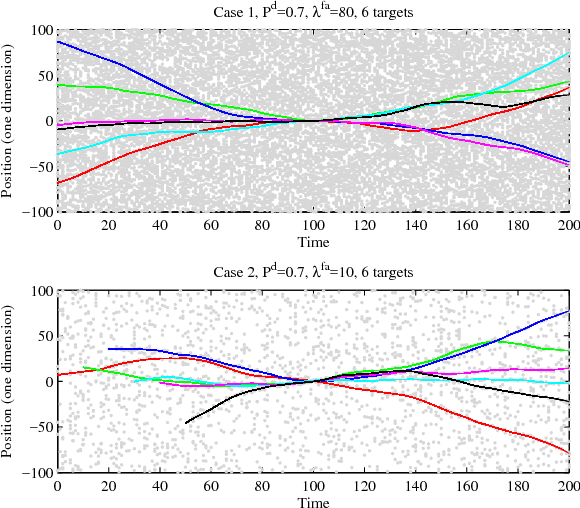
Recent developments in random finite sets (RFSs) have yielded a variety of tracking methods that avoid data association. This paper derives a form of the full Bayes RFS filter and observes that data association is implicitly present, in a data structure similar to MHT. Subsequently, algorithms are obtained by approximating the distribution of associations. Two algorithms result: one nearly identical to JIPDA, and another related to the MeMBer filter. Both improve performance in challenging environments.

Approximate evaluation of marginal association probabilities with belief propagation

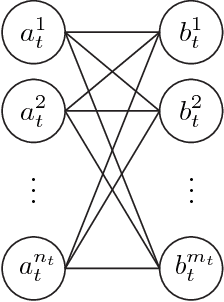
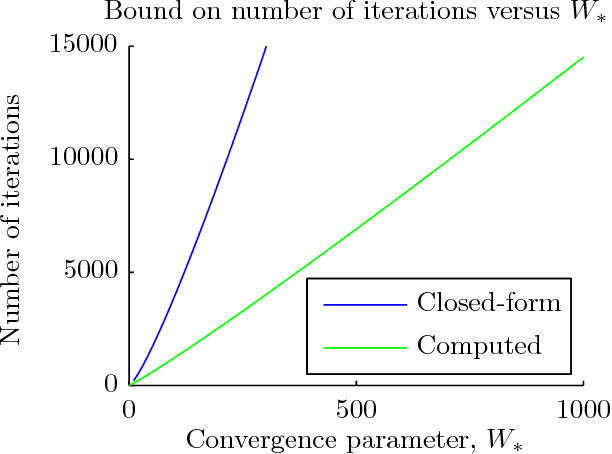
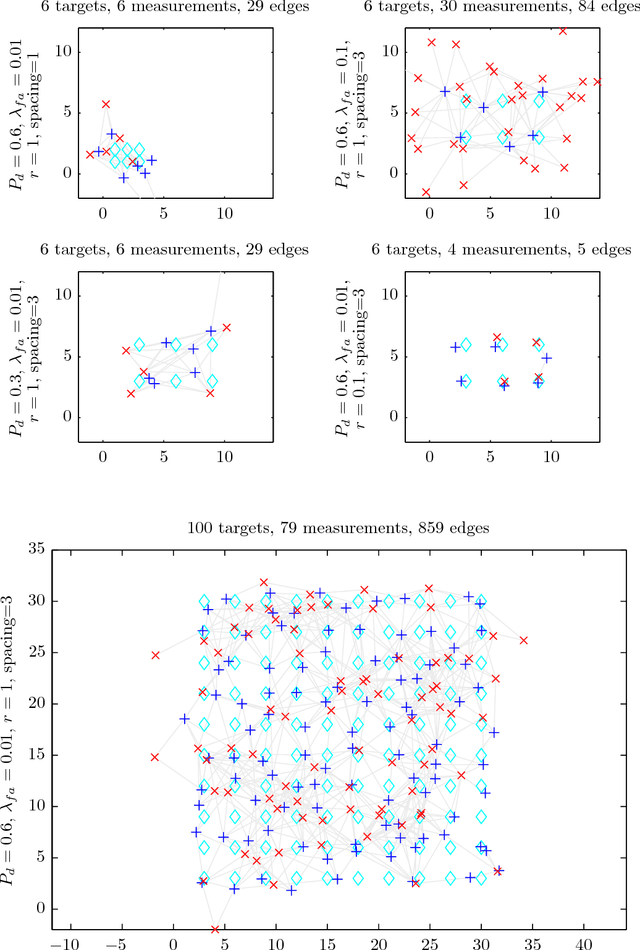
Data association, the problem of reasoning over correspondence between targets and measurements, is a fundamental problem in tracking. This paper presents a graphical model formulation of data association and applies an approximate inference method, belief propagation (BP), to obtain estimates of marginal association probabilities. We prove that BP is guaranteed to converge, and bound the number of iterations necessary. Experiments reveal a favourable comparison to prior methods in terms of accuracy and computational complexity.

Hybrid Poisson and multi-Bernoulli filters

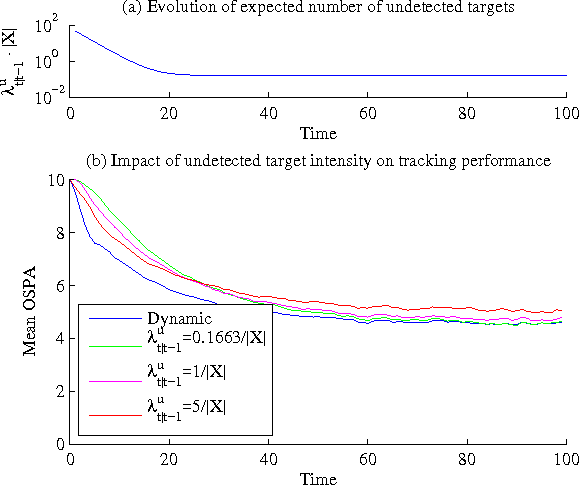
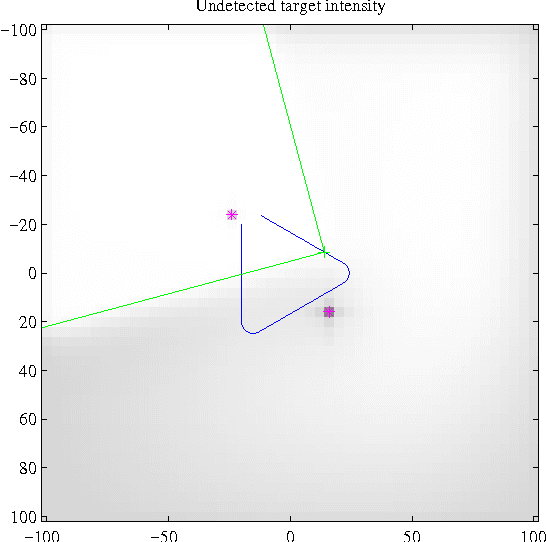
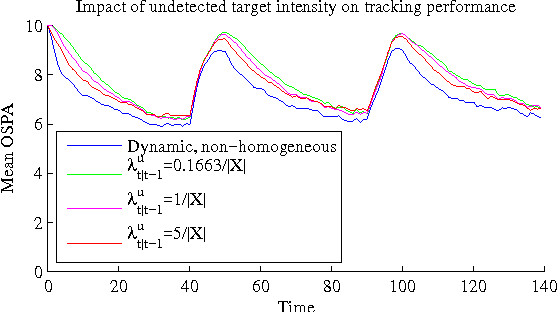
The probability hypothesis density (PHD) and multi-target multi-Bernoulli (MeMBer) filters are two leading algorithms that have emerged from random finite sets (RFS). In this paper we study a method which combines these two approaches. Our work is motivated by a sister paper, which proves that the full Bayes RFS filter naturally incorporates a Poisson component representing targets that have never been detected, and a linear combination of multi-Bernoulli components representing targets under track. Here we demonstrate the benefit (in speed of track initiation) that maintenance of a Poisson component of undetected targets provides. Subsequently, we propose a method of recycling, which projects Bernoulli components with a low probability of existence onto the Poisson component (as opposed to deleting them). We show that this allows us to achieve similar tracking performance using a fraction of the number of Bernoulli components (i.e., tracks).