Evolutionary Discovery of Sequence Acceleration Methods for Slab Geometry Neutron Transport

We present a genetic programming approach to automatically discover convergence acceleration methods for discrete ordinates solutions of neutron transport problems in slab geometry. Classical acceleration methods such as Aitken's delta-squared and Wynn epsilon assume specific convergence patterns and do not generalize well to the broad set of transport problems encountered in practice. We evolved mathematical formulas specifically tailored to SN convergence characteristics in this work. The discovered accelerator, featuring second differences and cross-product terms, achieved over 75 percent success rate in improving convergence compared to raw sequences - almost double that observed for classical techniques for the problem set considered. This work demonstrates the potential for discovering novel numerical methods in computational physics via genetic programming and attempts to honor Prof. Ganapol's legacy of advancing experimental mathematics applied to neutron transport.

Solver Recommendation For Transport Problems in Slabs Using Machine Learning

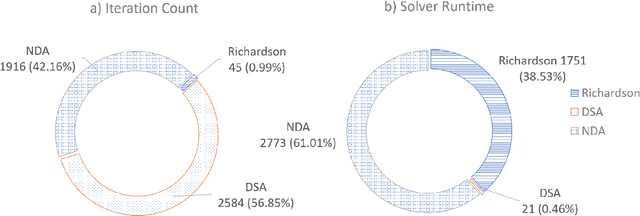
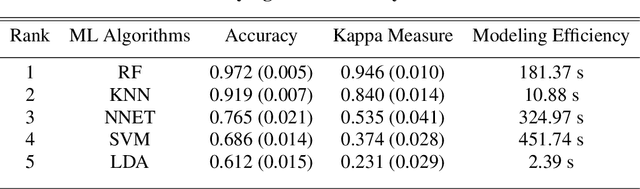
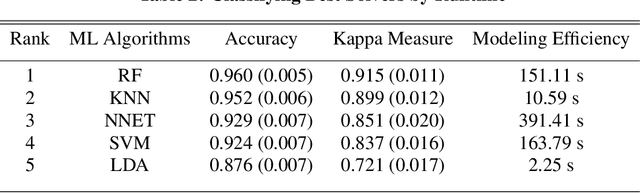
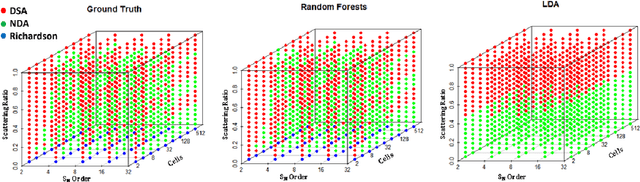
The use of machine learning algorithms to address classification problems is on the rise in many research areas. The current study is aimed at testing the potential of using such algorithms to auto-select the best solvers for transport problems in uniform slabs. Three solvers are used in this work: Richardson, diffusion synthetic acceleration, and nonlinear diffusion acceleration. Three parameters are manipulated to create different transport problem scenarios. Five machine learning algorithms are applied: linear discriminant analysis, K-nearest neighbors, support vector machine, random forest, and neural networks. We present and analyze the results of these algorithms for the test problems, showing that random forest and K-nearest neighbors are potentially the best suited candidates for this type of classification problem.