The Candidate Multi-Cut for Cell Segmentation

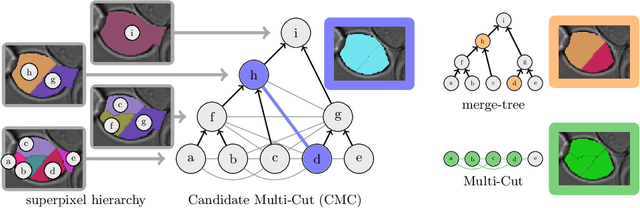
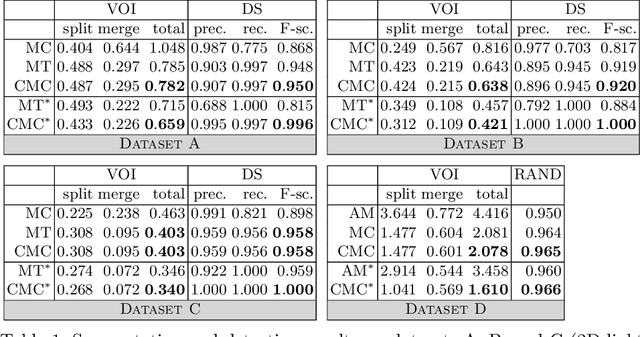
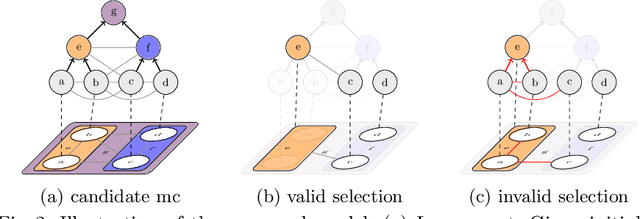
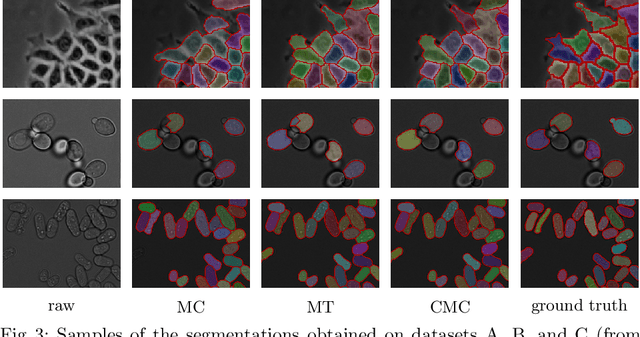
Two successful approaches for the segmentation of biomedical images are (1) the selection of segment candidates from a merge-tree, and (2) the clustering of small superpixels by solving a Multi-Cut problem. In this paper, we introduce a model that unifies both approaches. Our model, the Candidate Multi-Cut (CMC), allows joint selection and clustering of segment candidates from a merge-tree. This way, we overcome the respective limitations of the individual methods: (1) the space of possible segmentations is not constrained to candidates of a merge-tree, and (2) the decision for clustering can be made on candidates larger than superpixels, using features over larger contexts. We solve the optimization problem of selecting and clustering of candidates using an integer linear program. On datasets of 2D light microscopy of cell populations and 3D electron microscopy of neurons, we show that our method generalizes well and generates more accurate segmentations than merge-tree or Multi-Cut methods alone.

TED: A Tolerant Edit Distance for Segmentation Evaluation

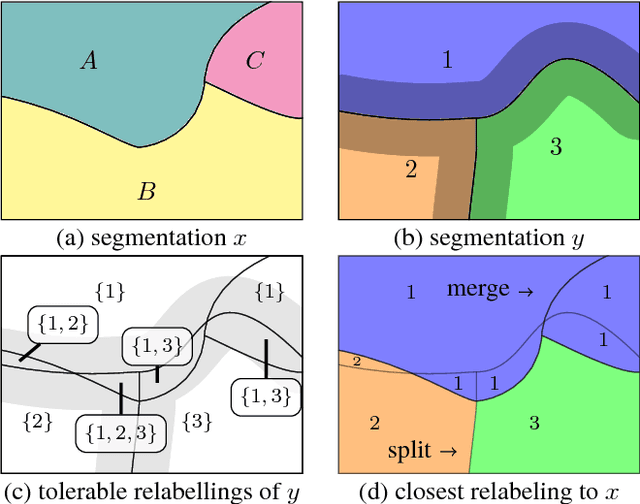
In this paper, we present a novel error measure to compare a segmentation against ground truth. This measure, which we call Tolerant Edit Distance (TED), is motivated by two observations: (1) Some errors, like small boundary shifts, are tolerable in practice. Which errors are tolerable is application dependent and should be a parameter of the measure. (2) Non-tolerable errors have to be corrected manually. The time needed to do so should be reflected by the error measure. Using integer linear programming, the TED finds the minimal weighted sum of split and merge errors exceeding a given tolerance criterion, and thus provides a time-to-fix estimate. In contrast to commonly used measures like Rand index or variation of information, the TED (1) does not count small, but tolerable, differences, (2) provides intuitive numbers, (3) gives a time-to-fix estimate, and (4) can localize and classify the type of errors. By supporting both isotropic and anisotropic volumes and having a flexible tolerance criterion, the TED can be adapted to different requirements. On example segmentations for 3D neuron segmentation, we demonstrate that the TED is capable of counting topological errors, while ignoring small boundary shifts.

Multi-Hypothesis CRF-Segmentation of Neural Tissue in Anisotropic EM Volumes

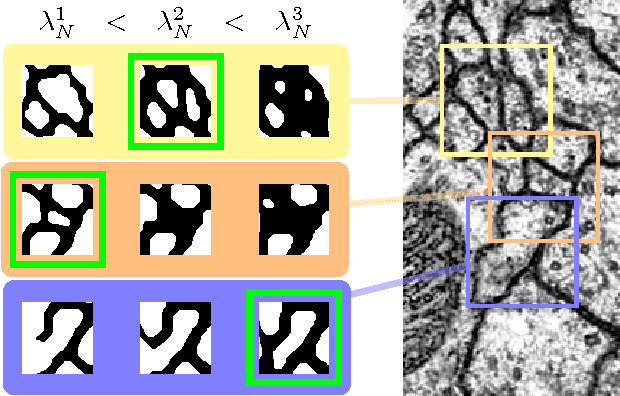
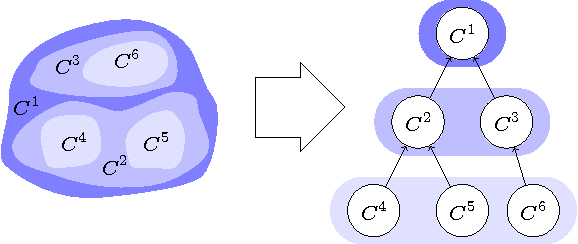
We present an approach for the joint segmentation and grouping of similar components in anisotropic 3D image data and use it to segment neural tissue in serial sections electron microscopy (EM) images. We first construct a nested set of neuron segmentation hypotheses for each slice. A conditional random field (CRF) then allows us to evaluate both the compatibility of a specific segmentation and a specific inter-slice assignment of neuron candidates with the underlying observations. The model is solved optimally for an entire image stack simultaneously using integer linear programming (ILP), which yields the maximum a posteriori solution in amortized linear time in the number of slices. We evaluate the performance of our approach on an annotated sample of the Drosophila larva neuropil and show that the consideration of different segmentation hypotheses in each slice leads to a significant improvement in the segmentation and assignment accuracy.