On Integer Programming for the Binarized Neural Network Verification Problem

Binarized neural networks (BNNs) are feedforward neural networks with binary weights and activation functions. In the context of using a BNN for classification, the verification problem seeks to determine whether a small perturbation of a given input can lead it to be misclassified by the BNN, and the robustness of the BNN can be measured by solving the verification problem over multiple inputs. The BNN verification problem can be formulated as an integer programming (IP) problem. However, the natural IP formulation is often challenging to solve due to a large integrality gap induced by big-$M$ constraints. We present two techniques to improve the IP formulation. First, we introduce a new method for obtaining a linear objective for the multi-class setting. Second, we introduce a new technique for generating valid inequalities for the IP formulation that exploits the recursive structure of BNNs. We find that our techniques enable verifying BNNs against a higher range of input perturbation than existing IP approaches within a limited time.

Data-Driven Sample Average Approximation with Covariate Information

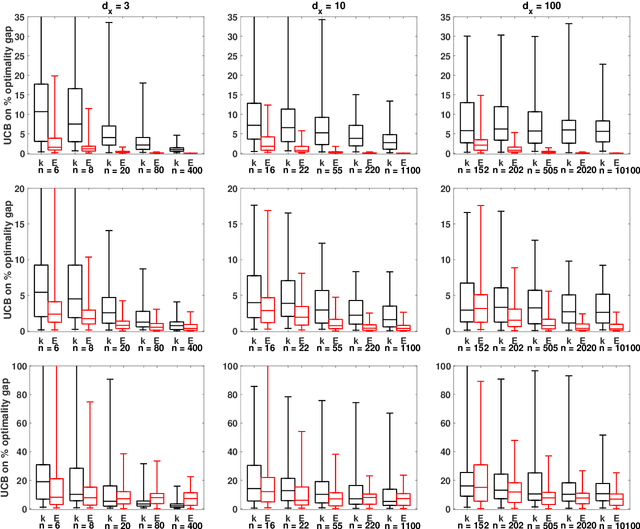
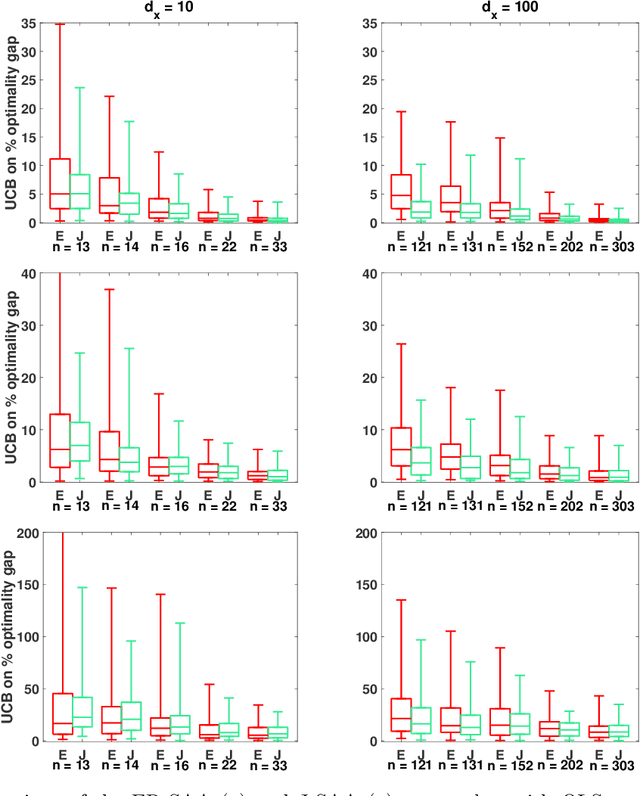
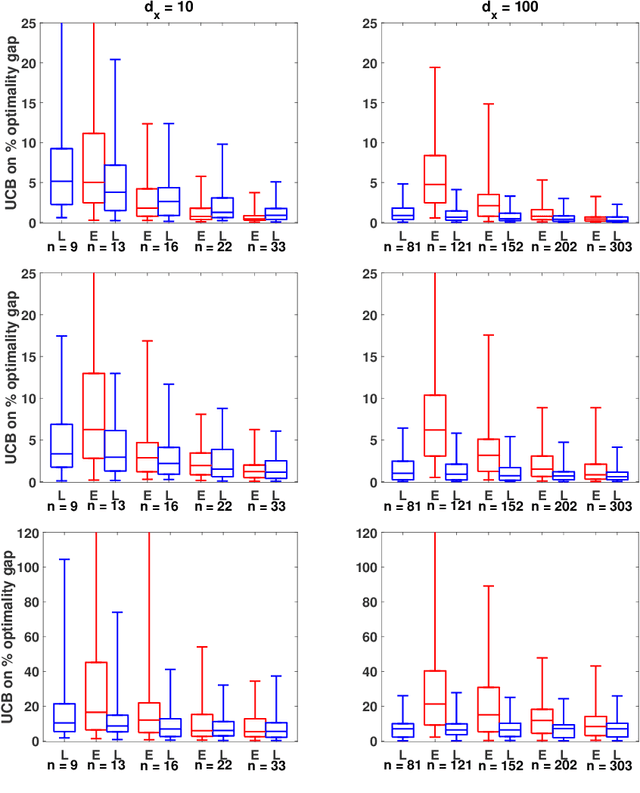
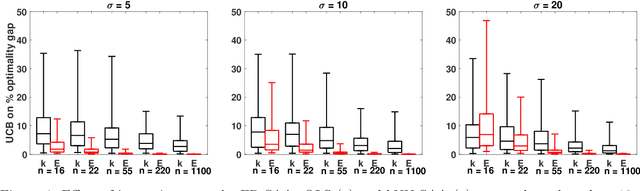
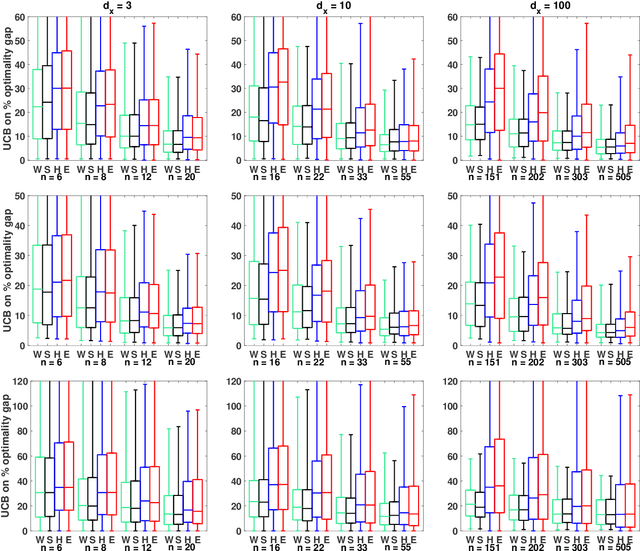
We study optimization for data-driven decision-making when we have observations of the uncertain parameters within the optimization model together with concurrent observations of covariates. Given a new covariate observation, the goal is to choose a decision that minimizes the expected cost conditioned on this observation. We investigate three data-driven frameworks that integrate a machine learning prediction model within a stochastic programming sample average approximation (SAA) for approximating the solution to this problem. Two of the SAA frameworks are new and use out-of-sample residuals of leave-one-out prediction models for scenario generation. The frameworks we investigate are flexible and accommodate parametric, nonparametric, and semiparametric regression techniques. We derive conditions on the data generation process, the prediction model, and the stochastic program under which solutions of these data-driven SAAs are consistent and asymptotically optimal, and also derive convergence rates and finite sample guarantees. Computational experiments validate our theoretical results, demonstrate the potential advantages of our data-driven formulations over existing approaches (even when the prediction model is misspecified), and illustrate the benefits of our new data-driven formulations in the limited data regime.

Residuals-based distributionally robust optimization with covariate information

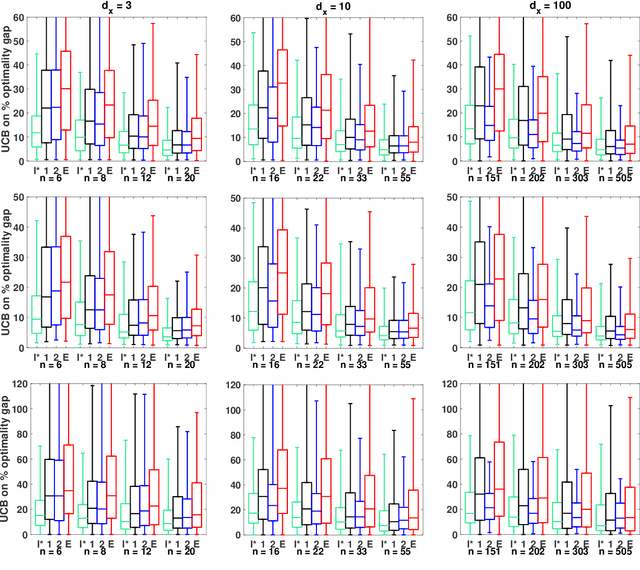
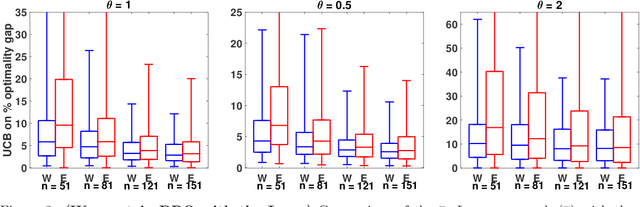
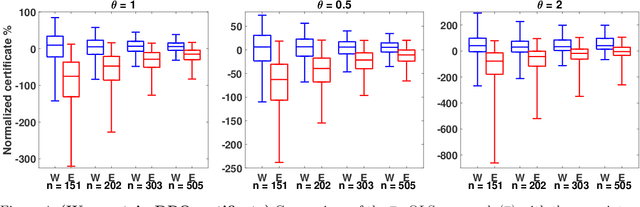
We consider data-driven approaches that integrate a machine learning prediction model within distributionally robust optimization (DRO) given limited joint observations of uncertain parameters and covariates. Our framework is flexible in the sense that it can accommodate a variety of learning setups and DRO ambiguity sets. We investigate the asymptotic and finite sample properties of solutions obtained using Wasserstein, sample robust optimization, and phi-divergence-based ambiguity sets within our DRO formulations, and explore cross-validation approaches for sizing these ambiguity sets. Through numerical experiments, we validate our theoretical results, study the effectiveness of our approaches for sizing ambiguity sets, and illustrate the benefits of our DRO formulations in the limited data regime even when the prediction model is misspecified.