Accelerating Langevin Sampling with Birth-death

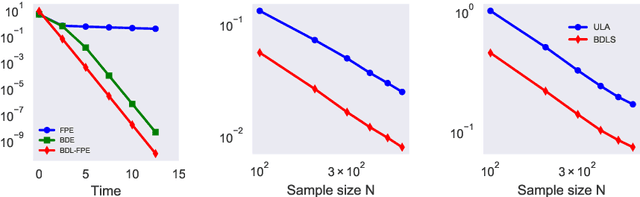
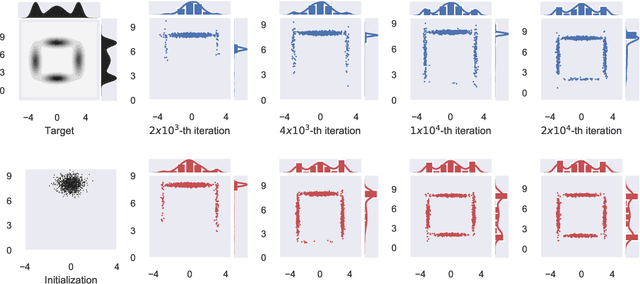
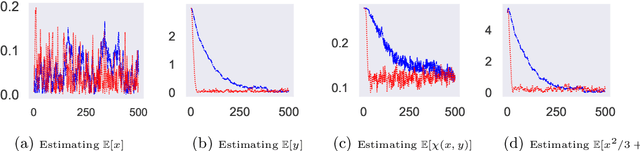
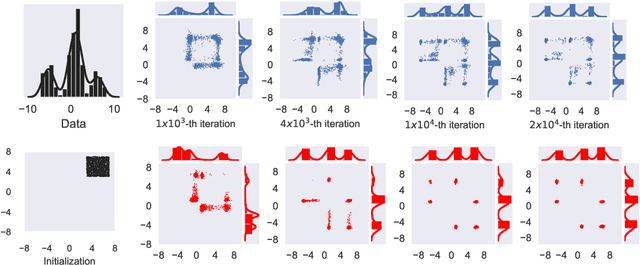
A fundamental problem in Bayesian inference and statistical machine learning is to efficiently sample from multimodal distributions. Due to metastability, multimodal distributions are difficult to sample using standard Markov chain Monte Carlo methods. We propose a new sampling algorithm based on a birth-death mechanism to accelerate the mixing of Langevin diffusion. Our algorithm is motivated by its mean field partial differential equation (PDE), which is a Fokker-Planck equation supplemented by a nonlocal birth-death term. This PDE can be viewed as a gradient flow of the Kullback-Leibler divergence with respect to the Wasserstein-Fisher-Rao metric. We prove that under some assumptions the asymptotic convergence rate of the nonlocal PDE is independent of the potential barrier, in contrast to the exponential dependence in the case of the Langevin diffusion. We illustrate the efficiency of the birth-death accelerated Langevin method through several analytical examples and numerical experiments.

Scaling limit of the Stein variational gradient descent: the mean field regime

We study an interacting particle system in $\mathbf{R}^d$ motivated by Stein variational gradient descent [Q. Liu and D. Wang, NIPS 2016], a deterministic algorithm for sampling from a given probability density with unknown normalization. We prove that in the large particle limit the empirical measure of the particle system converges to a solution of a non-local and nonlinear PDE. We also prove global existence, uniqueness and regularity of the solution to the limiting PDE. Finally, we prove that the solution to the PDE converges to the unique invariant solution in long time limit.