A Unified Optimization Framework for Multiclass Classification with Structured Hyperplane Arrangements

In this paper, we propose a new mathematical optimization model for multiclass classification based on arrangements of hyperplanes. Our approach preserves the core support vector machine (SVM) paradigm of maximizing class separation while minimizing misclassification errors, and it is computationally more efficient than a previous formulation. We present a kernel-based extension that allows it to construct nonlinear decision boundaries. Furthermore, we show how the framework can naturally incorporate alternative geometric structures, including classification trees, $\ell_p$-SVMs, and models with discrete feature selection. To address large-scale instances, we develop a dynamic clustering matheuristic that leverages the proposed MIP formulation. Extensive computational experiments demonstrate the efficiency of the proposed model and dynamic clustering heuristic, and we report competitive classification performance on both synthetic datasets and real-world benchmarks from the UCI Machine Learning Repository, comparing our method with state-of-the-art implementations available in scikit-learn.

Heteroscedasticity-aware residuals-based contextual stochastic optimization

We explore generalizations of some integrated learning and optimization frameworks for data-driven contextual stochastic optimization that can adapt to heteroscedasticity. We identify conditions on the stochastic program, data generation process, and the prediction setup under which these generalizations possess asymptotic and finite sample guarantees for a class of stochastic programs, including two-stage stochastic mixed-integer programs with continuous recourse. We verify that our assumptions hold for popular parametric and nonparametric regression methods.

A stochastic approximation method for chance-constrained nonlinear programs

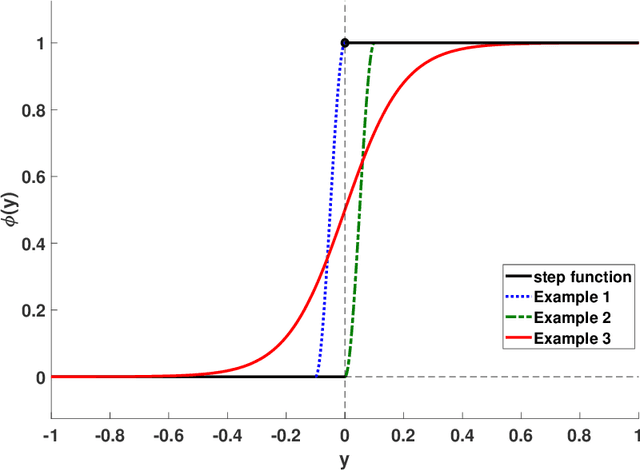
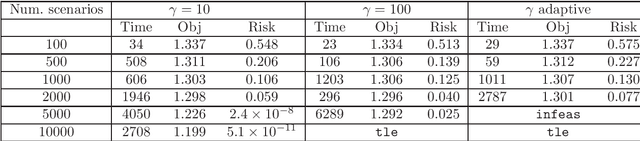
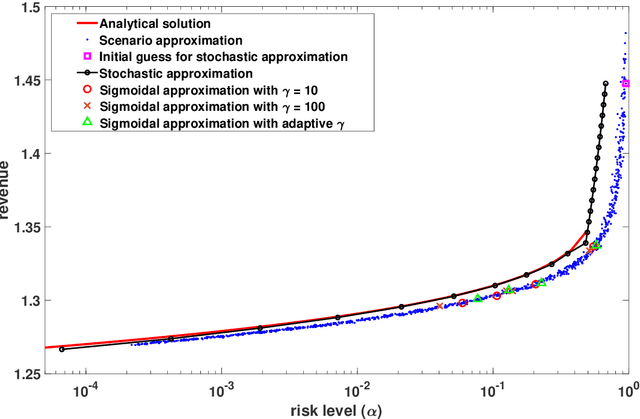
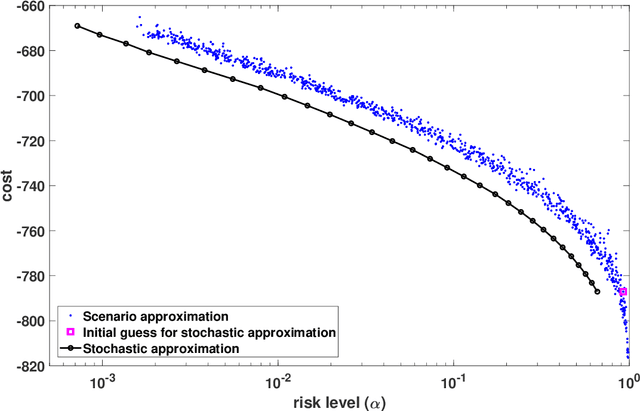
We propose a stochastic approximation method for approximating the efficient frontier of chance-constrained nonlinear programs. Our approach is based on a bi-objective viewpoint of chance-constrained programs that seeks solutions on the efficient frontier of optimal objective value versus risk of constraints violation. In order to be able to apply a projected stochastic subgradient algorithm to solve our reformulation with the probabilistic objective, we adapt existing smoothing-based approaches for chance-constrained problems to derive a convergent sequence of smooth approximations of our reformulated problem. In contrast with exterior sampling-based approaches (such as sample average approximation) that approximate the original chance-constrained program with one having finite support, our proposal converges to local solutions of a smooth approximation of the original problem, thereby avoiding poor local solutions that may be an artefact of a fixed sample. Computational results on three test problems from the literature indicate that our proposal is consistently able to determine better approximations of the efficient frontier than existing approaches in reasonable computation times. We also present a bisection approach for solving chance-constrained programs with a prespecified risk level.