Optimized Architectures for Kolmogorov-Arnold Networks

Efforts to improve Kolmogorov-Arnold networks (KANs) with architectural enhancements have been stymied by the complexity those enhancements bring, undermining the interpretability that makes KANs attractive in the first place. Here we study overprovisioned architectures combined with sparsification to learn compact, interpretable KANs without sacrificing accuracy. Crucially, we focus on differentiable sparsification, turning architecture search into an end-to-end optimization problem. Across function approximation benchmarks, dynamical systems forecasting, and real-world prediction tasks, we demonstrate competitive or superior accuracy while discovering substantially smaller models. Overprovisioning and sparsification are synergistic, with the combination outperforming either alone. The result is a principled path toward models that are both more expressive and more interpretable, addressing a key tension in scientific machine learning.

Evolving Form and Function: Dual-Objective Optimization in Neural Symbolic Regression Networks

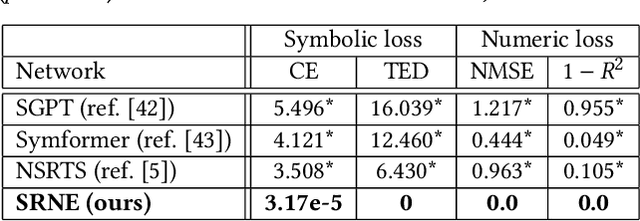
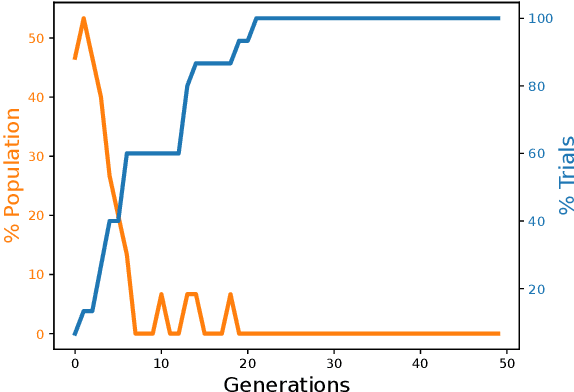
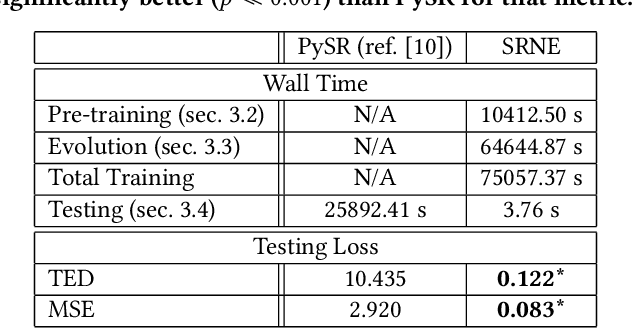
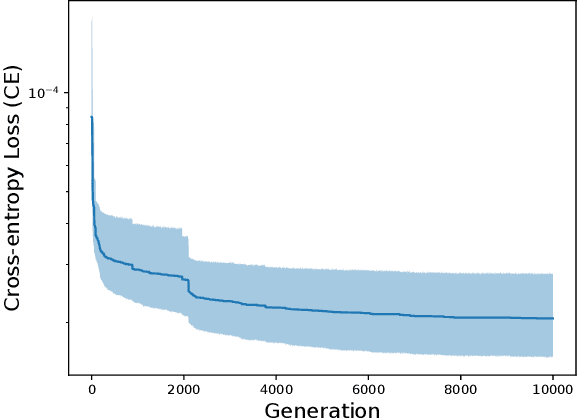
Data increasingly abounds, but distilling their underlying relationships down to something interpretable remains challenging. One approach is genetic programming, which `symbolically regresses' a data set down into an equation. However, symbolic regression (SR) faces the issue of requiring training from scratch for each new dataset. To generalize across all datasets, deep learning techniques have been applied to SR. These networks, however, are only able to be trained using a symbolic objective: NN-generated and target equations are symbolically compared. But this does not consider the predictive power of these equations, which could be measured by a behavioral objective that compares the generated equation's predictions to actual data. Here we introduce a method that combines gradient descent and evolutionary computation to yield neural networks that minimize the symbolic and behavioral errors of the equations they generate from data. As a result, these evolved networks are shown to generate more symbolically and behaviorally accurate equations than those generated by networks trained by state-of-the-art gradient based neural symbolic regression methods. We hope this method suggests that evolutionary algorithms, combined with gradient descent, can improve SR results by yielding equations with more accurate form and function.