Behind the Noise: Conformal Quantile Regression Reveals Emergent Representations

Scientific imaging often involves long acquisition times to obtain high-quality data, especially when probing complex, heterogeneous systems. However, reducing acquisition time to increase throughput inevitably introduces significant noise into the measurements. We present a machine learning approach that not only denoises low-quality measurements with calibrated uncertainty bounds, but also reveals emergent structure in the latent space. By using ensembles of lightweight, randomly structured neural networks trained via conformal quantile regression, our method performs reliable denoising while uncovering interpretable spatial and chemical features -- without requiring labels or segmentation. Unlike conventional approaches focused solely on image restoration, our framework leverages the denoising process itself to drive the emergence of meaningful representations. We validate the approach on real-world geobiochemical imaging data, showing how it supports confident interpretation and guides experimental design under resource constraints.

Advanced Stationary and Non-Stationary Kernel Designs for Domain-Aware Gaussian Processes

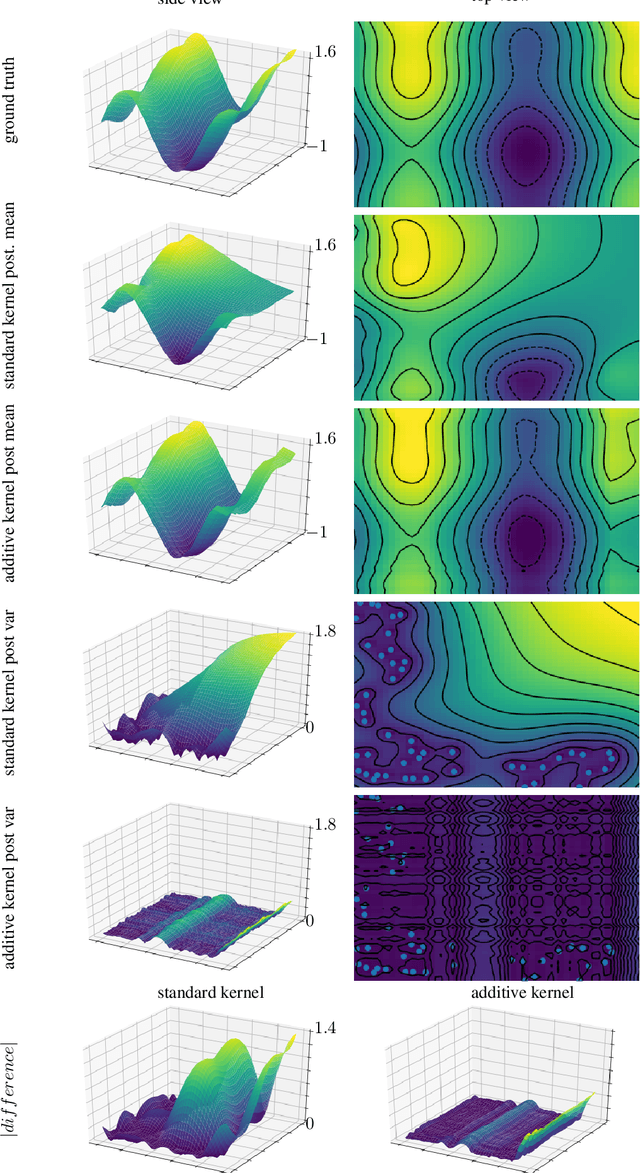
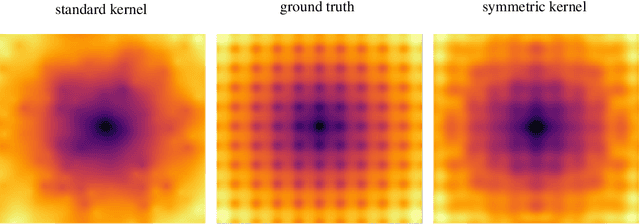
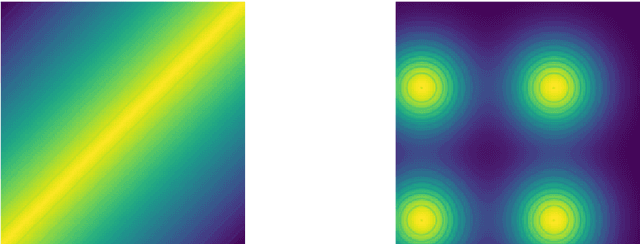
Gaussian process regression is a widely-applied method for function approximation and uncertainty quantification. The technique has gained popularity recently in the machine learning community due to its robustness and interpretability. The mathematical methods we discuss in this paper are an extension of the Gaussian-process framework. We are proposing advanced kernel designs that only allow for functions with certain desirable characteristics to be elements of the reproducing kernel Hilbert space (RKHS) that underlies all kernel methods and serves as the sample space for Gaussian process regression. These desirable characteristics reflect the underlying physics; two obvious examples are symmetry and periodicity constraints. In addition, non-stationary kernel designs can be defined in the same framework to yield flexible multi-task Gaussian processes. We will show the impact of advanced kernel designs on Gaussian processes using several synthetic and two scientific data sets. The results show that including domain knowledge, communicated through advanced kernel designs, has a significant impact on the accuracy and relevance of the function approximation.