Unreasonable effectiveness of unsupervised learning in identifying Majorana topology

In unsupervised learning, the training data for deep learning does not come with any labels, thus forcing the algorithm to discover hidden patterns in the data for discerning useful information. This, in principle, could be a powerful tool in identifying topological order since topology does not always manifest in obvious physical ways (e.g., topological superconductivity) for its decisive confirmation. The problem, however, is that unsupervised learning is a difficult challenge, necessitating huge computing resources, which may not always work. In the current work, we combine unsupervised and supervised learning using an autoencoder to establish that unlabeled data in the Majorana splitting in realistic short disordered nanowires may enable not only a distinction between `topological' and `trivial', but also where their crossover happens in the relevant parameter space. This may be a useful tool in identifying topology in Majorana nanowires.

Derandomized shallow shadows: Efficient Pauli learning with bounded-depth circuits

Efficiently estimating large numbers of non-commuting observables is an important subroutine of many quantum science tasks. We present the derandomized shallow shadows (DSS) algorithm for efficiently learning a large set of non-commuting observables, using shallow circuits to rotate into measurement bases. Exploiting tensor network techniques to ensure polynomial scaling of classical resources, our algorithm outputs a set of shallow measurement circuits that approximately minimizes the sample complexity of estimating a given set of Pauli strings. We numerically demonstrate systematic improvement, in comparison with state-of-the-art techniques, for energy estimation of quantum chemistry benchmarks and verification of quantum many-body systems, and we observe DSS's performance consistently improves as one allows deeper measurement circuits. These results indicate that in addition to being an efficient, low-depth, stand-alone algorithm, DSS can also benefit many larger quantum algorithms requiring estimation of multiple non-commuting observables.

An active inference model of collective intelligence

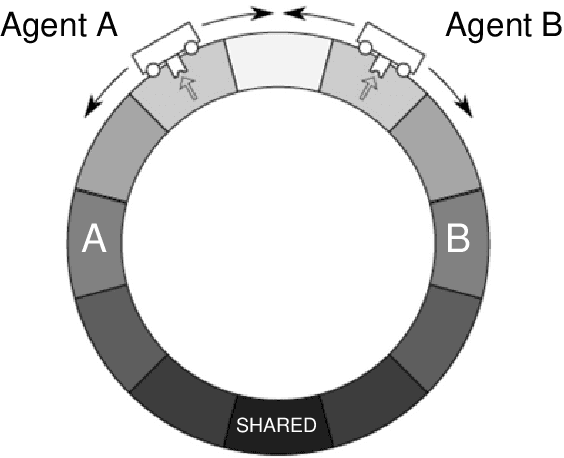
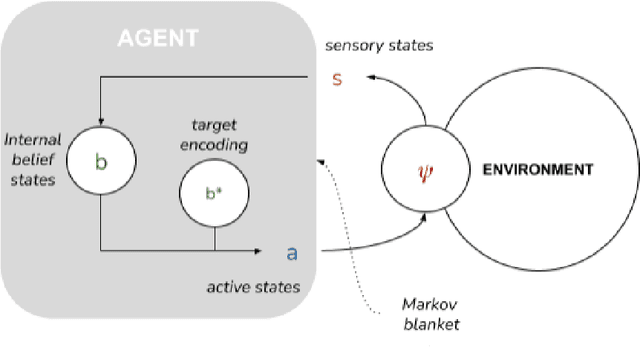
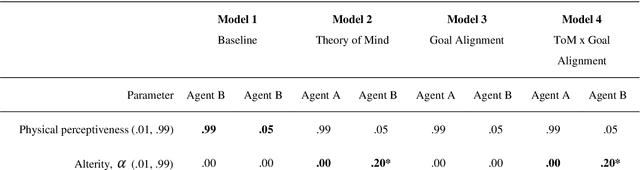
To date, formal models of collective intelligence have lacked a plausible mathematical description of the relationship between local-scale interactions between highly autonomous sub-system components (individuals) and global-scale behavior of the composite system (the collective). In this paper we use the Active Inference Formulation (AIF), a framework for explaining the behavior of any non-equilibrium steady state system at any scale, to posit a minimal agent-based model that simulates the relationship between local individual-level interaction and collective intelligence (operationalized as system-level performance). We explore the effects of providing baseline AIF agents (Model 1) with specific cognitive capabilities: Theory of Mind (Model 2); Goal Alignment (Model 3), and Theory of Mind with Goal Alignment (Model 4). These stepwise transitions in sophistication of cognitive ability are motivated by the types of advancements plausibly required for an AIF agent to persist and flourish in an environment populated by other AIF agents, and have also recently been shown to map naturally to canonical steps in human cognitive ability. Illustrative results show that stepwise cognitive transitions increase system performance by providing complementary mechanisms for alignment between agents' local and global optima. Alignment emerges endogenously from the dynamics of interacting AIF agents themselves, rather than being imposed exogenously by incentives to agents' behaviors (contra existing computational models of collective intelligence) or top-down priors for collective behavior (contra existing multiscale simulations of AIF). These results shed light on the types of generic information-theoretic patterns conducive to collective intelligence in human and other complex adaptive systems.