Deep Symbolic Optimization: Reinforcement Learning for Symbolic Mathematics

Deep Symbolic Optimization (DSO) is a novel computational framework that enables symbolic optimization for scientific discovery, particularly in applications involving the search for intricate symbolic structures. One notable example is equation discovery, which aims to automatically derive mathematical models expressed in symbolic form. In DSO, the discovery process is formulated as a sequential decision-making task. A generative neural network learns a probabilistic model over a vast space of candidate symbolic expressions, while reinforcement learning strategies guide the search toward the most promising regions. This approach integrates gradient-based optimization with evolutionary and local search techniques, and it incorporates in-situ constraints, domain-specific priors, and advanced policy optimization methods. The result is a robust framework capable of efficiently exploring extensive search spaces to identify interpretable and physically meaningful models. Extensive evaluations on benchmark problems have demonstrated that DSO achieves state-of-the-art performance in both accuracy and interpretability. In this chapter, we provide a comprehensive overview of the DSO framework and illustrate its transformative potential for automating symbolic optimization in scientific discovery.

DisCo-DSO: Coupling Discrete and Continuous Optimization for Efficient Generative Design in Hybrid Spaces

We consider the challenge of black-box optimization within hybrid discrete-continuous and variable-length spaces, a problem that arises in various applications, such as decision tree learning and symbolic regression. We propose DisCo-DSO (Discrete-Continuous Deep Symbolic Optimization), a novel approach that uses a generative model to learn a joint distribution over discrete and continuous design variables to sample new hybrid designs. In contrast to standard decoupled approaches, in which the discrete and continuous variables are optimized separately, our joint optimization approach uses fewer objective function evaluations, is robust against non-differentiable objectives, and learns from prior samples to guide the search, leading to significant improvement in performance and sample efficiency. Our experiments on a diverse set of optimization tasks demonstrate that the advantages of DisCo-DSO become increasingly evident as the complexity of the problem increases. In particular, we illustrate DisCo-DSO's superiority over the state-of-the-art methods for interpretable reinforcement learning with decision trees.

Improving exploration in policy gradient search: Application to symbolic optimization

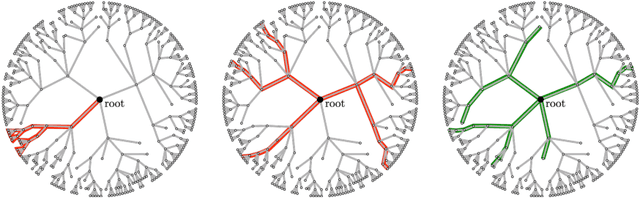
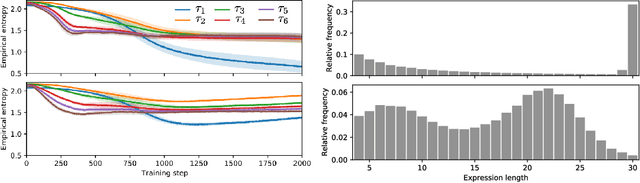
Many machine learning strategies designed to automate mathematical tasks leverage neural networks to search large combinatorial spaces of mathematical symbols. In contrast to traditional evolutionary approaches, using a neural network at the core of the search allows learning higher-level symbolic patterns, providing an informed direction to guide the search. When no labeled data is available, such networks can still be trained using reinforcement learning. However, we demonstrate that this approach can suffer from an early commitment phenomenon and from initialization bias, both of which limit exploration. We present two exploration methods to tackle these issues, building upon ideas of entropy regularization and distribution initialization. We show that these techniques can improve the performance, increase sample efficiency, and lower the complexity of solutions for the task of symbolic regression.