Automatic Differentiation to Simultaneously Identify Nonlinear Dynamics and Extract Noise Probability Distributions from Data

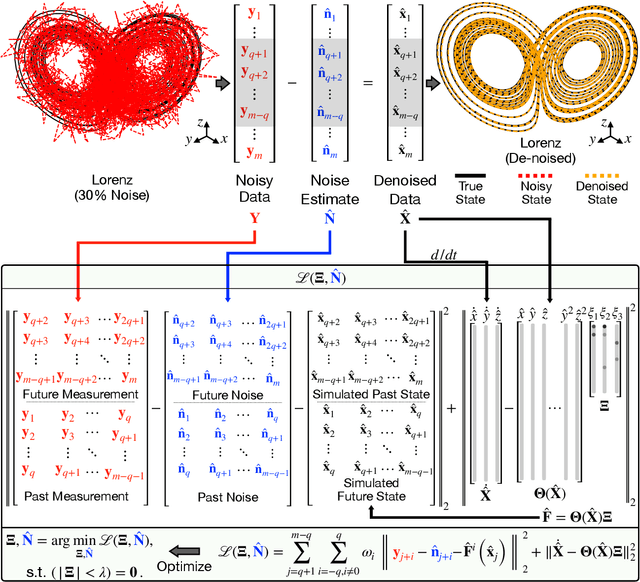
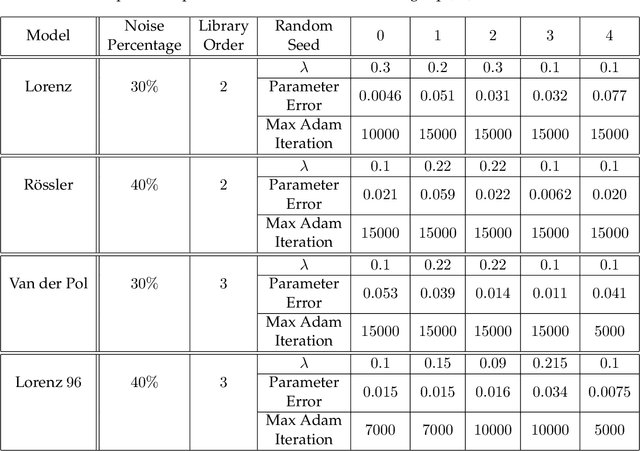
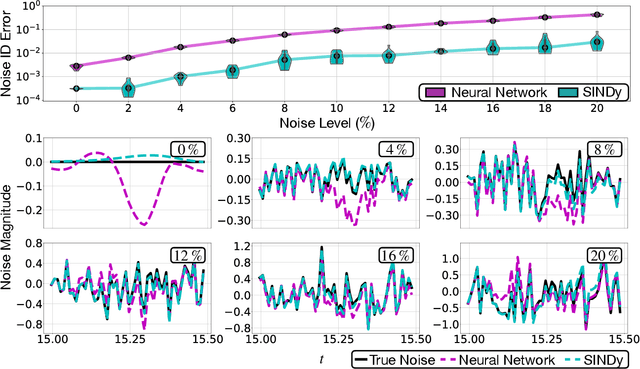
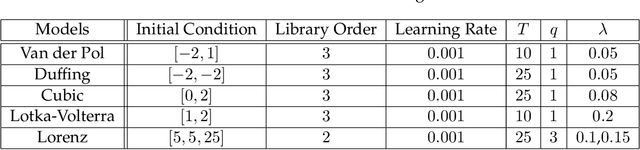
The sparse identification of nonlinear dynamics (SINDy) is a regression framework for the discovery of parsimonious dynamic models and governing equations from time-series data. As with all system identification methods, noisy measurements compromise the accuracy and robustness of the model discovery procedure. In this work, we develop a variant of the SINDy algorithm that integrates automatic differentiation and recent time-stepping constrained motivated by Rudy et al. for simultaneously (i) denoising the data, (ii) learning and parametrizing the noise probability distribution, and (iii) identifying the underlying parsimonious dynamical system responsible for generating the time-series data. Thus within an integrated optimization framework, noise can be separated from signal, resulting in an architecture that is approximately twice as robust to noise as state-of-the-art methods, handling as much as 40% noise on a given time-series signal and explicitly parametrizing the noise probability distribution. We demonstrate this approach on several numerical examples, from Lotka-Volterra models to the spatio-temporal Lorenz 96 model. Further, we show the method can identify a diversity of probability distributions including Gaussian, uniform, Gamma, and Rayleigh.

Data-Driven Aerospace Engineering: Reframing the Industry with Machine Learning

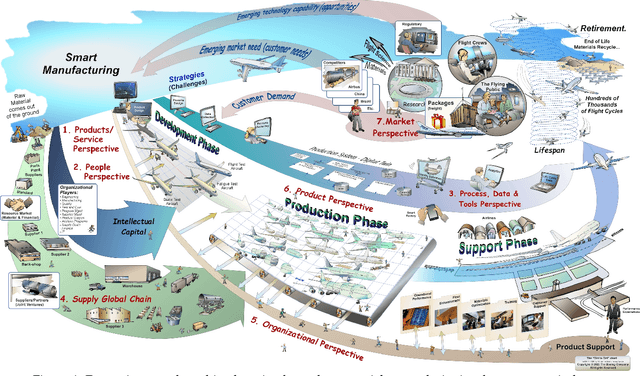
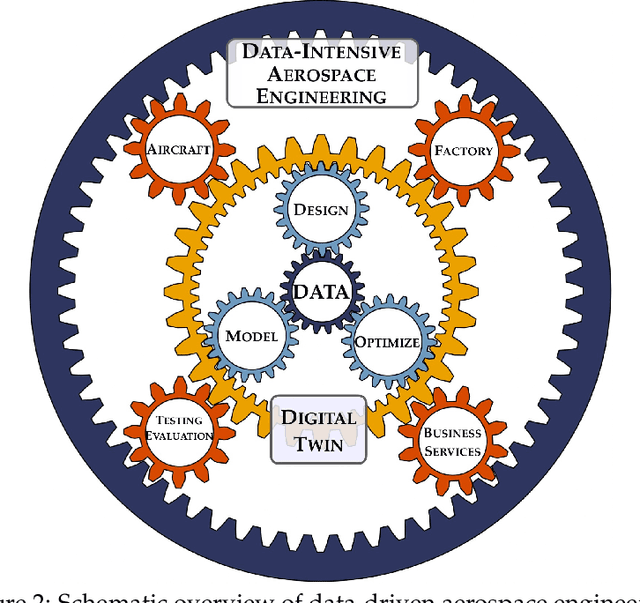
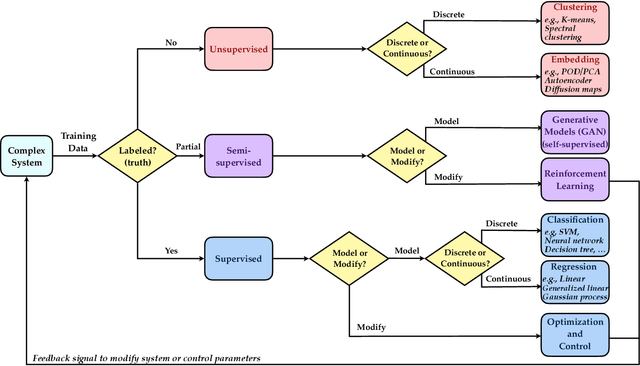
Data science, and machine learning in particular, is rapidly transforming the scientific and industrial landscapes. The aerospace industry is poised to capitalize on big data and machine learning, which excels at solving the types of multi-objective, constrained optimization problems that arise in aircraft design and manufacturing. Indeed, emerging methods in machine learning may be thought of as data-driven optimization techniques that are ideal for high-dimensional, non-convex, and constrained, multi-objective optimization problems, and that improve with increasing volumes of data. In this review, we will explore the opportunities and challenges of integrating data-driven science and engineering into the aerospace industry. Importantly, we will focus on the critical need for interpretable, generalizeable, explainable, and certifiable machine learning techniques for safety-critical applications. This review will include a retrospective, an assessment of the current state-of-the-art, and a roadmap looking forward. Recent algorithmic and technological trends will be explored in the context of critical challenges in aerospace design, manufacturing, verification, validation, and services. In addition, we will explore this landscape through several case studies in the aerospace industry. This document is the result of close collaboration between UW and Boeing to summarize past efforts and outline future opportunities.

Hierarchical Deep Learning of Multiscale Differential Equation Time-Steppers

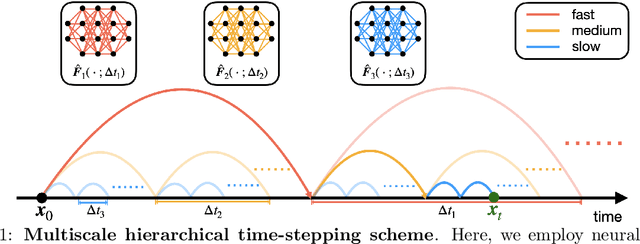
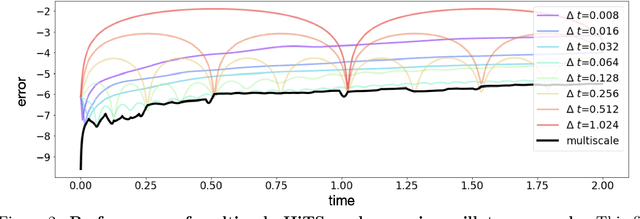
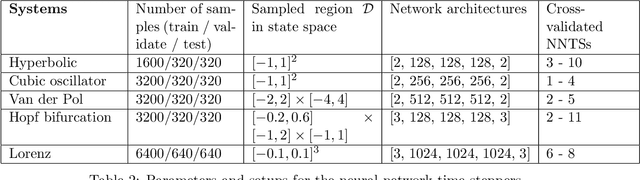
Nonlinear differential equations rarely admit closed-form solutions, thus requiring numerical time-stepping algorithms to approximate solutions. Further, many systems characterized by multiscale physics exhibit dynamics over a vast range of timescales, making numerical integration computationally expensive due to numerical stiffness. In this work, we develop a hierarchy of deep neural network time-steppers to approximate the flow map of the dynamical system over a disparate range of time-scales. The resulting model is purely data-driven and leverages features of the multiscale dynamics, enabling numerical integration and forecasting that is both accurate and highly efficient. Moreover, similar ideas can be used to couple neural network-based models with classical numerical time-steppers. Our multiscale hierarchical time-stepping scheme provides important advantages over current time-stepping algorithms, including (i) circumventing numerical stiffness due to disparate time-scales, (ii) improved accuracy in comparison with leading neural-network architectures, (iii) efficiency in long-time simulation/forecasting due to explicit training of slow time-scale dynamics, and (iv) a flexible framework that is parallelizable and may be integrated with standard numerical time-stepping algorithms. The method is demonstrated on a wide range of nonlinear dynamical systems, including the Van der Pol oscillator, the Lorenz system, the Kuramoto-Sivashinsky equation, and fluid flow pass a cylinder; audio and video signals are also explored. On the sequence generation examples, we benchmark our algorithm against state-of-the-art methods, such as LSTM, reservoir computing, and clockwork RNN. Despite the structural simplicity of our method, it outperforms competing methods on numerical integration.

Bracketing brackets with bras and kets

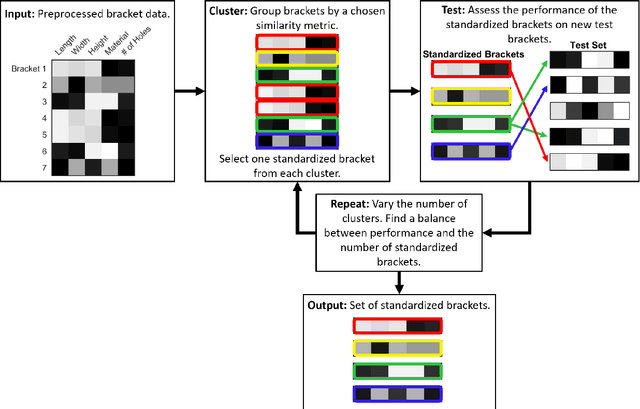
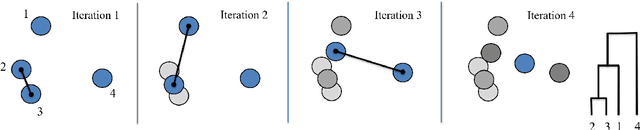
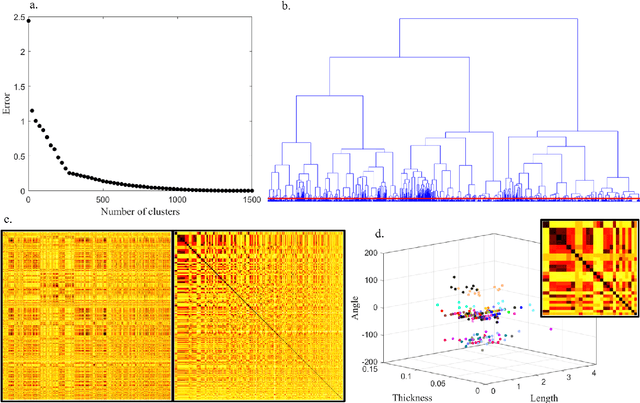
Brackets are an essential component in aircraft manufacture and design, joining parts together, supporting weight, holding wires, and strengthening joints. Hundreds or thousands of unique brackets are used in every aircraft, but manufacturing a large number of distinct brackets is inefficient and expensive. Fortunately, many so-called "different" brackets are in fact very similar or even identical to each other. In this manuscript, we present a data-driven framework for constructing a comparatively small group of representative brackets from a large catalog of current brackets, based on hierarchical clustering of bracket data. We find that for a modern commercial aircraft, the full set of brackets can be reduced by 30\% while still describing half of the test set sufficiently accurately. This approach is based on designing an inner product that quantifies a multi-objective similarity between two brackets, which are the "bra" and the "ket" of the inner product. Although we demonstrate this algorithm to reduce the number of brackets in aerospace manufacturing, it may be generally applied to any large-scale component standardization effort.

Sparse Identification of Slow Timescale Dynamics

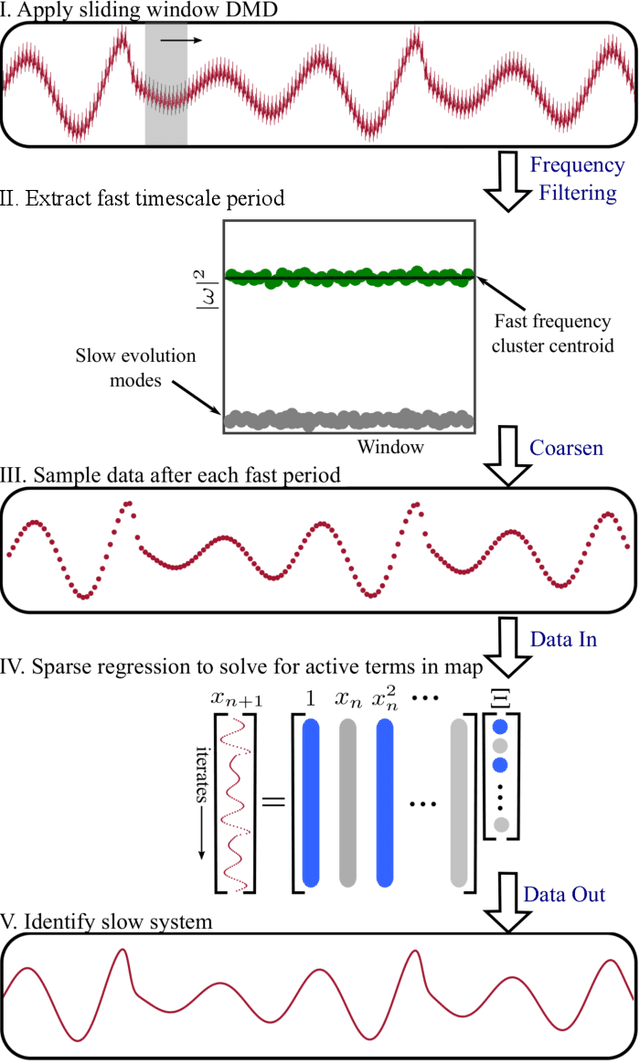
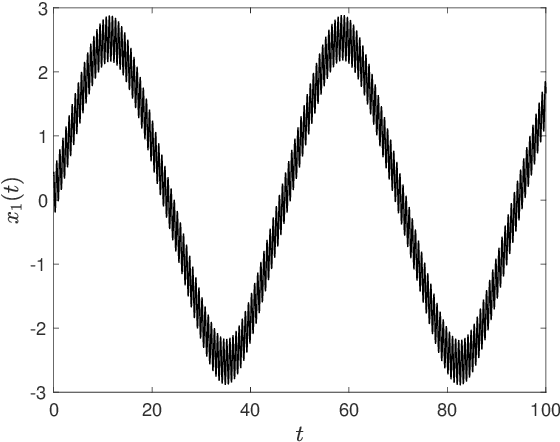
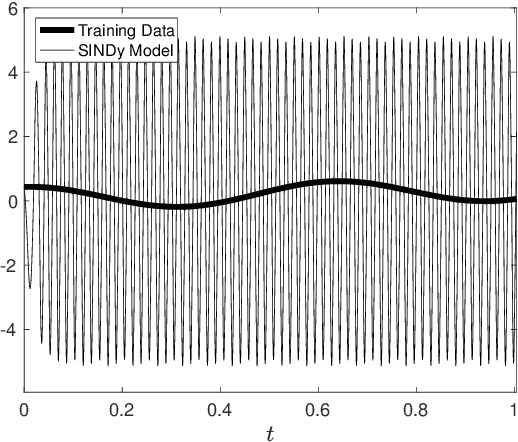
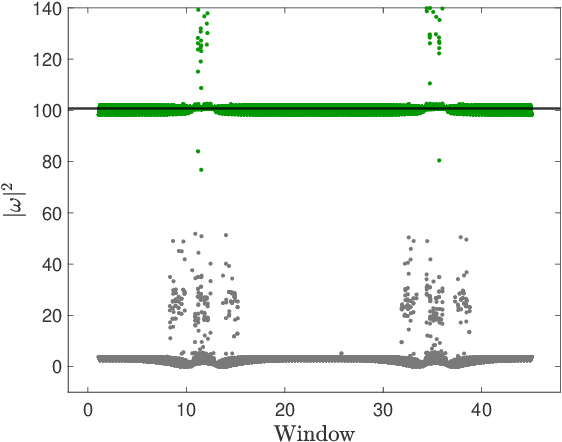
Multiscale phenomena that evolve on multiple distinct timescales are prevalent throughout the sciences. It is often the case that the governing equations of the persistent and approximately periodic fast scales are prescribed, while the emergent slow scale evolution is unknown. Yet the course-grained, slow scale dynamics is often of greatest interest in practice. In this work we present an accurate and efficient method for extracting the slow timescale dynamics from a signal exhibiting multiple timescales. The method relies on tracking the signal at evenly-spaced intervals with length given by the period of the fast timescale, which is discovered using clustering techniques in conjunction with the dynamic mode decomposition. Sparse regression techniques are then used to discover a mapping which describes iterations from one data point to the next. We show that for sufficiently disparate timescales this discovered mapping can be used to discover the continuous-time slow dynamics, thus providing a novel tool for extracting dynamics on multiple timescales.

Multiresolution Convolutional Autoencoders

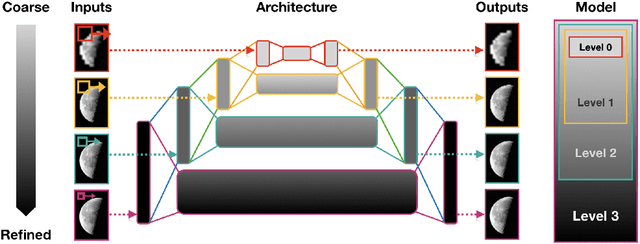
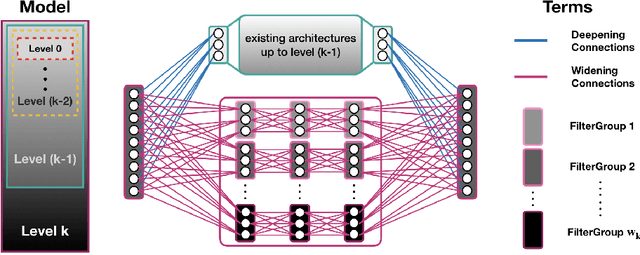
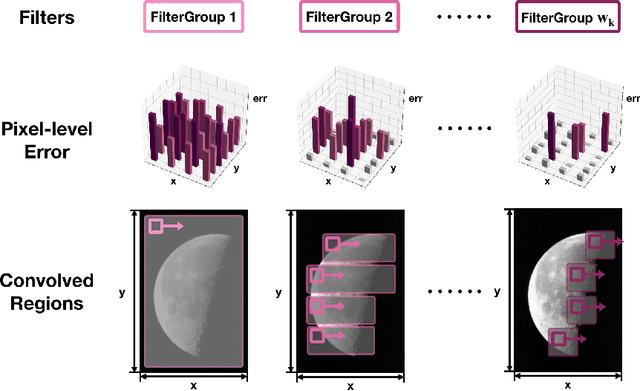
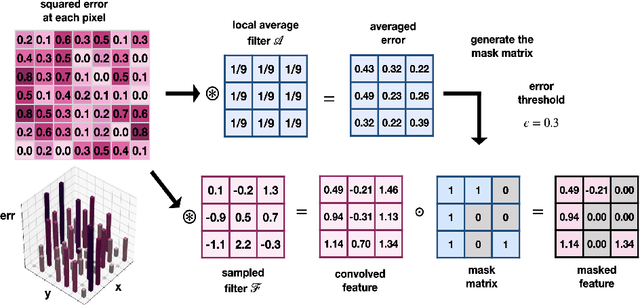
We propose a multi-resolution convolutional autoencoder (MrCAE) architecture that integrates and leverages three highly successful mathematical architectures: (i) multigrid methods, (ii) convolutional autoencoders and (iii) transfer learning. The method provides an adaptive, hierarchical architecture that capitalizes on a progressive training approach for multiscale spatio-temporal data. This framework allows for inputs across multiple scales: starting from a compact (small number of weights) network architecture and low-resolution data, our network progressively deepens and widens itself in a principled manner to encode new information in the higher resolution data based on its current performance of reconstruction. Basic transfer learning techniques are applied to ensure information learned from previous training steps can be rapidly transferred to the larger network. As a result, the network can dynamically capture different scaled features at different depths of the network. The performance gains of this adaptive multiscale architecture are illustrated through a sequence of numerical experiments on synthetic examples and real-world spatial-temporal data.

SINDy-PI: A Robust Algorithm for Parallel Implicit Sparse Identification of Nonlinear Dynamics

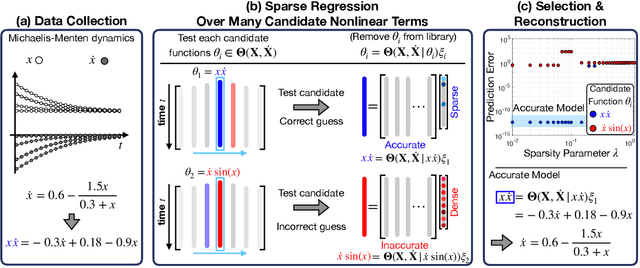
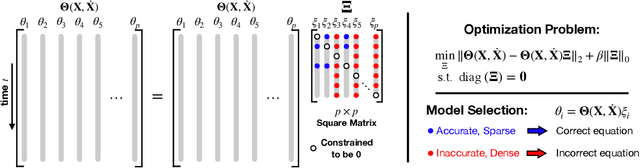
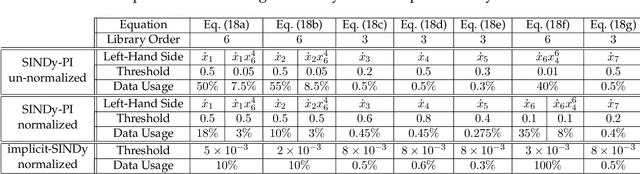
Accurately modeling the nonlinear dynamics of a system from measurement data is a challenging yet vital topic. The sparse identification of nonlinear dynamics (SINDy) algorithm is one approach to discover dynamical systems models from data. Although extensions have been developed to identify implicit dynamics, or dynamics described by rational functions, these extensions are extremely sensitive to noise. In this work, we develop SINDy-PI (parallel, implicit), a robust variant of the SINDy algorithm to identify implicit dynamics and rational nonlinearities. The SINDy-PI framework includes multiple optimization algorithms and a principled approach to model selection. We demonstrate the ability of this algorithm to learn implicit ordinary and partial differential equations and conservation laws from limited and noisy data. In particular, we show that the proposed approach is several orders of magnitude more noise robust than previous approaches, and may be used to identify a class of complex ODE and PDE dynamics that were previously unattainable with SINDy, including for the double pendulum dynamics and the Belousov Zhabotinsky (BZ) reaction.

Deep Learning Models for Global Coordinate Transformations that Linearize PDEs

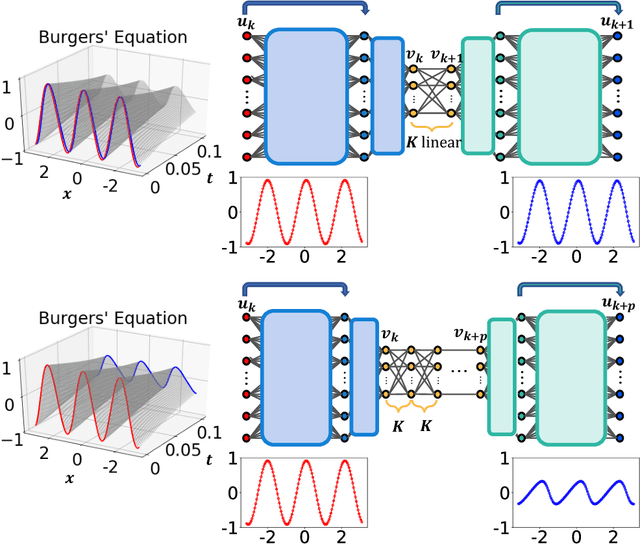
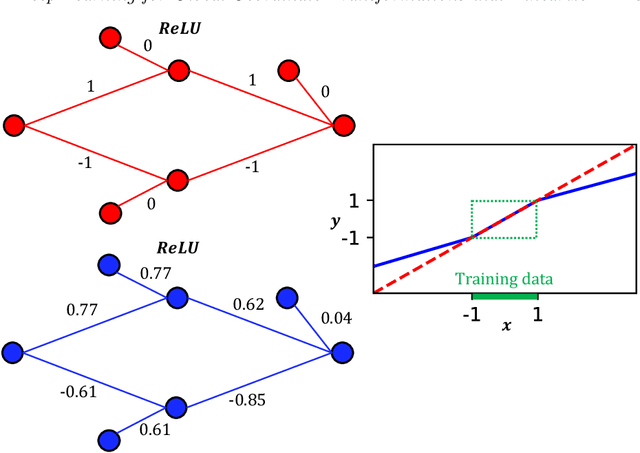
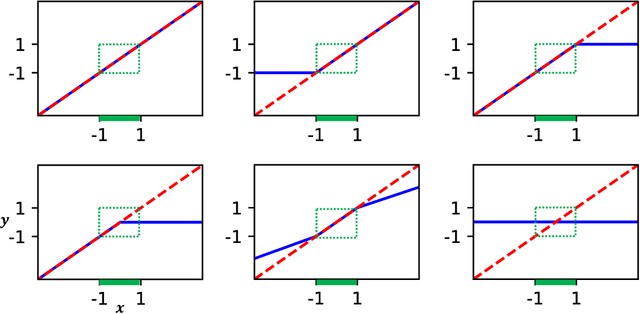
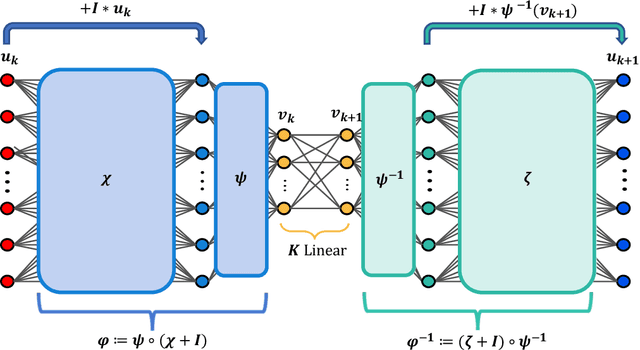
We develop a deep autoencoder architecture that can be used to find a coordinate transformation which turns a nonlinear PDE into a linear PDE. Our architecture is motivated by the linearizing transformations provided by the Cole-Hopf transform for Burgers equation and the inverse scattering transform for completely integrable PDEs. By leveraging a residual network architecture, a near-identity transformation can be exploited to encode intrinsic coordinates in which the dynamics are linear. The resulting dynamics are given by a Koopman operator matrix $\mathbf{K}$. The decoder allows us to transform back to the original coordinates as well. Multiple time step prediction can be performed by repeated multiplication by the matrix $\mathbf{K}$ in the intrinsic coordinates. We demonstrate our method on a number of examples, including the heat equation and Burgers equation, as well as the substantially more challenging Kuramoto-Sivashinsky equation, showing that our method provides a robust architecture for discovering interpretable, linearizing transforms for nonlinear PDEs.

Learning Discrepancy Models From Experimental Data

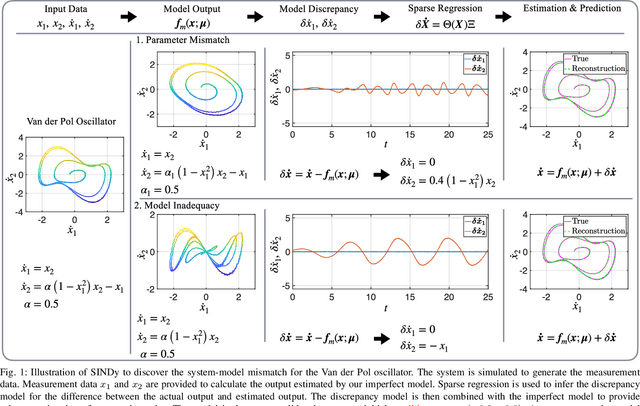
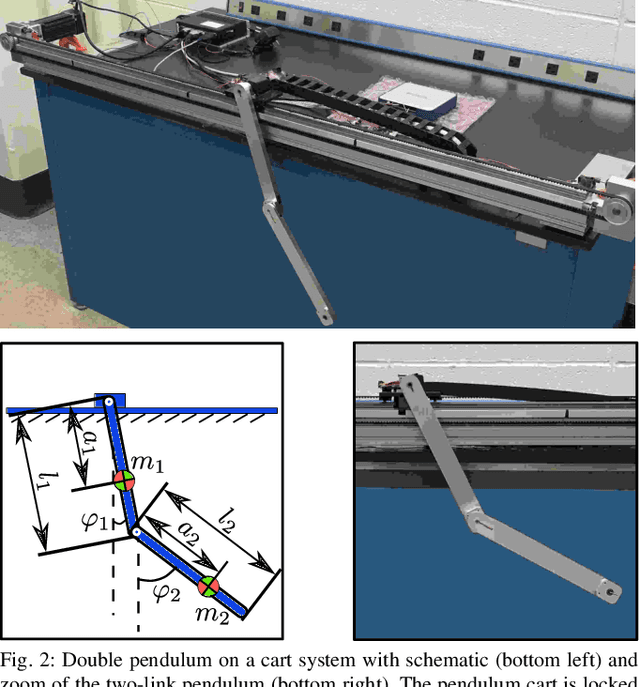
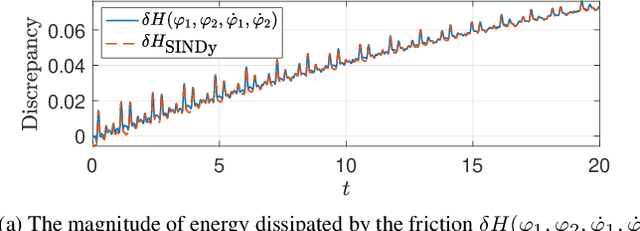
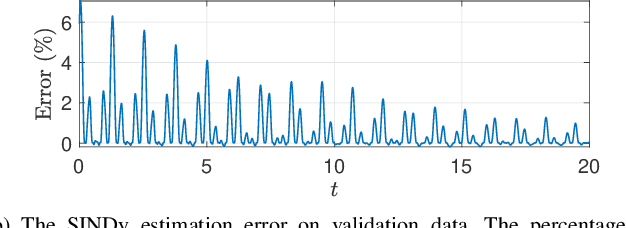
First principles modeling of physical systems has led to significant technological advances across all branches of science. For nonlinear systems, however, small modeling errors can lead to significant deviations from the true, measured behavior. Even in mechanical systems, where the equations are assumed to be well-known, there are often model discrepancies corresponding to nonlinear friction, wind resistance, etc. Discovering models for these discrepancies remains an open challenge for many complex systems. In this work, we use the sparse identification of nonlinear dynamics (SINDy) algorithm to discover a model for the discrepancy between a simplified model and measurement data. In particular, we assume that the model mismatch can be sparsely represented in a library of candidate model terms. We demonstrate the efficacy of our approach on several examples including experimental data from a double pendulum on a cart. We further design and implement a feed-forward controller in simulations, showing improvement with a discrepancy model.

A unified sparse optimization framework to learn parsimonious physics-informed models from data

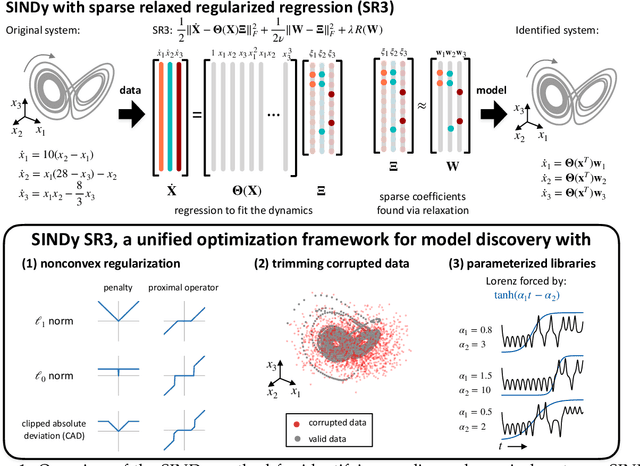
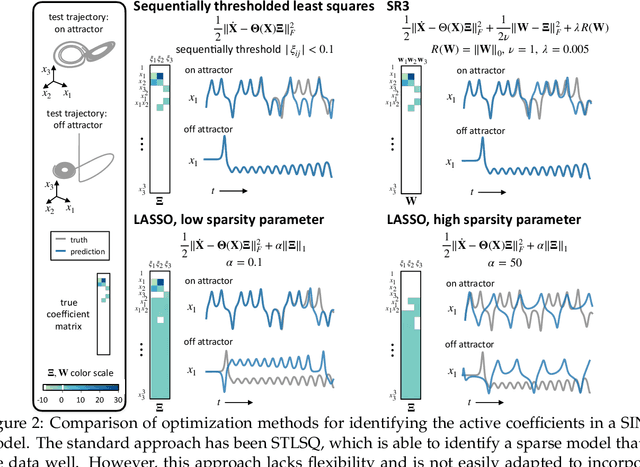
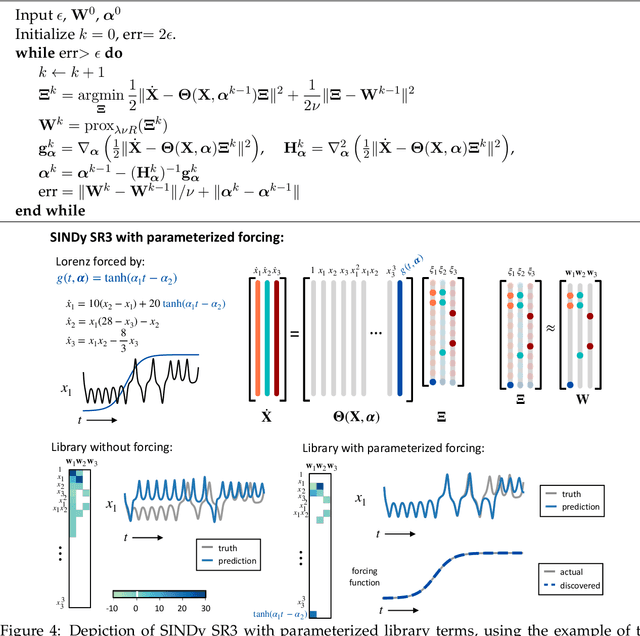
Machine learning (ML) is redefining what is possible in data-intensive fields of science and engineering. However, applying ML to problems in the physical sciences comes with a unique set of challenges: scientists want physically interpretable models that can (i) generalize to predict previously unobserved behaviors, (ii) provide effective forecasting predictions (extrapolation), and (iii) be certifiable. Autonomous systems will necessarily interact with changing and uncertain environments, motivating the need for models that can accurately extrapolate based on physical principles (e.g. Newton's universal second law for classical mechanics, F=ma). Standard ML approaches have shown impressive performance for predicting dynamics in an interpolatory regime, but the resulting models often lack interpretability and fail to generalize. In this paper, we introduce a unified sparse optimization framework that learns governing dynamical systems models from data, selecting relevant terms in the dynamics from a library of possible functions. The resulting models are parsimonious, have physical interpretations, and can generalize to new parameter regimes. Our framework allows the use of non-convex sparsity promoting regularization functions and can be adapted to address key challenges in scientific problems and data sets, including outliers, parametric dependencies, and physical constraints. We show that the approach discovers parsimonious dynamical models on several example systems, including a spiking neuron model. This flexible approach can be tailored to the unique challenges associated with a wide range of applications and data sets, providing a powerful ML-based framework for learning governing models for physical systems from data.