Rescaled Influence Functions: Accurate Data Attribution in High Dimension

How does the training data affect a model's behavior? This is the question we seek to answer with data attribution. The leading practical approaches to data attribution are based on influence functions (IF). IFs utilize a first-order Taylor approximation to efficiently predict the effect of removing a set of samples from the training set without retraining the model, and are used in a wide variety of machine learning applications. However, especially in the high-dimensional regime (# params $\geq \Omega($# samples$)$), they are often imprecise and tend to underestimate the effect of sample removals, even for simple models such as logistic regression. We present rescaled influence functions (RIF), a new tool for data attribution which can be used as a drop-in replacement for influence functions, with little computational overhead but significant improvement in accuracy. We compare IF and RIF on a range of real-world datasets, showing that RIFs offer significantly better predictions in practice, and present a theoretical analysis explaining this improvement. Finally, we present a simple class of data poisoning attacks that would fool IF-based detections but would be detected by RIF.

Robustness Auditing for Linear Regression: To Singularity and Beyond

It has recently been discovered that the conclusions of many highly influential econometrics studies can be overturned by removing a very small fraction of their samples (often less than $0.5\%$). These conclusions are typically based on the results of one or more Ordinary Least Squares (OLS) regressions, raising the question: given a dataset, can we certify the robustness of an OLS fit on this dataset to the removal of a given number of samples? Brute-force techniques quickly break down even on small datasets. Existing approaches which go beyond brute force either can only find candidate small subsets to remove (but cannot certify their non-existence) [BGM20, KZC21], are computationally intractable beyond low dimensional settings [MR22], or require very strong assumptions on the data distribution and too many samples to give reasonable bounds in practice [BP21, FH23]. We present an efficient algorithm for certifying the robustness of linear regressions to removals of samples. We implement our algorithm and run it on several landmark econometrics datasets with hundreds of dimensions and tens of thousands of samples, giving the first non-trivial certificates of robustness to sample removal for datasets of dimension $4$ or greater. We prove that under distributional assumptions on a dataset, the bounds produced by our algorithm are tight up to a $1 + o(1)$ multiplicative factor.

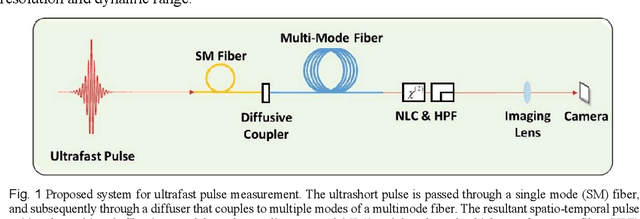
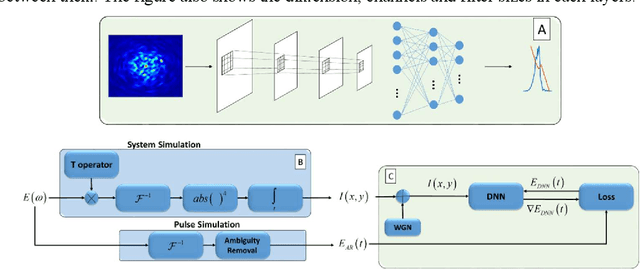
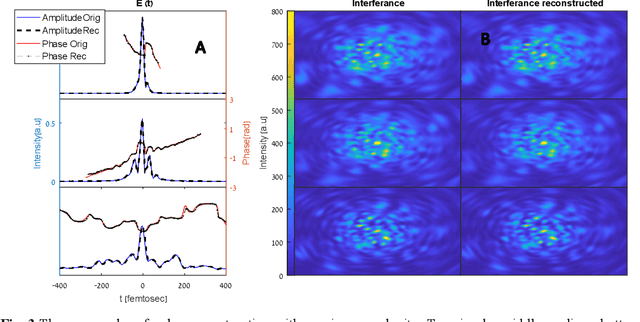
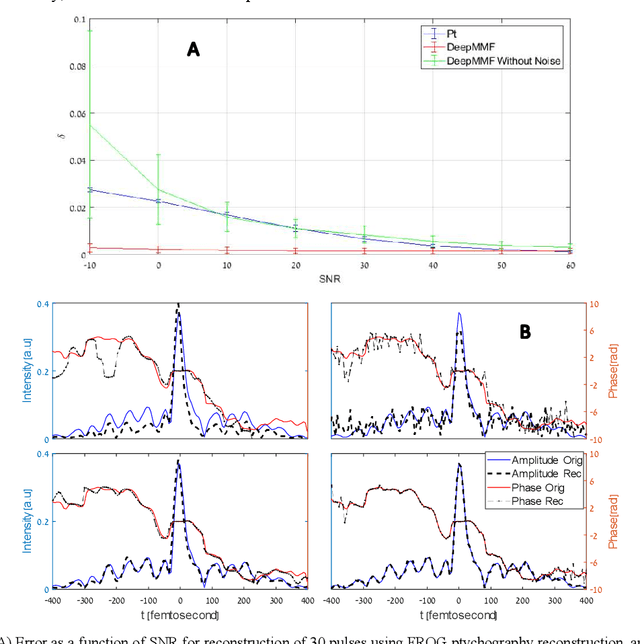
Deep learning reconstruction of ultrashort pulses from 2D spatial intensity patterns recorded by an all-in-line system in a single-shot

We propose a simple all-in-line single-shot scheme for diagnostics of ultrashort laser pulses, consisting of a multi-mode fiber, a nonlinear crystal and a CCD camera. The system records a 2D spatial intensity pattern, from which the pulse shape (amplitude and phase) are recovered, through a fast Deep Learning algorithm. We explore this scheme in simulations and demonstrate the recovery of ultrashort pulses, robustness to noise in measurements and to inaccuracies in the parameters of the system components. Our technique mitigates the need for commonly used iterative optimization reconstruction methods, which are usually slow and hampered by the presence of noise. These features make our concept system advantageous for real time probing of ultrafast processes and noisy conditions. Moreover, this work exemplifies that using deep learning we can unlock new types of systems for pulse recovery.