Ishat E Rabban
Communication-Aware Multi-robot Coordination with Submodular Maximization
Nov 03, 2020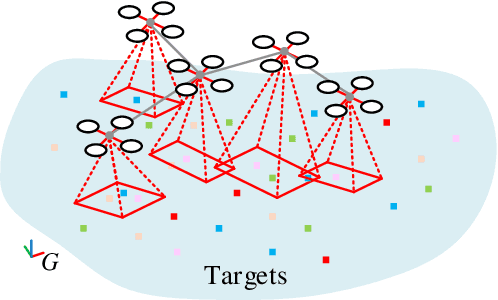
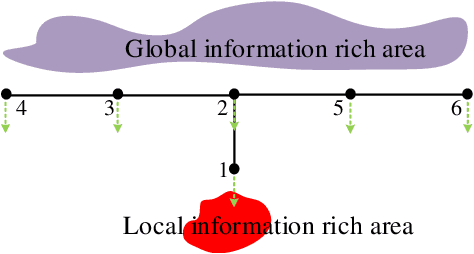
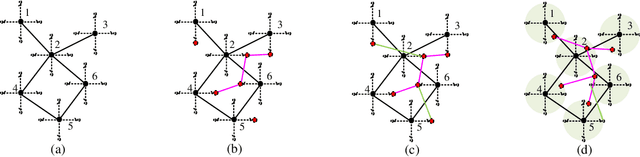
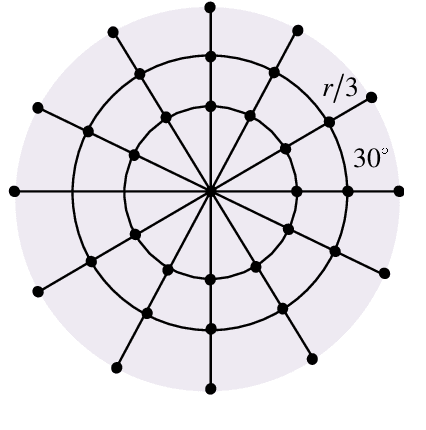
Abstract:Submodular maximization has been widely used in many multi-robot task planning problems including information gathering, exploration, and target tracking. However, the interplay between submodular maximization and communication is rarely explored in the multi-robot setting. In many cases, maximizing the submodular objective may drive the robots in a way so as to disconnect the communication network. Driven by such observations, in this paper, we consider the problem of maximizing submodular function with connectivity constraints. Specifically, we propose a problem called Communication-aware Submodular Maximization (CSM), in which communication maintenance and submodular maximization are jointly considered in the decision-making process. One heuristic algorithm that consists of two stages, i.e. \textit{topology generation} and \textit{deviation minimization} is proposed. We validate the formulation and algorithm through numerical simulation. We find that our algorithm on average suffers only slightly performance decrease compared to the pure greedy strategy.
Fast Biconnectivity Restoration in Multi-Robot Systems for Robust Communication Maintenance
Nov 02, 2020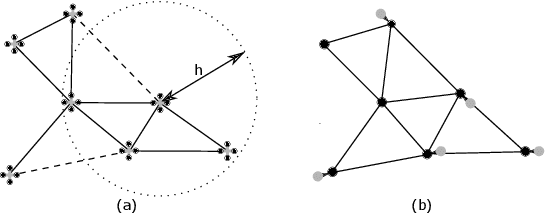
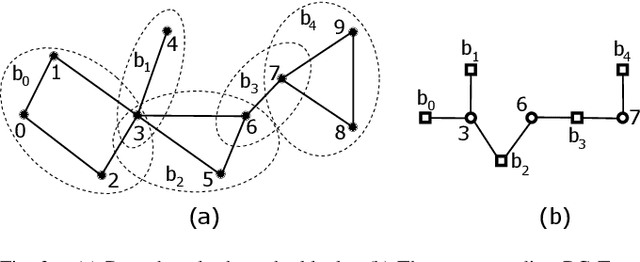
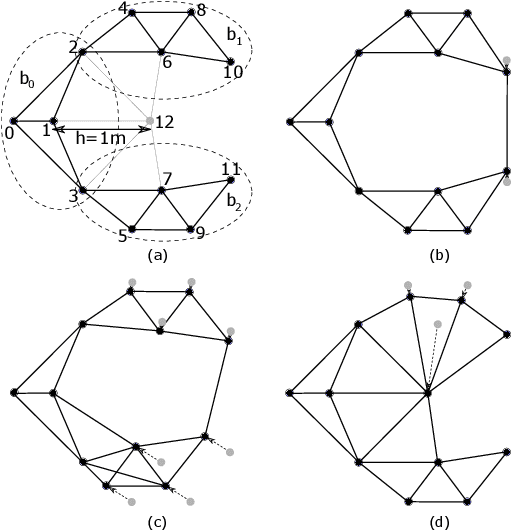
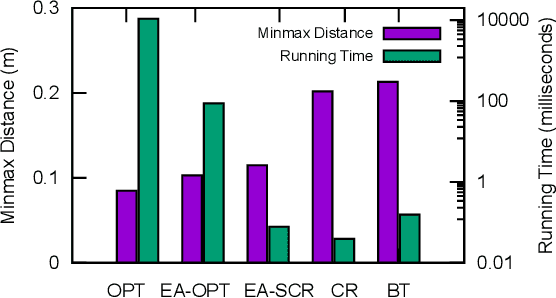
Abstract:Maintaining a robust communication network plays an important role in the success of a multi-robot team jointly performing an optimization task. A key characteristic of a robust multi-robot system is the ability to repair the communication topology itself in the case of robot failure. In this paper, we focus on the Fast Biconnectivity Restoration (FBR) problem, which aims to repair a connected network to make it biconnected as fast as possible, where a biconnected network is a communication topology that cannot be disconnected by removing one node. We develop a Quadratically Constrained Program (QCP) formulation of the FBR problem, which provides a way to optimally solve the problem. We also propose an approximation algorithm for the FBR problem based on graph theory. By conducting empirical studies, we demonstrate that our proposed approximation algorithm performs close to the optimal while significantly outperforming the existing solutions.
Improved Resilient Coverage Maximization with Multiple Robots
Jul 04, 2020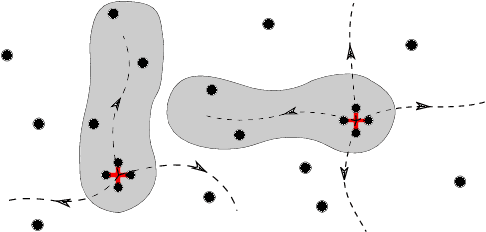
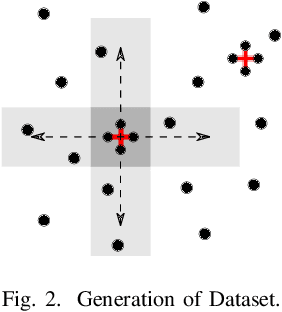
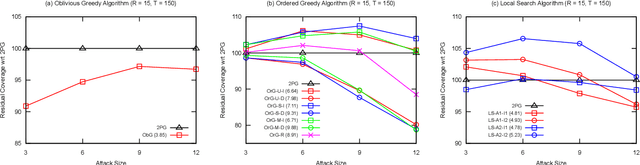
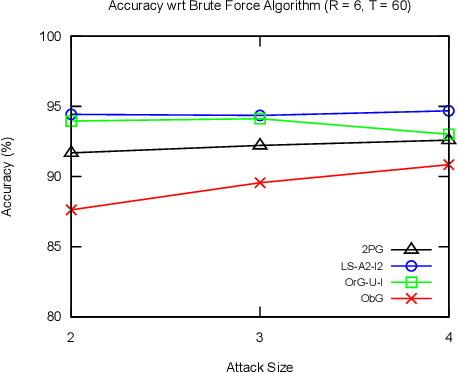
Abstract:The task of maximizing coverage using multiple robots has several applications such as surveillance, exploration, and environmental monitoring. A major challenge of deploying such multi-robot systems in a practical scenario is to ensure resilience against robot failures. A recent work [1] introduced the Resilient Coverage Maximization (RCM) problem where the goal is to maximize a submodular coverage utility when the robots are subject to adversarial attacks and/or failures. The RCM problem is known to be NP-hard. The state-of-the-art solution of the RCM problem [1] employs a greedy approximation strategy with theoretical performance guarantees. In this paper, we propose two approximation algorithms for the RCM problem, both of which empirically outperform the existing solution in terms of accuracy and/or execution time. To demonstrate the effectiveness of our proposed solution, we empirically compare our proposed algorithms with the existing solution and brute force optimum algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge