Active Measure Reinforcement Learning for Observation Cost Minimization

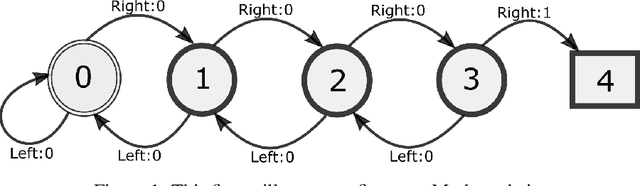
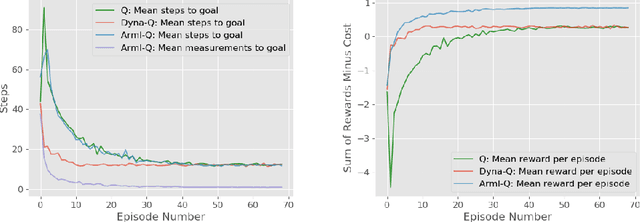
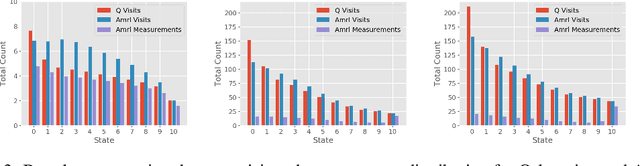
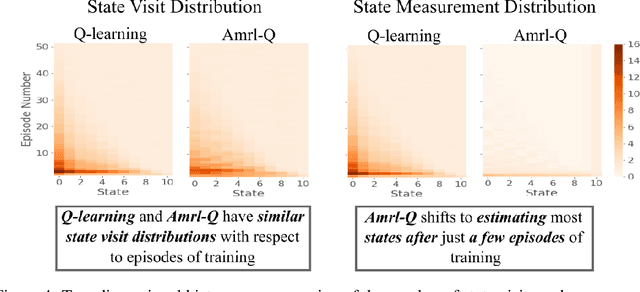
Standard reinforcement learning (RL) algorithms assume that the observation of the next state comes instantaneously and at no cost. In a wide variety of sequential decision making tasks ranging from medical treatment to scientific discovery, however, multiple classes of state observations are possible, each of which has an associated cost. We propose the active measure RL framework (Amrl) as an initial solution to this problem where the agent learns to maximize the costed return, which we define as the discounted sum of rewards minus the sum of observation costs. Our empirical evaluation demonstrates that Amrl-Q agents are able to learn a policy and state estimator in parallel during online training. During training the agent naturally shifts from its reliance on costly measurements of the environment to its state estimator in order to increase its reward. It does this without harm to the learned policy. Our results show that the Amrl-Q agent learns at a rate similar to standard Q-learning and Dyna-Q. Critically, by utilizing an active strategy, Amrl-Q achieves a higher costed return.

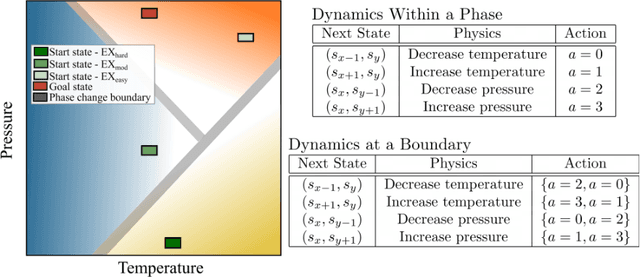
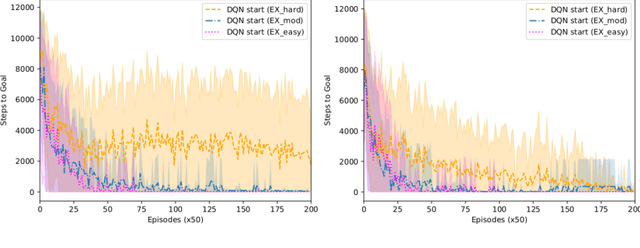
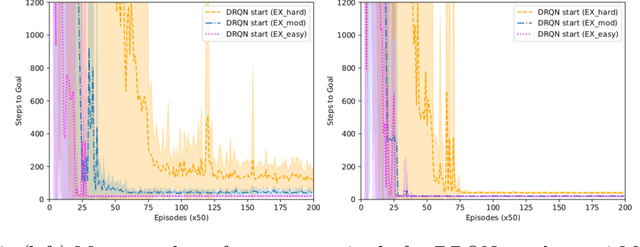
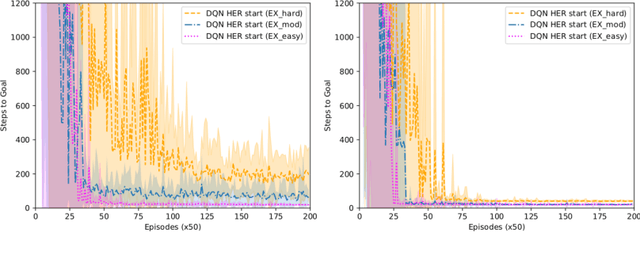
Reinforcement Learning in a Physics-Inspired Semi-Markov Environment

Reinforcement learning (RL) has been demonstrated to have great potential in many applications of scientific discovery and design. Recent work includes, for example, the design of new structures and compositions of molecules for therapeutic drugs. Much of the existing work related to the application of RL to scientific domains, however, assumes that the available state representation obeys the Markov property. For reasons associated with time, cost, sensor accuracy, and gaps in scientific knowledge, many scientific design and discovery problems do not satisfy the Markov property. Thus, something other than a Markov decision process (MDP) should be used to plan / find the optimal policy. In this paper, we present a physics-inspired semi-Markov RL environment, namely the phase change environment. In addition, we evaluate the performance of value-based RL algorithms for both MDPs and partially observable MDPs (POMDPs) on the proposed environment. Our results demonstrate deep recurrent Q-networks (DRQN) significantly outperform deep Q-networks (DQN), and that DRQNs benefit from training with hindsight experience replay. Implications for the use of semi-Markovian RL and POMDPs for scientific laboratories are also discussed.

Watch and learn -- a generalized approach for transferrable learning in deep neural networks via physical principles

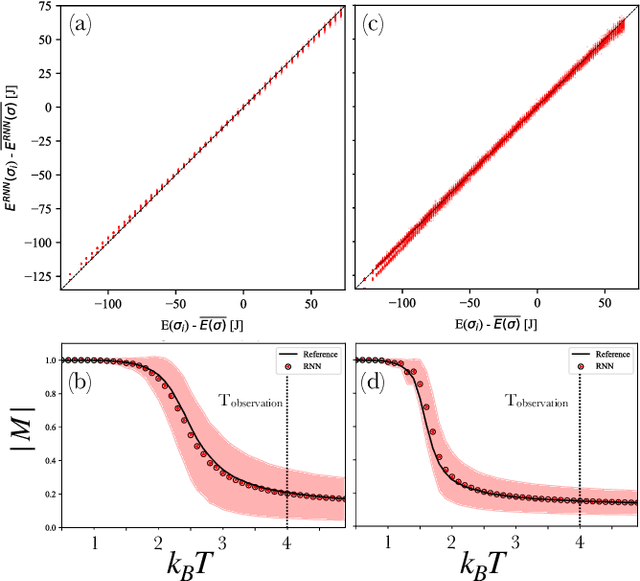
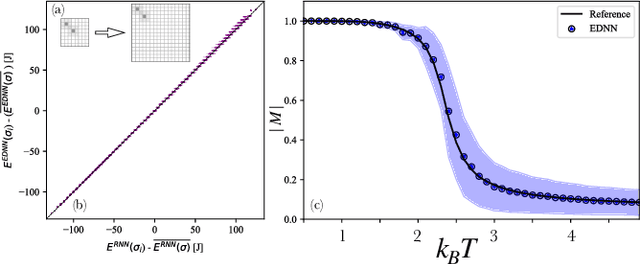
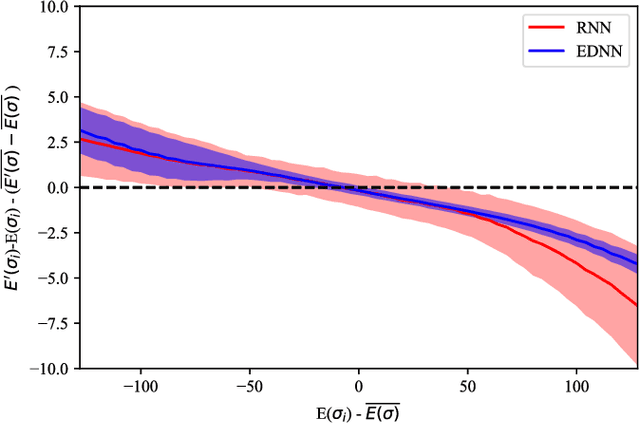
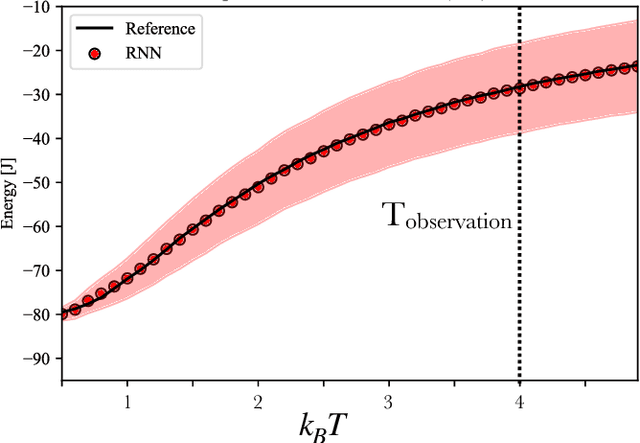
Transfer learning refers to the use of knowledge gained while solving a machine learning task and applying it to the solution of a closely related problem. Such an approach has enabled scientific breakthroughs in computer vision and natural language processing where the weights learned in state-of-the-art models can be used to initialize models for other tasks which dramatically improve their performance and save computational time. Here we demonstrate an unsupervised learning approach augmented with basic physical principles that achieves fully transferrable learning for problems in statistical physics across different physical regimes. By coupling a sequence model based on a recurrent neural network to an extensive deep neural network, we are able to learn the equilibrium probability distributions and inter-particle interaction models of classical statistical mechanical systems. Our approach, distribution-consistent learning, DCL, is a general strategy that works for a variety of canonical statistical mechanical models (Ising and Potts) as well as disordered (spin-glass) interaction potentials. Using data collected from a single set of observation conditions, DCL successfully extrapolates across all temperatures, thermodynamic phases, and can be applied to different length-scales. This constitutes a fully transferrable physics-based learning in a generalizable approach.

Learning to grow: control of materials self-assembly using evolutionary reinforcement learning

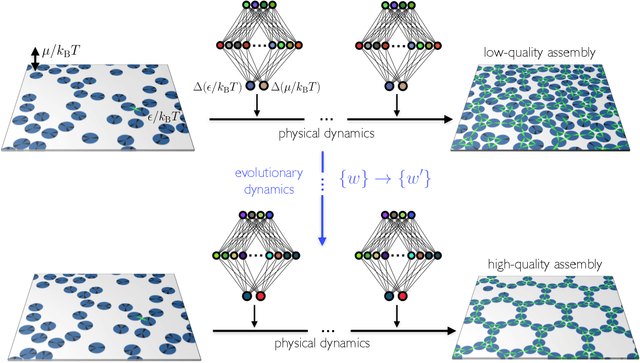
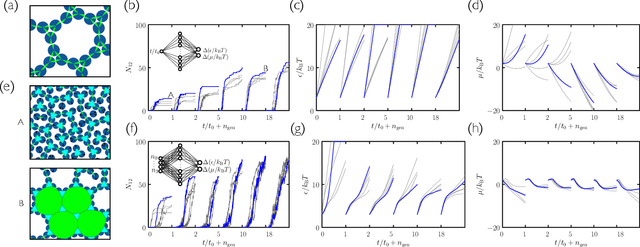
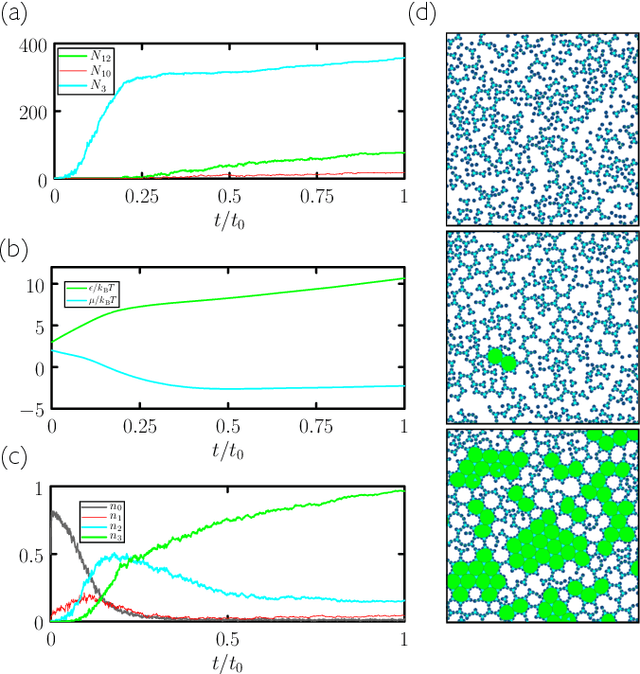
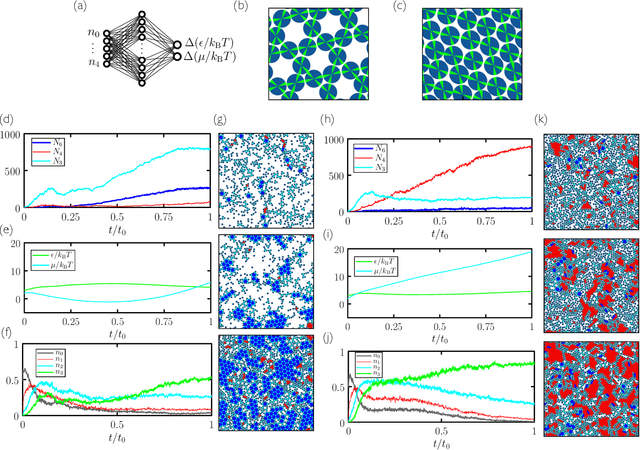
We show that neural networks trained by evolutionary reinforcement learning can enact efficient molecular self-assembly protocols. Presented with molecular simulation trajectories, networks learn to change temperature and chemical potential in order to promote the assembly of desired structures or choose between competing polymorphs. In the first case, networks reproduce in a qualitative sense the results of previously-known protocols, but faster and with higher fidelity; in the second case they identify strategies previously unknown, from which we can extract physical insight. Networks that take as input the elapsed time of the simulation or microscopic information from the system are both effective, the latter more so. The evolutionary scheme we have used is simple to implement and can be applied to a broad range of examples of experimental self-assembly, whether or not one can monitor the experiment as it proceeds. Our results have been achieved with no human input beyond the specification of which order parameter to promote, pointing the way to the design of synthesis protocols by artificial intelligence.

Evolutionary reinforcement learning of dynamical large deviations

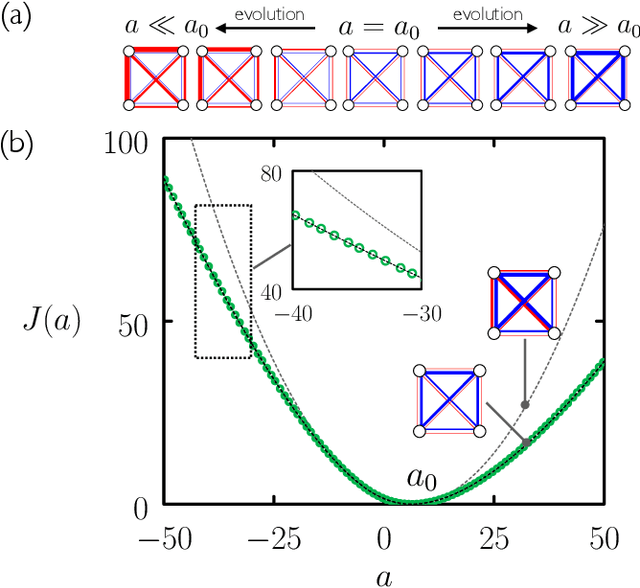
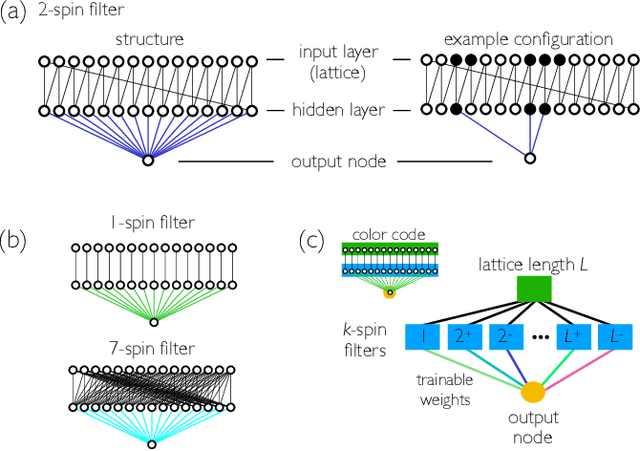
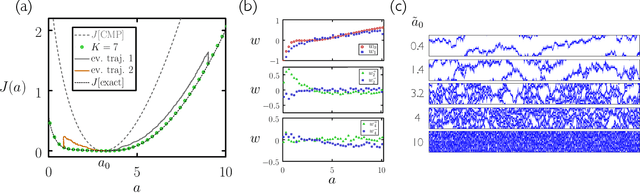
We show how to calculate dynamical large deviations using evolutionary reinforcement learning. An agent, a stochastic model, propagates a continuous-time Monte Carlo trajectory, and receives a reward conditioned upon the values of certain path-extensive quantities. Evolution produces progressively fitter agents, allowing the calculation of a piece of a large-deviation rate function for a particular model and path-extensive quantity. For models with small state spaces the evolutionary process acts directly on rates, and for models with large state spaces the process acts on the weights of a neural network that parameterizes the model's rates. The present approach shows how path-extensive physics problems can be considered within a framework widely used in machine learning.

Optimizing thermodynamic trajectories using evolutionary reinforcement learning

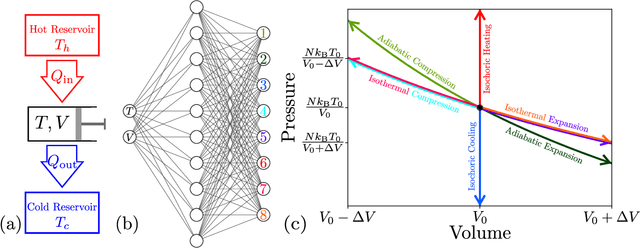
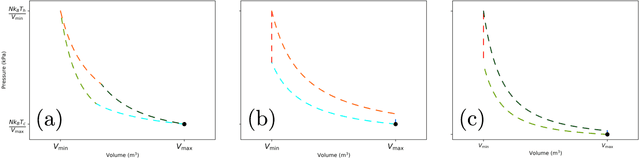
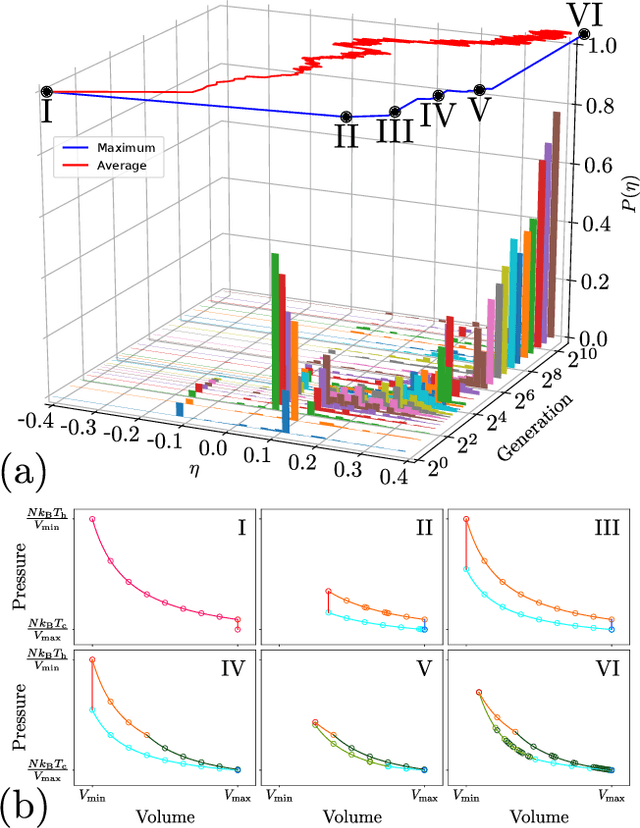
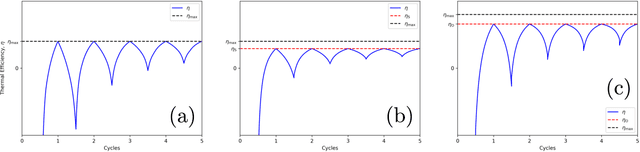
Using a model heat engine we show that neural network-based reinforcement learning can identify thermodynamic trajectories of maximal efficiency. We use an evolutionary learning algorithm to evolve a population of neural networks, subject to a directive to maximize the efficiency of a trajectory composed of a set of elementary thermodynamic processes; the resulting networks learn to carry out the maximally-efficient Carnot, Stirling, or Otto cycles. Given additional irreversible processes this evolutionary scheme learns a hitherto unknown thermodynamic cycle. Our results show how the reinforcement learning strategies developed for game playing can be applied to solve physical problems conditioned upon path-extensive order parameters.

Deep learning and the Schrödinger equation

We have trained a deep (convolutional) neural network to predict the ground-state energy of an electron in four classes of confining two-dimensional electrostatic potentials. On randomly generated potentials, for which there is no analytic form for either the potential or the ground-state energy, the neural network model was able to predict the ground-state energy to within chemical accuracy, with a median absolute error of 1.49 mHa. We also investigate the performance of the model in predicting other quantities such as the kinetic energy and the first excited-state energy of random potentials.