GARLIC: GAussian Representation LearnIng for spaCe partitioning

We introduce GARLIC (GAussian Representation LearnIng for spaCe partitioning), a novel indexing structure based on \(N\)-dimensional Gaussians for efficiently learning high-dimensional vector spaces. Our approach is inspired from Gaussian splatting techniques, typically used in 3D rendering, which we adapt for high-dimensional search and classification. We optimize Gaussian parameters using information-theoretic objectives that balance coverage, assignment confidence, and structural and semantic consistency. A key contribution is to progressively refine the representation through split and clone operations, handling hundreds of dimensions, thus handling varying data densities. GARLIC offers the fast building times of traditional space partitioning methods (e.g., under \(\sim5\) min build time for SIFT1M) while achieving \(\sim50\%\) Recall10@10 in low-candidate regimes. Experimental results on standard benchmarks demonstrate our method's consistency in (a) \(k\)-NN retrieval, outperforming methods, such as Faiss-IVF, in fast-recall by using about half their probes for the same Recall10@10 in Fashion-MNIST, and (b) in classification tasks, beating by \(\sim15\%\) accuracy other majority voting methods. Further, we show strong generalization capabilities, maintaining high accuracy even with downsampled training data: using just \(1\%\) of the training data returns \(\sim 45\%\) Recall@1, thus making GARLIC quite powerful for applications requiring both speed and accuracy.

The assembly modes of rigid 11-bar linkages

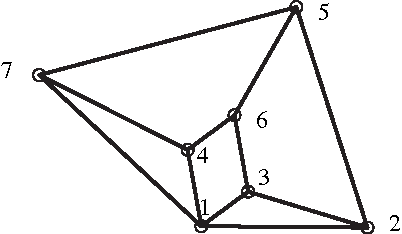
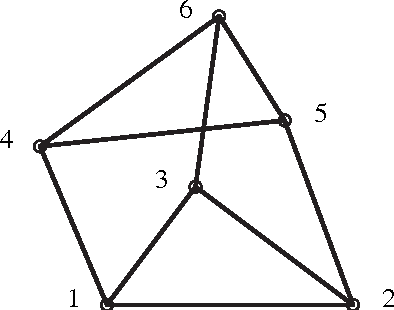
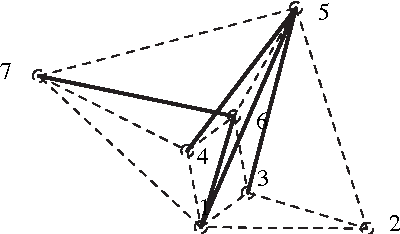
Designing an m-bar linkage with a maximal number of assembly modes is important in robot kinematics, and has further applications in structural biology and computational geometry. A related question concerns the number of assembly modes of rigid mechanisms as a function of their nodes n, which is uniquely defined given m. Rigid 11-bar linkages, where n=7, are the simplest planar linkages for which these questions were still open. It will be proven that the maximal number of assembly modes of such linkages is exactly 56. The rigidity of a linkage is captured by a polynomial system derived from distance, or Cayley-Menger, matrices. The upper bound on the number of assembly modes is obtained as the mixed volume of a 5x5 system. An 11-bar linkage admitting 56 configurations is constructed using stochastic optimisation methods. This yields a general lower bound of $\Omega(2.3^n)$ on the number of assembly modes, slightly improving the current record of $\Omega(2.289^n)$, while the best known upper bound is roughly $4^n$. Our methods are straightforward and have been implemented in Maple. They are described in general terms illustrating the fact that they can be readily extended to other planar or spatial linkages. The main results have been reported in conference publication [EM11]. This version (2017) typesets correctly the last Figure 5 so as to include all 28 configurations modulo reflection.