A Neurosymbolic Framework for Geometric Reduction of Binary Forms

This paper compares Julia reduction and hyperbolic reduction with the aim of finding equivalent binary forms with minimal coefficients. We demonstrate that hyperbolic reduction generally outperforms Julia reduction, particularly in the cases of sextics and decimics, though neither method guarantees achieving the minimal form. We further propose an additional shift and scaling to approximate the minimal form more closely. Finally, we introduce a machine learning framework to identify optimal transformations that minimize the heights of binary forms. This study provides new insights into the geometry and algebra of binary forms and highlights the potential of AI in advancing symbolic computation and reduction techniques. The findings, supported by extensive computational experiments, lay the groundwork for hybrid approaches that integrate traditional reduction methods with data-driven techniques.

A SAT-based Resolution of Lam's Problem

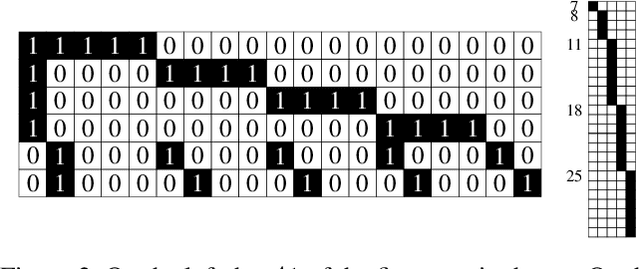
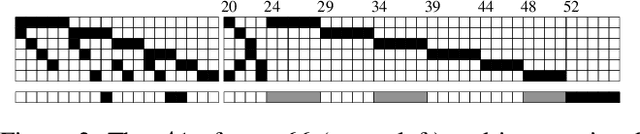
In 1989, computer searches by Lam, Thiel, and Swiercz experimentally resolved Lam's problem from projective geometry$\unicode{x2014}$the long-standing problem of determining if a projective plane of order ten exists. Both the original search and an independent verification in 2011 discovered no such projective plane. However, these searches were each performed using highly specialized custom-written code and did not produce nonexistence certificates. In this paper, we resolve Lam's problem by translating the problem into Boolean logic and use satisfiability (SAT) solvers to produce nonexistence certificates that can be verified by a third party. Our work uncovered consistency issues in both previous searches$\unicode{x2014}$highlighting the difficulty of relying on special-purpose search code for nonexistence results.

Effective problem solving using SAT solvers

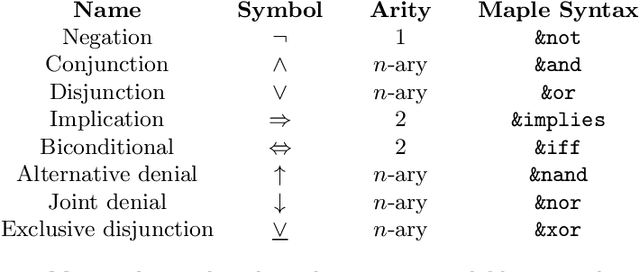
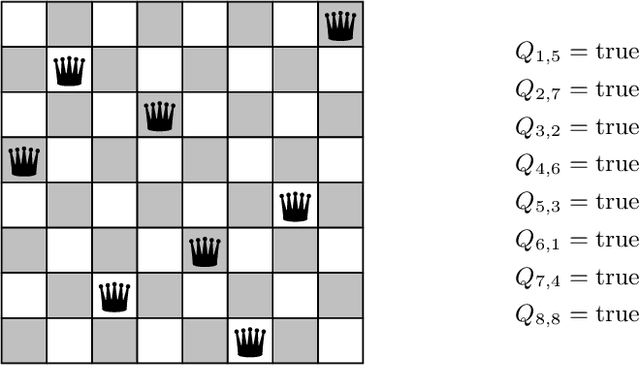
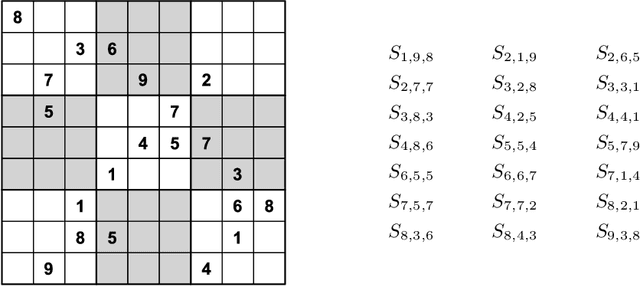
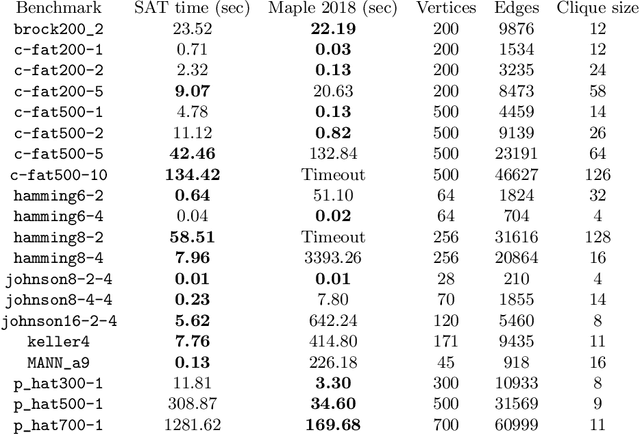
In this article we demonstrate how to solve a variety of problems and puzzles using the built-in SAT solver of the computer algebra system Maple. Once the problems have been encoded into Boolean logic, solutions can be found (or shown to not exist) automatically, without the need to implement any search algorithm. In particular, we describe how to solve the $n$-queens problem, how to generate and solve Sudoku puzzles, how to solve logic puzzles like the Einstein riddle, how to solve the 15-puzzle, how to solve the maximum clique problem, and finding Graeco-Latin squares.