Exact Statistical Inference for Time Series Similarity using Dynamic Time Warping by Selective Inference

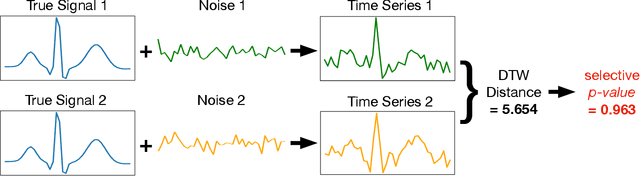
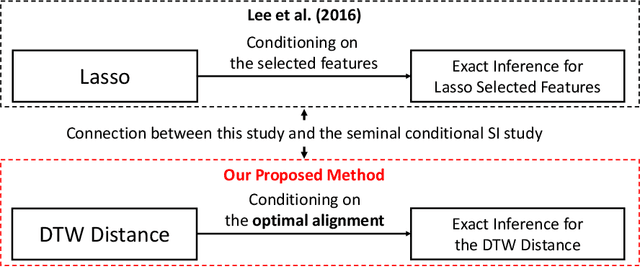
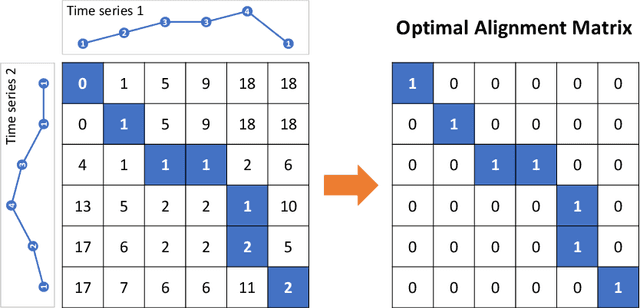
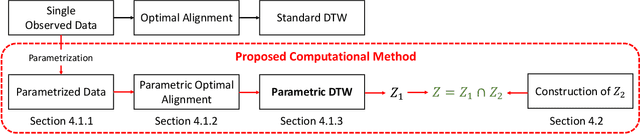
In this paper, we study statistical inference on the similarity/distance between two time-series under uncertain environment by considering a statistical hypothesis test on the distance obtained from Dynamic Time Warping (DTW) algorithm. The sampling distribution of the DTW distance is too complicated to derive because it is obtained based on the solution of a complicated algorithm. To circumvent this difficulty, we propose to employ a conditional sampling distribution for the inference, which enables us to derive an exact (non-asymptotic) inference method on the DTW distance. Besides, we also develop a novel computational method to compute the conditional sampling distribution. To our knowledge, this is the first method that can provide valid $p$-value to quantify the statistical significance of the DTW distance, which is helpful for high-stake decision making. We evaluate the performance of the proposed inference method on both synthetic and real-world datasets.

Bayesian Optimization for Distributionally Robust Chance-constrained Problem

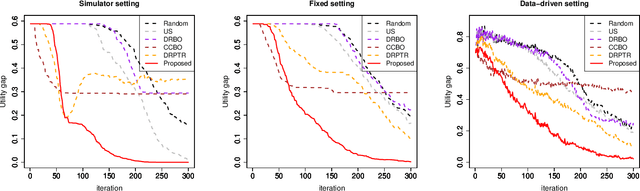
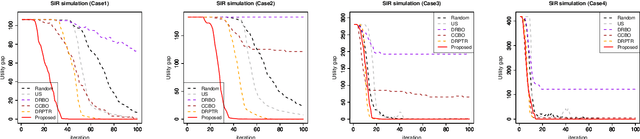
In black-box function optimization, we need to consider not only controllable design variables but also uncontrollable stochastic environment variables. In such cases, it is necessary to solve the optimization problem by taking into account the uncertainty of the environmental variables. Chance-constrained (CC) problem, the problem of maximizing the expected value under a certain level of constraint satisfaction probability, is one of the practically important problems in the presence of environmental variables. In this study, we consider distributionally robust CC (DRCC) problem and propose a novel DRCC Bayesian optimization method for the case where the distribution of the environmental variables cannot be precisely specified. We show that the proposed method can find an arbitrary accurate solution with high probability in a finite number of trials, and confirm the usefulness of the proposed method through numerical experiments.

Continuation Path with Linear Convergence Rate

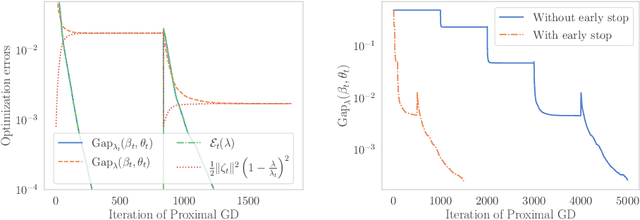
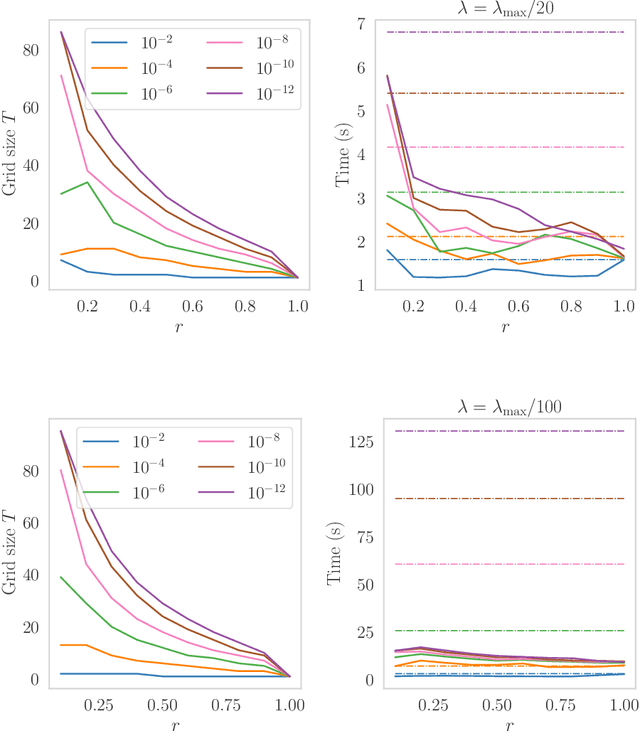
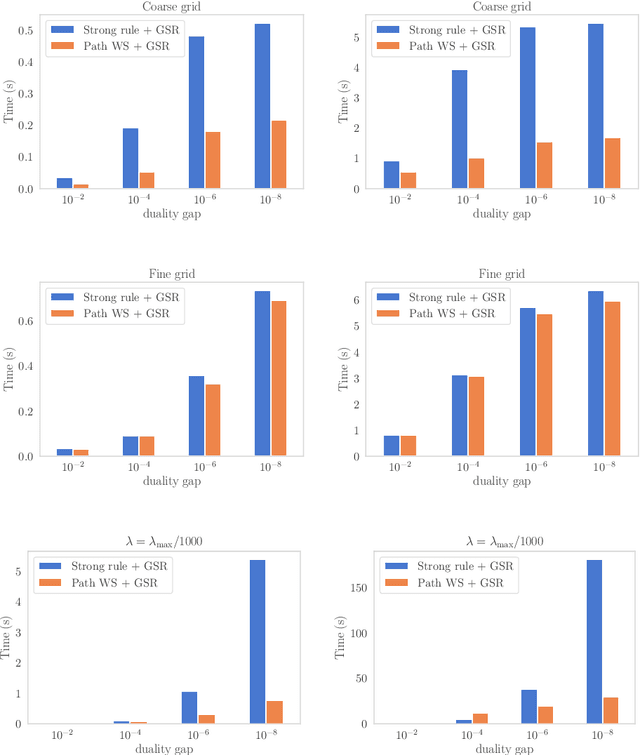
Path-following algorithms are frequently used in composite optimization problems where a series of subproblems, with varying regularization hyperparameters, are solved sequentially. By reusing the previous solutions as initialization, better convergence speeds have been observed numerically. This makes it a rather useful heuristic to speed up the execution of optimization algorithms in machine learning. We present a primal dual analysis of the path-following algorithm and explore how to design its hyperparameters as well as determining how accurately each subproblem should be solved to guarantee a linear convergence rate on a target problem. Furthermore, considering optimization with a sparsity-inducing penalty, we analyze the change of the active sets with respect to the regularization parameter. The latter can then be adaptively calibrated to finely determine the number of features that will be selected along the solution path. This leads to simple heuristics for calibrating hyperparameters of active set approaches to reduce their complexity and improve their execution time.

Topic Analysis of Superconductivity Literature by Semantic Non-negative Matrix Factorization

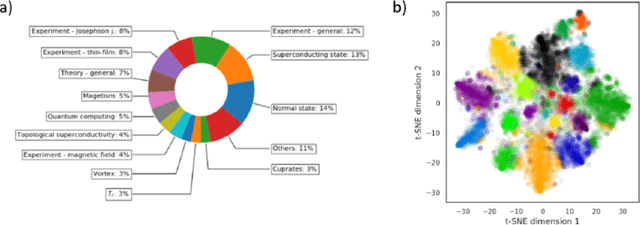
We utilize a recently developed topic modeling method called SeNMFk, extending the standard Non-negative Matrix Factorization (NMF) methods by incorporating the semantic structure of the text, and adding a robust system for determining the number of topics. With SeNMFk, we were able to extract coherent topics validated by human experts. From these topics, a few are relatively general and cover broad concepts, while the majority can be precisely mapped to specific scientific effects or measurement techniques. The topics also differ by ubiquity, with only three topics prevalent in almost 40 percent of the abstract, while each specific topic tends to dominate a small subset of the abstracts. These results demonstrate the ability of SeNMFk to produce a layered and nuanced analysis of large scientific corpora.

Bayesian Optimization for Cascade-type Multi-stage Processes

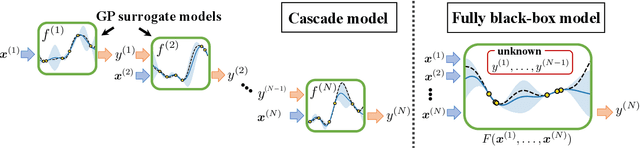
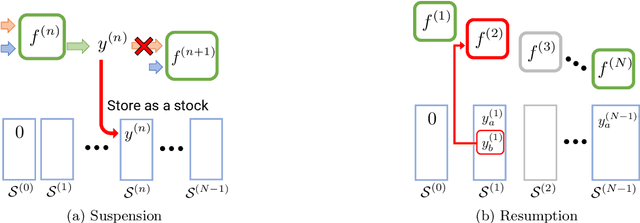
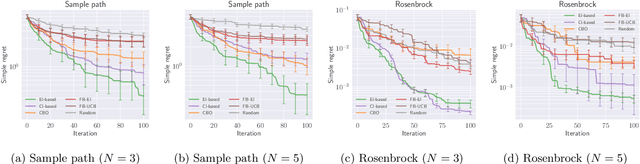
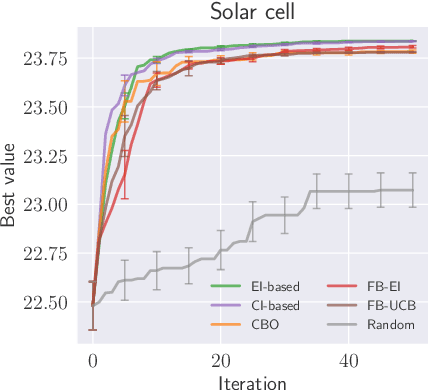
Complex processes in science and engineering are often formulated as multi-stage decision-making problems. In this paper, we consider a type of multi-stage decision-making process called a cascade process. A cascade process is a multi-stage process in which the output of one stage is used as an input for the next stage. When the cost of each stage is expensive, it is difficult to search for the optimal controllable parameters for each stage exhaustively. To address this problem, we formulate the optimization of the cascade process as an extension of Bayesian optimization framework and propose two types of acquisition functions (AFs) based on credible intervals and expected improvement. We investigate the theoretical properties of the proposed AFs and demonstrate their effectiveness through numerical experiments. In addition, we consider an extension called suspension setting in which we are allowed to suspend the cascade process at the middle of the multi-stage decision-making process that often arises in practical problems. We apply the proposed method in the optimization problem of the solar cell simulator, which was the motivation for this study.

Physics in the Machine: Integrating Physical Knowledge in Autonomous Phase-Mapping

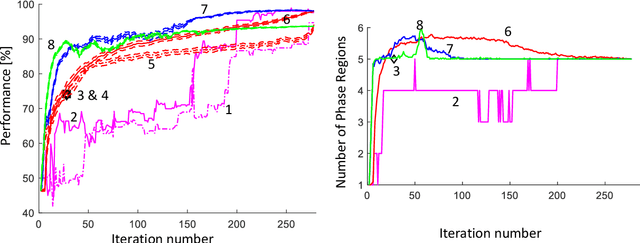
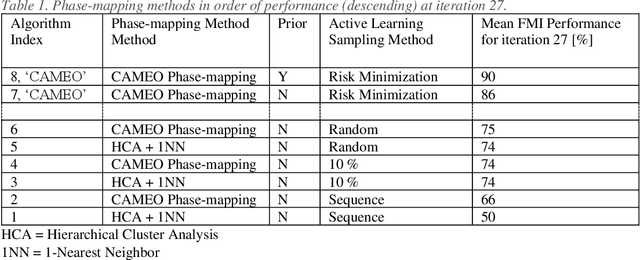
Application of artificial intelligence (AI), and more specifically machine learning, to the physical sciences has expanded significantly over the past decades. In particular, science-informed AI or scientific AI has grown from a focus on data analysis to now controlling experiment design, simulation, execution and analysis in closed-loop autonomous systems. The CAMEO (closed-loop autonomous materials exploration and optimization) algorithm employs scientific AI to address two tasks: learning a material system's composition-structure relationship and identifying materials compositions with optimal functional properties. By integrating these, accelerated materials screening across compositional phase diagrams was demonstrated, resulting in the discovery of a best-in-class phase change memory material. Key to this success is the ability to guide subsequent measurements to maximize knowledge of the composition-structure relationship, or phase map. In this work we investigate the benefits of incorporating varying levels of prior physical knowledge into CAMEO's autonomous phase-mapping. This includes the use of ab-initio phase boundary data from the AFLOW repositories, which has been shown to optimize CAMEO's search when used as a prior.

Valid and Exact Statistical Inference for Multi-dimensional Multiple Change-Points by Selective Inference

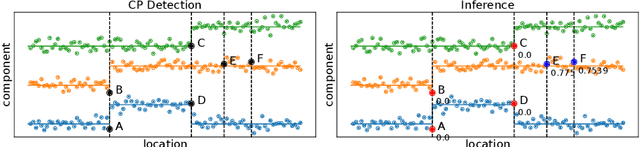
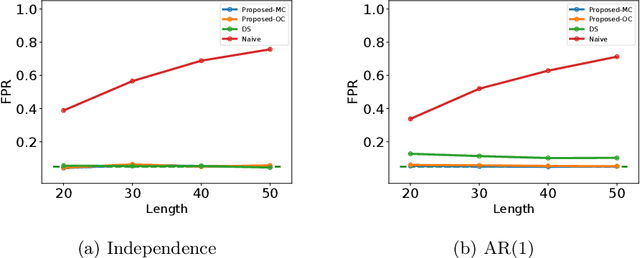
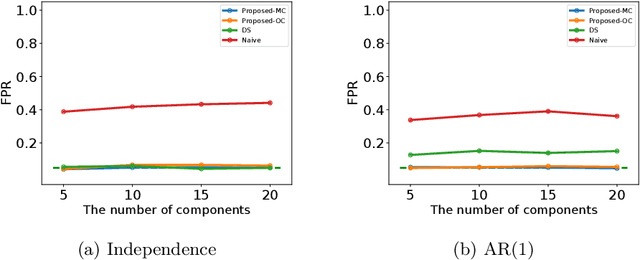
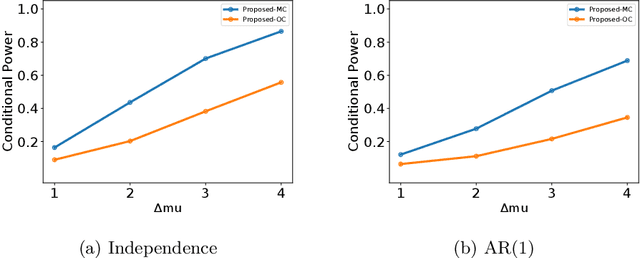
In this paper, we study statistical inference of change-points (CPs) in multi-dimensional sequence. In CP detection from a multi-dimensional sequence, it is often desirable not only to detect the location, but also to identify the subset of the components in which the change occurs. Several algorithms have been proposed for such problems, but no valid exact inference method has been established to evaluate the statistical reliability of the detected locations and components. In this study, we propose a method that can guarantee the statistical reliability of both the location and the components of the detected changes. We demonstrate the effectiveness of the proposed method by applying it to the problems of genomic abnormality identification and human behavior analysis.

Exact Statistical Inference for the Wasserstein Distance by Selective Inference

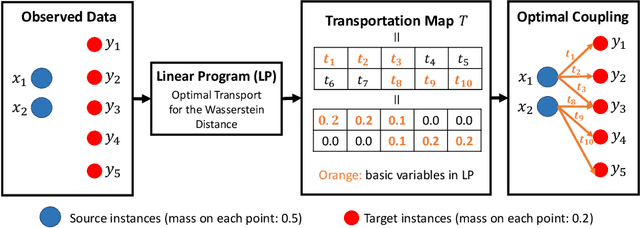
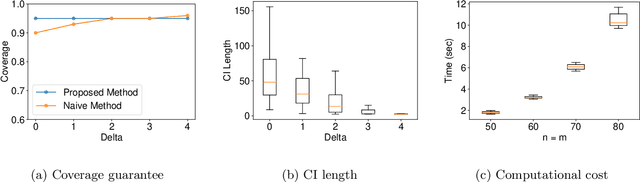
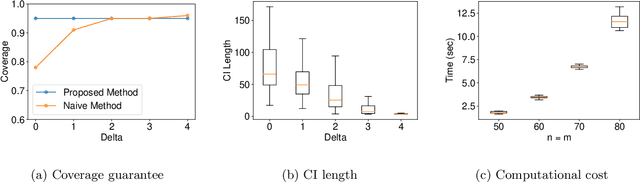
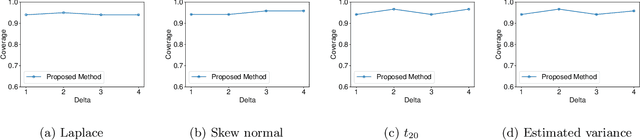
In this paper, we study statistical inference for the Wasserstein distance, which has attracted much attention and has been applied to various machine learning tasks. Several studies have been proposed in the literature, but almost all of them are based on asymptotic approximation and do not have finite-sample validity. In this study, we propose an exact (non-asymptotic) inference method for the Wasserstein distance inspired by the concept of conditional Selective Inference (SI). To our knowledge, this is the first method that can provide a valid confidence interval (CI) for the Wasserstein distance with finite-sample coverage guarantee, which can be applied not only to one-dimensional problems but also to multi-dimensional problems. We evaluate the performance of the proposed method on both synthetic and real-world datasets.

Case-based similar image retrieval for weakly annotated large histopathological images of malignant lymphoma using deep metric learning

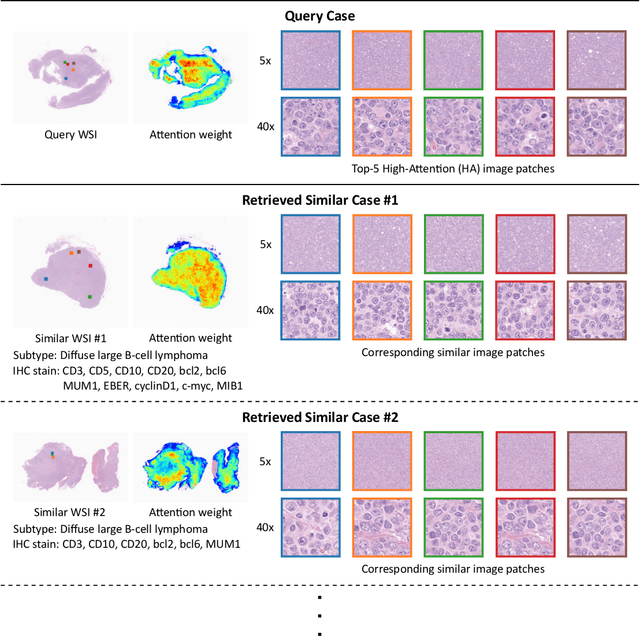
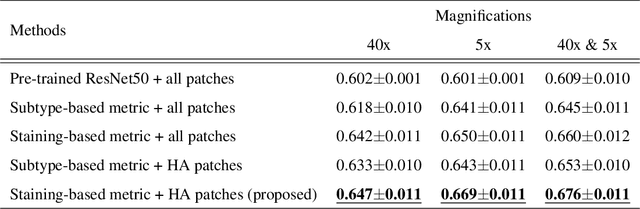
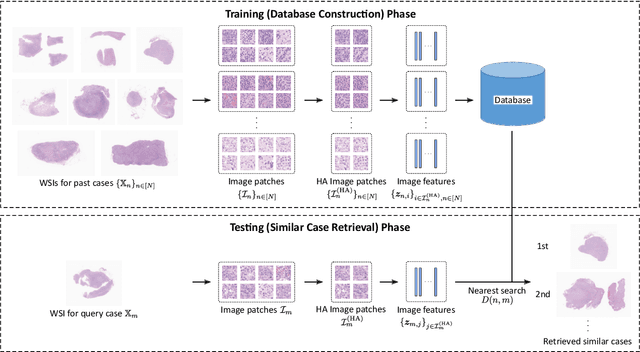
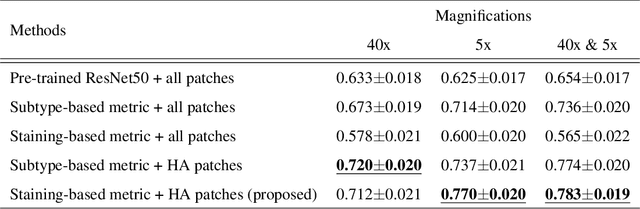
In the present study, we propose a novel case-based similar image retrieval (SIR) method for hematoxylin and eosin (H&E)-stained histopathological images of malignant lymphoma. When a whole slide image (WSI) is used as an input query, it is desirable to be able to retrieve similar cases by focusing on image patches in pathologically important regions such as tumor cells. To address this problem, we employ attention-based multiple instance learning, which enables us to focus on tumor-specific regions when the similarity between cases is computed. Moreover, we employ contrastive distance metric learning to incorporate immunohistochemical (IHC) staining patterns as useful supervised information for defining appropriate similarity between heterogeneous malignant lymphoma cases. In the experiment with 249 malignant lymphoma patients, we confirmed that the proposed method exhibited higher evaluation measures than the baseline case-based SIR methods. Furthermore, the subjective evaluation by pathologists revealed that our similarity measure using IHC staining patterns is appropriate for representing the similarity of H&E-stained tissue images for malignant lymphoma.

Fast and More Powerful Selective Inference for Sparse High-order Interaction Model

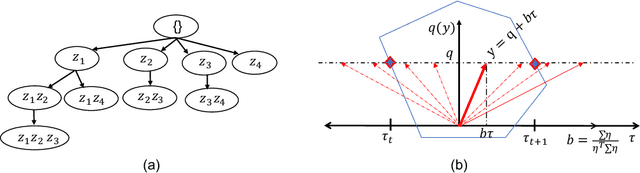
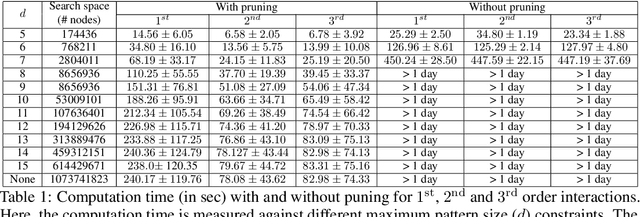
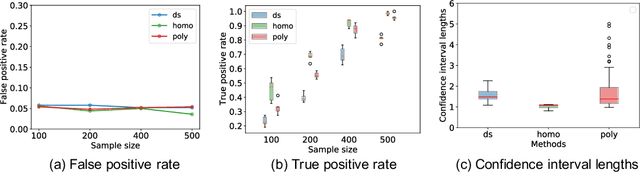
Automated high-stake decision-making such as medical diagnosis requires models with high interpretability and reliability. As one of the interpretable and reliable models with good prediction ability, we consider Sparse High-order Interaction Model (SHIM) in this study. However, finding statistically significant high-order interactions is challenging due to the intrinsic high dimensionality of the combinatorial effects. Another problem in data-driven modeling is the effect of "cherry-picking" a.k.a. selection bias. Our main contribution is to extend the recently developed parametric programming approach for selective inference to high-order interaction models. Exhaustive search over the cherry tree (all possible interactions) can be daunting and impractical even for a small-sized problem. We introduced an efficient pruning strategy and demonstrated the computational efficiency and statistical power of the proposed method using both synthetic and real data.