Continuation Path with Linear Convergence Rate
Paper and Code
Dec 09, 2021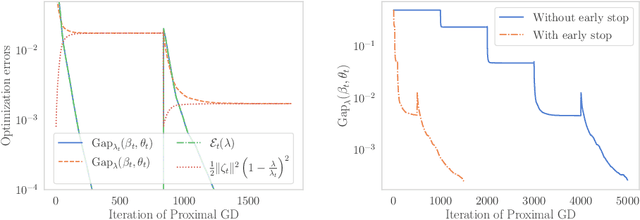
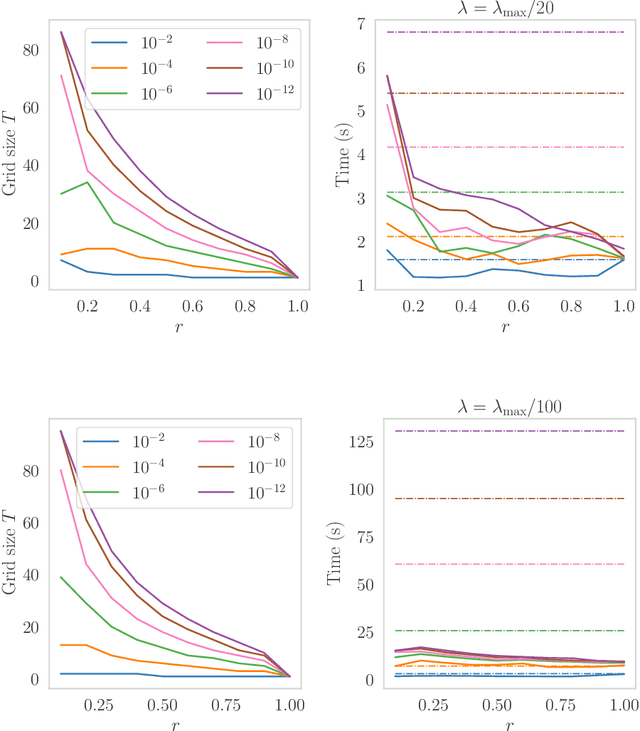
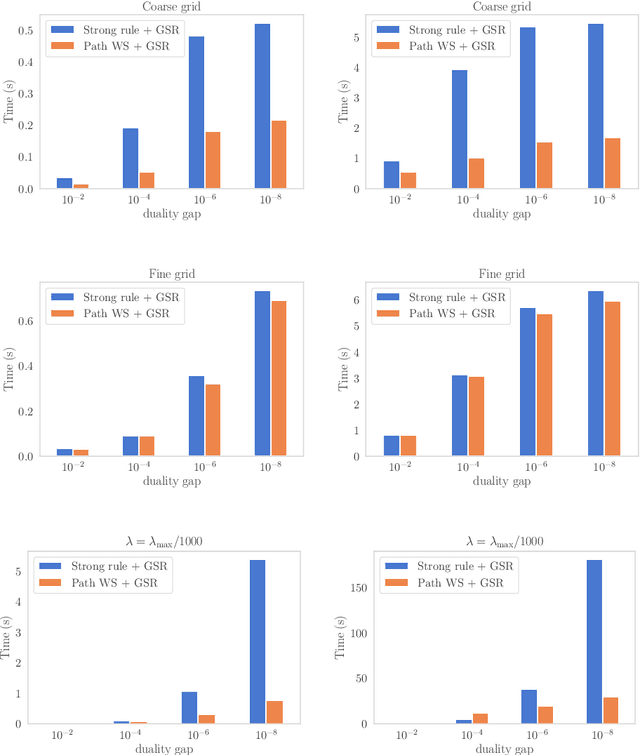
Path-following algorithms are frequently used in composite optimization problems where a series of subproblems, with varying regularization hyperparameters, are solved sequentially. By reusing the previous solutions as initialization, better convergence speeds have been observed numerically. This makes it a rather useful heuristic to speed up the execution of optimization algorithms in machine learning. We present a primal dual analysis of the path-following algorithm and explore how to design its hyperparameters as well as determining how accurately each subproblem should be solved to guarantee a linear convergence rate on a target problem. Furthermore, considering optimization with a sparsity-inducing penalty, we analyze the change of the active sets with respect to the regularization parameter. The latter can then be adaptively calibrated to finely determine the number of features that will be selected along the solution path. This leads to simple heuristics for calibrating hyperparameters of active set approaches to reduce their complexity and improve their execution time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge