SCOPE: Spectral Concentration by Distributionally Robust Joint Covariance-Precision Estimation

We propose a distributionally robust formulation for simultaneously estimating the covariance matrix and the precision matrix of a random vector.The proposed model minimizes the worst-case weighted sum of the Frobenius loss of the covariance estimator and Stein's loss of the precision matrix estimator against all distributions from an ambiguity set centered at the nominal distribution. The radius of the ambiguity set is measured via convex spectral divergence. We demonstrate that the proposed distributionally robust estimation model can be reduced to a convex optimization problem, thereby yielding quasi-analytical estimators. The joint estimators are shown to be nonlinear shrinkage estimators. The eigenvalues of the estimators are shrunk nonlinearly towards a positive scalar, where the scalar is determined by the weight coefficient of the loss terms. By tuning the coefficient carefully, the shrinkage corrects the spectral bias of the empirical covariance/precision matrix estimator. By this property, we call the proposed joint estimator the Spectral concentrated COvariance and Precision matrix Estimator (SCOPE). We demonstrate that the shrinkage effect improves the condition number of the estimator. We provide a parameter-tuning scheme that adjusts the shrinkage target and intensity that is asymptotically optimal. Numerical experiments on synthetic and real data show that our shrinkage estimators perform competitively against state-of-the-art estimators in practical applications.

Preference Elicitation and Robust Optimization with Multi-Attribute Quasi-Concave Choice Functions

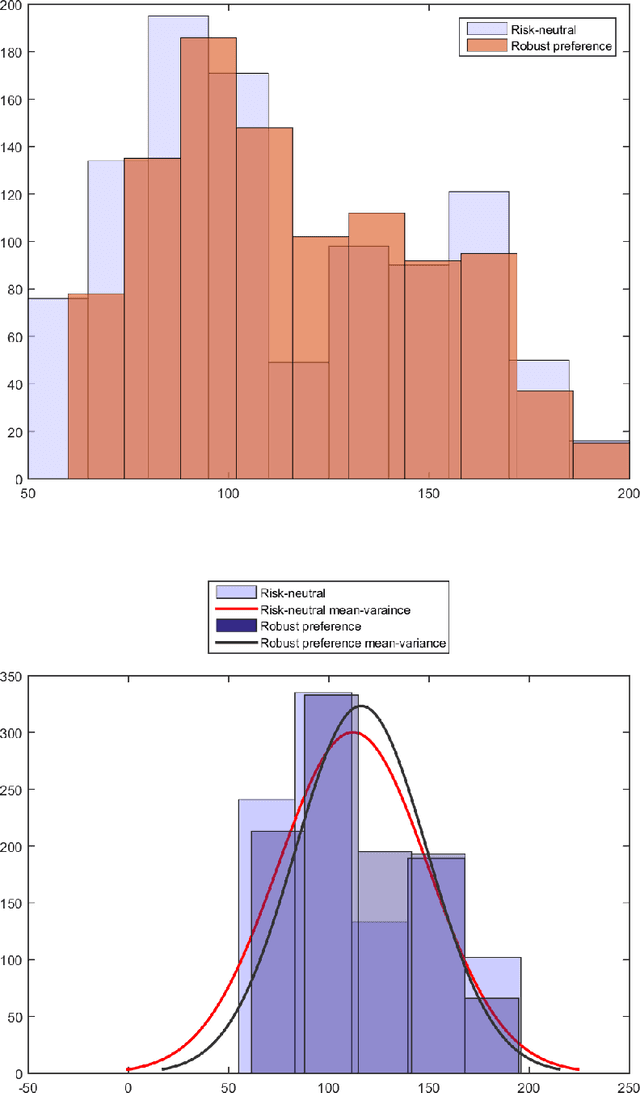
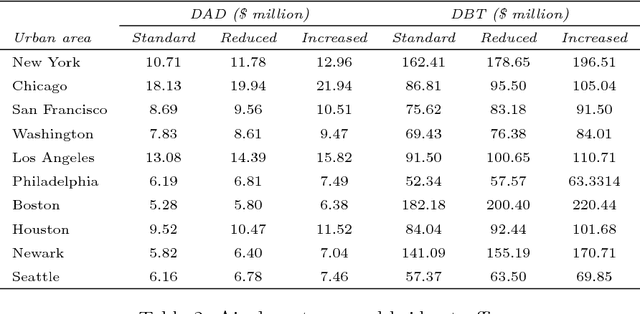
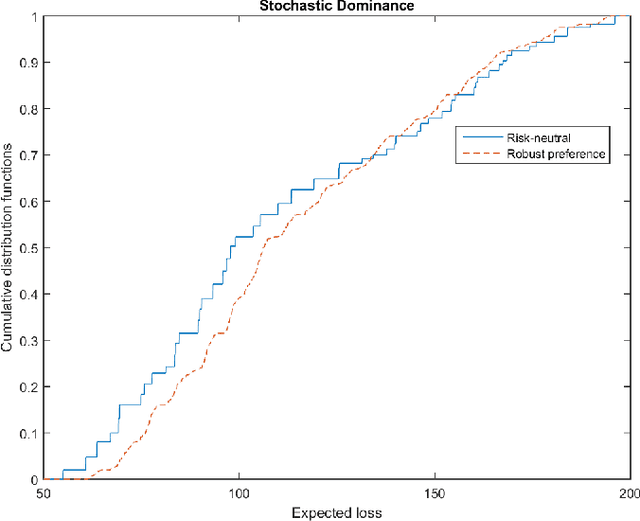
Decision maker's preferences are often captured by some choice functions which are used to rank prospects. In this paper, we consider ambiguity in choice functions over a multi-attribute prospect space. Our main result is a robust preference model where the optimal decision is based on the worst-case choice function from an ambiguity set constructed through preference elicitation with pairwise comparisons of prospects. Differing from existing works in the area, our focus is on quasi-concave choice functions rather than concave functions and this enables us to cover a wide range of utility/risk preference problems including multi-attribute expected utility and $S$-shaped aspirational risk preferences. The robust choice function is increasing and quasi-concave but not necessarily translation invariant, a key property of monetary risk measures. We propose two approaches based respectively on the support functions and level functions of quasi-concave functions to develop tractable formulations of the maximin preference robust optimization model. The former gives rise to a mixed integer linear programming problem whereas the latter is equivalent to solving a sequence of convex risk minimization problems. To assess the effectiveness of the proposed robust preference optimization model and numerical schemes, we apply them to a security budget allocation problem and report some preliminary results from experiments.