Forecasting Geopolitical Events with a Sparse Temporal Fusion Transformer and Gaussian Process Hybrid: A Case Study in Middle Eastern and U.S. Conflict Dynamics

Forecasting geopolitical conflict from data sources like the Global Database of Events, Language, and Tone (GDELT) is a critical challenge for national security. The inherent sparsity, burstiness, and overdispersion of such data cause standard deep learning models, including the Temporal Fusion Transformer (TFT), to produce unreliable long-horizon predictions. We introduce STFT-VNNGP, a hybrid architecture that won the 2023 Algorithms for Threat Detection (ATD) competition by overcoming these limitations. Designed to bridge this gap, our model employs a two-stage process: first, a TFT captures complex temporal dynamics to generate multi-quantile forecasts. These quantiles then serve as informed inputs for a Variational Nearest Neighbor Gaussian Process (VNNGP), which performs principled spatiotemporal smoothing and uncertainty quantification. In a case study forecasting conflict dynamics in the Middle East and the U.S., STFT-VNNGP consistently outperforms a standalone TFT, showing a superior ability to predict the timing and magnitude of bursty event periods, particularly at long-range horizons. This work offers a robust framework for generating more reliable and actionable intelligence from challenging event data, with all code and workflows made publicly available to ensure reproducibility.

Artificial Intelligence for Personalized Prediction of Alzheimer's Disease Progression: A Survey of Methods, Data Challenges, and Future Directions

Alzheimer's Disease (AD) is marked by significant inter-individual variability in its progression, complicating accurate prognosis and personalized care planning. This heterogeneity underscores the critical need for predictive models capable of forecasting patient-specific disease trajectories. Artificial Intelligence (AI) offers powerful tools to address this challenge by analyzing complex, multi-modal, and longitudinal patient data. This paper provides a comprehensive survey of AI methodologies applied to personalized AD progression prediction. We review key approaches including state-space models for capturing temporal dynamics, deep learning techniques like Recurrent Neural Networks for sequence modeling, Graph Neural Networks (GNNs) for leveraging network structures, and the emerging concept of AI-driven digital twins for individualized simulation. Recognizing that data limitations often impede progress, we examine common challenges such as high dimensionality, missing data, and dataset imbalance. We further discuss AI-driven mitigation strategies, with a specific focus on synthetic data generation using Variational Autoencoders (VAEs) and Generative Adversarial Networks (GANs) to augment and balance datasets. The survey synthesizes the strengths and limitations of current approaches, emphasizing the trend towards multimodal integration and the persistent need for model interpretability and generalizability. Finally, we identify critical open challenges, including robust external validation, clinical integration, and ethical considerations, and outline promising future research directions such as hybrid models, causal inference, and federated learning. This review aims to consolidate current knowledge and guide future efforts in developing clinically relevant AI tools for personalized AD prognostication.

Robust Regularized Low-Rank Matrix Models for Regression and Classification

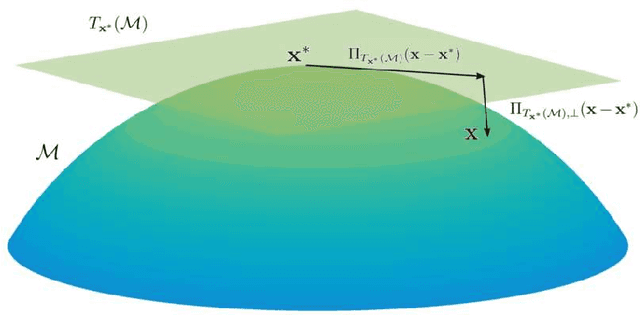
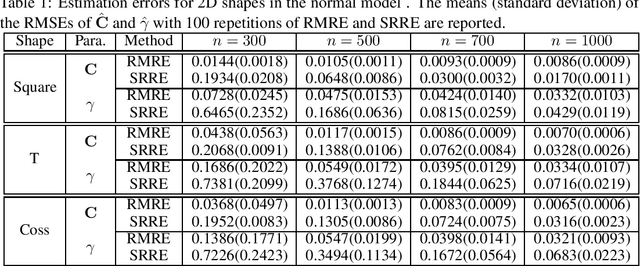
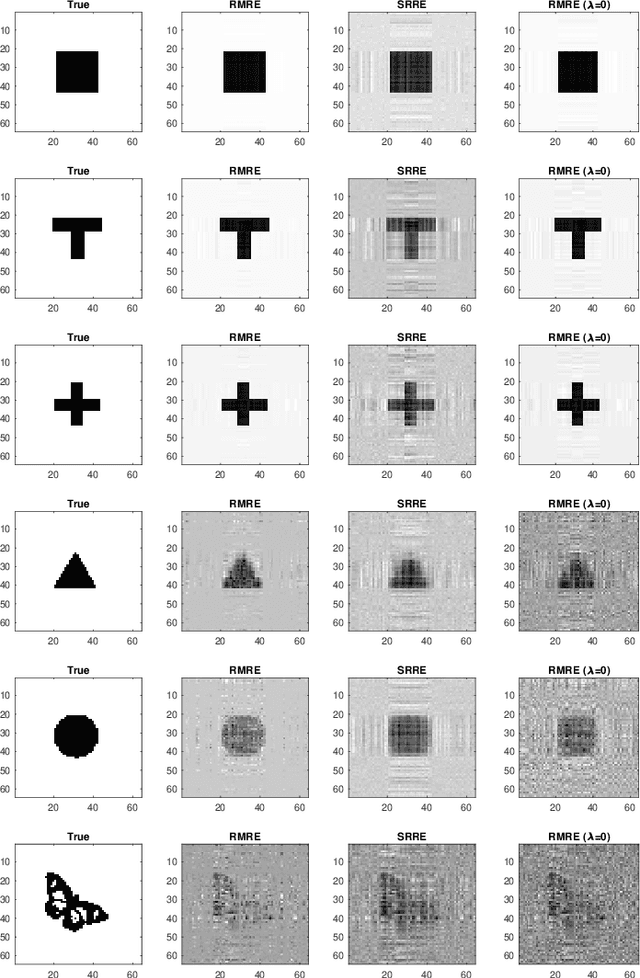
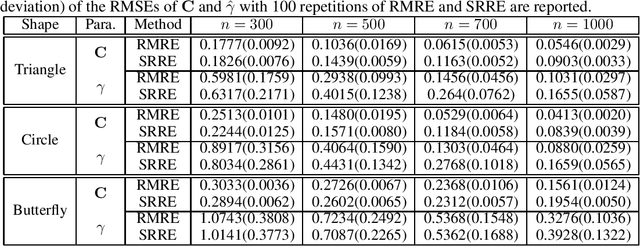
While matrix variate regression models have been studied in many existing works, classical statistical and computational methods for the analysis of the regression coefficient estimation are highly affected by high dimensional and noisy matrix-valued predictors. To address these issues, this paper proposes a framework of matrix variate regression models based on a rank constraint, vector regularization (e.g., sparsity), and a general loss function with three special cases considered: ordinary matrix regression, robust matrix regression, and matrix logistic regression. We also propose an alternating projected gradient descent algorithm. Based on analyzing our objective functions on manifolds with bounded curvature, we show that the algorithm is guaranteed to converge, all accumulation points of the iterates have estimation errors in the order of $O(1/\sqrt{n})$ asymptotically and substantially attaining the minimax rate. Our theoretical analysis can be applied to general optimization problems on manifolds with bounded curvature and can be considered an important technical contribution to this work. We validate the proposed method through simulation studies and real image data examples.

The Unsupervised Method of Vessel Movement Trajectory Prediction

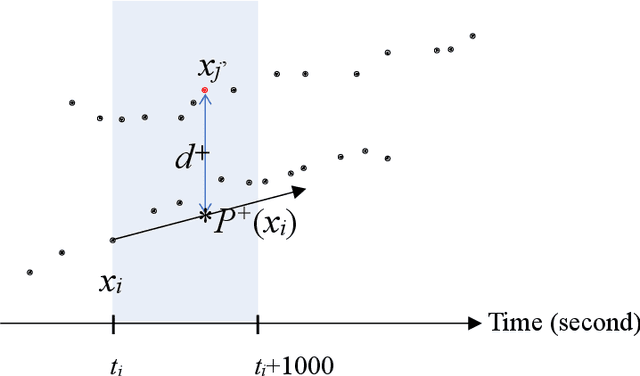
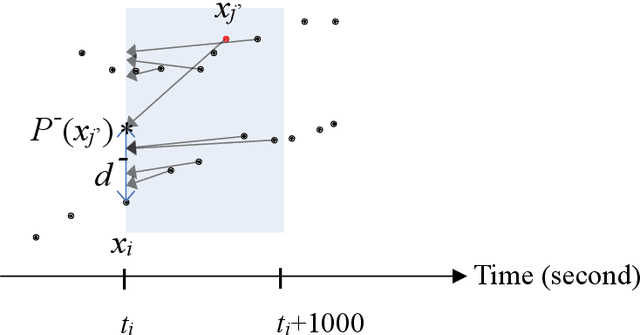
In real-world application scenarios, it is crucial for marine navigators and security analysts to predict vessel movement trajectories at sea based on the Automated Identification System (AIS) data in a given time span. This article presents an unsupervised method of ship movement trajectory prediction which represents the data in a three-dimensional space which consists of time difference between points, the scaled error distance between the tested and its predicted forward and backward locations, and the space-time angle. The representation feature space reduces the search scope for the next point to a collection of candidates which fit the local path prediction well, and therefore improve the accuracy. Unlike most statistical learning or deep learning methods, the proposed clustering-based trajectory reconstruction method does not require computationally expensive model training. This makes real-time reliable and accurate prediction feasible without using a training set. Our results show that the most prediction trajectories accurately consist of the true vessel paths.