Dual-Function Radar-Communication Beamforming with Outage Probability Metric

The integrated design of communication and sensing may offer a potential solution to address spectrum congestion. In this work, we develop a beamforming method for a dual-function radar-communication system, where the transmit signal is used for both radar surveillance and communication with multiple downlink users, despite imperfect channel state information (CSI). We focus on two scenarios of interest: radar-centric and communication-centric. In the radar-centric scenario, the primary goal is to optimize radar performance while attaining acceptable communication performance. To this end, we minimize a weighted sum of the mean-squared error in achieving a desired beampattern and a mean-squared cross correlation of the radar returns from directions of interest (DOI). We also seek to ensure that the probability of outage for the communication users remains below a desired threshold. In the communication-centric scenario, our main objective is to minimize the maximum probability of outage among the communication users while keeping the aforementioned radar metrics below a desired threshold. Both optimization problems are stochastic and untractable. We first take advantage of central limit theorem to obtain deterministic non-convex problems and then consider relaxations of these problems in the form of semidefinite programs with rank-1 constraints. We provide numerical experiments demonstrating the effectiveness of the proposed designs.

Manifold Learning for Knowledge Discovery and Intelligent Inverse Design of Photonic Nanostructures: Breaking the Geometric Complexity

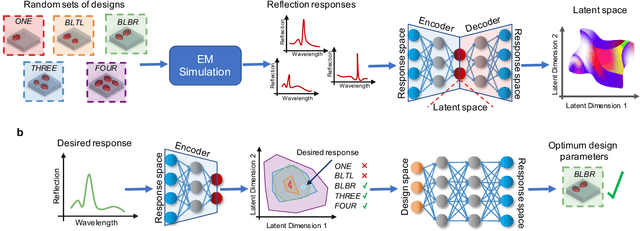
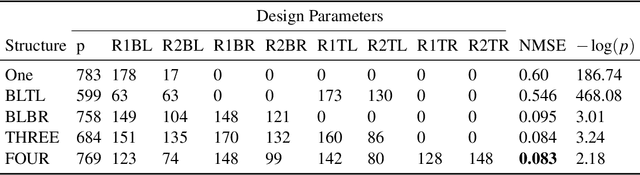
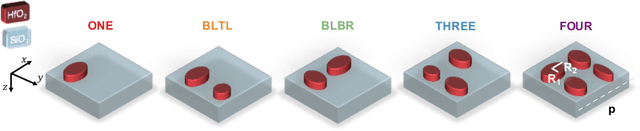
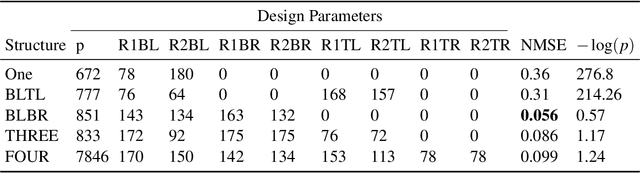
Here, we present a new approach based on manifold learning for knowledge discovery and inverse design with minimal complexity in photonic nanostructures. Our approach builds on studying sub-manifolds of responses of a class of nanostructures with different design complexities in the latent space to obtain valuable insight about the physics of device operation to guide a more intelligent design. In contrast to the current methods for inverse design of photonic nanostructures, which are limited to pre-selected and usually over-complex structures, we show that our method allows evolution from an initial design towards the simplest structure while solving the inverse problem.