Sequential Bayesian Design for Efficient Surrogate Construction in the Inversion of Darcy Flows

Inverse problems governed by partial differential equations (PDEs) play a crucial role in various fields, including computational science, image processing, and engineering. Particularly, Darcy flow equation is a fundamental equation in fluid mechanics, which plays a crucial role in understanding fluid flow through porous media. Bayesian methods provide an effective approach for solving PDEs inverse problems, while their numerical implementation requires numerous evaluations of computationally expensive forward solvers. Therefore, the adoption of surrogate models with lower computational costs is essential. However, constructing a globally accurate surrogate model for high-dimensional complex problems demands high model capacity and large amounts of data. To address this challenge, this study proposes an efficient locally accurate surrogate that focuses on the high-probability regions of the true likelihood in inverse problems, with relatively low model complexity and few training data requirements. Additionally, we introduce a sequential Bayesian design strategy to acquire the proposed surrogate since the high-probability region of the likelihood is unknown. The strategy treats the posterior evolution process of sequential Bayesian design as a Gaussian process, enabling algorithmic acceleration through one-step ahead prior. The complete algorithmic framework is referred to as Sequential Bayesian design for locally accurate surrogate (SBD-LAS). Finally, three experiments based the Darcy flow equation demonstrate the advantages of the proposed method in terms of both inversion accuracy and computational speed.

Active Learning for Transition State Calculation

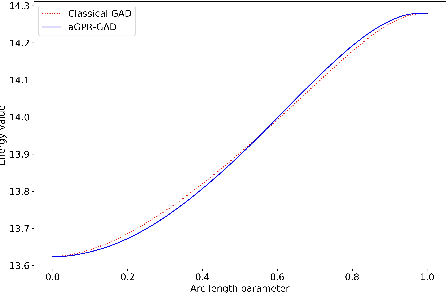
The transition state (TS) calculation is a grand challenge for computational intensive energy function. The traditional methods need to evaluate the gradients of the energy function at a very large number of locations. To reduce the number of expensive computations of the true gradients, we propose an active learning framework consisting of a statistical surrogate model, Gaussian process regression (GPR) for the energy function, and a single-walker dynamics method, gentle accent dynamics (GAD), for the saddle-type transition states. TS is detected by the GAD applied to the GPR surrogate for the gradient vector and the Hessian matrix. Our key ingredient for efficiency improvements is an active learning method which sequentially designs the most informative locations and takes evaluations of the original model at these locations to train GPR. We formulate this active learning task as the optimal experimental design problem and propose a very efficient sample-based sub-optimal criterion to construct the optimal locations. We show that the new method significantly decreases the required number of energy or force evaluations of the original model.

Adaptive Gaussian process approximation for Bayesian inference with expensive likelihood functions

We consider Bayesian inference problems with computationally intensive likelihood functions. We propose a Gaussian process (GP) based method to approximate the joint distribution of the unknown parameters and the data. In particular, we write the joint density approximately as a product of an approximate posterior density and an exponentiated GP surrogate. We then provide an adaptive algorithm to construct such an approximation, where an active learning method is used to choose the design points. With numerical examples, we illustrate that the proposed method has competitive performance against existing approaches for Bayesian computation.