Bringing freedom in variable choice when searching counter-examples in floating point programs

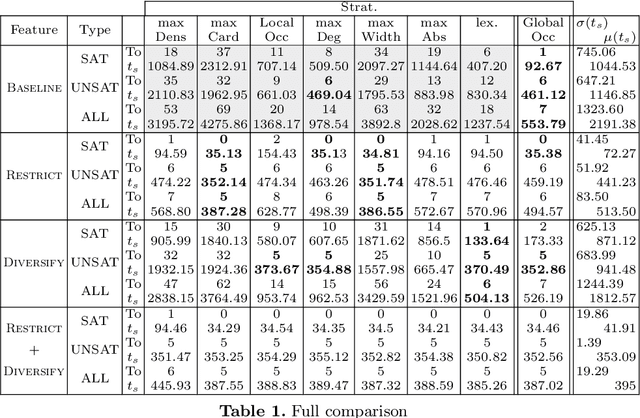
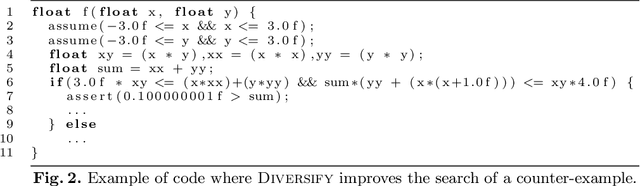
Program verification techniques typically focus on finding counter-examples that violate properties of a program. Constraint programming offers a convenient way to verify programs by modeling their state transformations and specifying searches that seek counter-examples. Floating-point computations present additional challenges for verification given the semantic subtleties of floating point arithmetic. % This paper focuses on search strategies for CSPs using floating point numbers constraint systems and dedicated to program verification. It introduces a new search heuristic based on the global number of occurrences that outperforms state-of-the-art strategies. More importantly, it demonstrates that a new technique that only branches on input variables of the verified program improve performance. It composes with a diversification technique that prevents the selection of the same variable within a fixed horizon further improving performances and reduces disparities between various variable choice heuristics. The result is a robust methodology that can tailor the search strategy according to the sought properties of the counter example.

An efficient constraint based framework forhandling floating point SMT problems

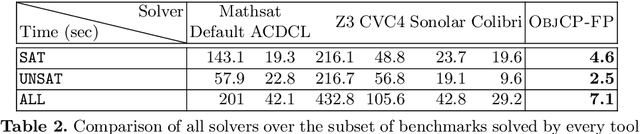
This paper introduces the 2019 version of \us{}, a novel Constraint Programming framework for floating point verification problems expressed with the SMT language of SMTLIB. SMT solvers decompose their task by delegating to specific theories (e.g., floating point, bit vectors, arrays, ...) the task to reason about combinatorial or otherwise complex constraints for which the SAT encoding would be cumbersome or ineffective. This decomposition and encoding processes lead to the obfuscation of the high-level constraints and a loss of information on the structure of the combinatorial model. In \us{}, constraints over the floats are first class objects, and the purpose is to expose and exploit structures of floating point domains to enhance the search process. A symbolic phase rewrites each SMTLIB instance to elementary constraints, and eliminates auxiliary variables whose presence is counterproductive. A diversification technique within the search steers it away from costly enumerations in unproductive areas of the search space. The empirical evaluation demonstrates that the 2019 version of \us{} is competitive on computationally challenging floating point benchmarks that induce significant search efforts even for other CP solvers. It highlights that the ability to harness both inference and search is critical. Indeed, it yields a factor 3 improvement over Colibri and is up to 10 times faster than SMT solvers. The evaluation was conducted over 214 benchmarks (The Griggio suite) which is a standard within SMTLIB.