An extension of the angular synchronization problem to the heterogeneous setting

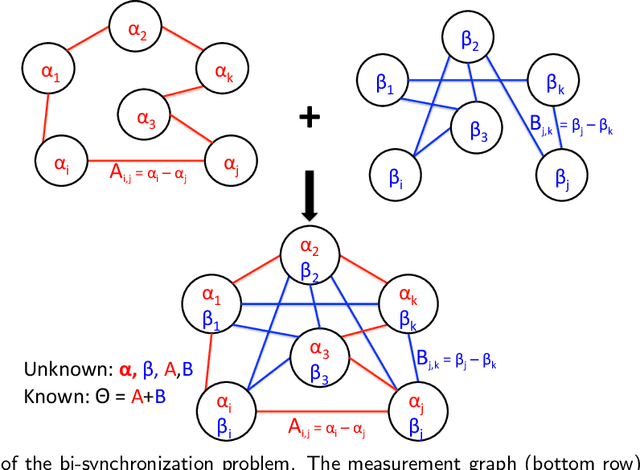
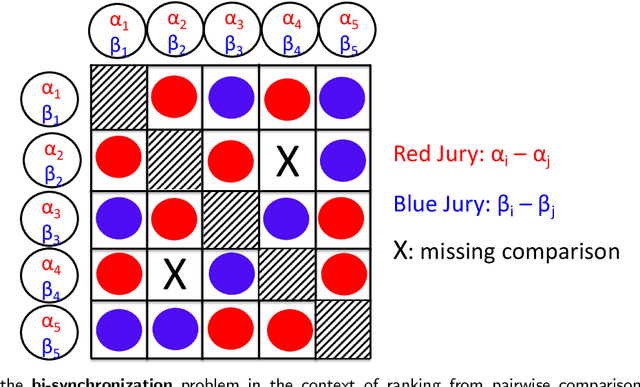
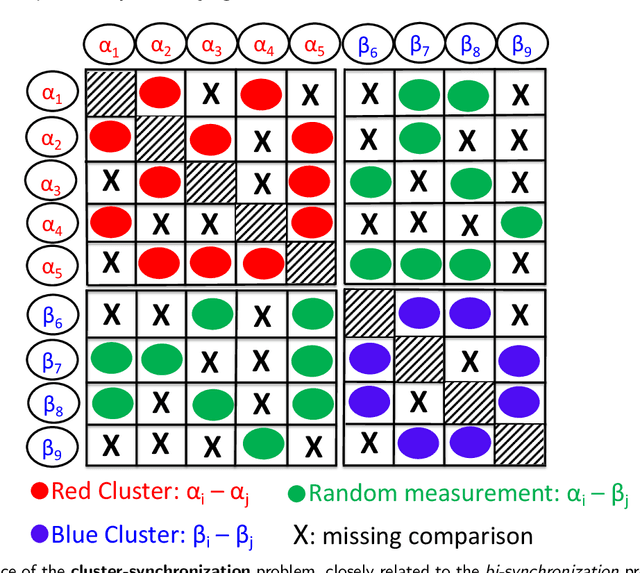
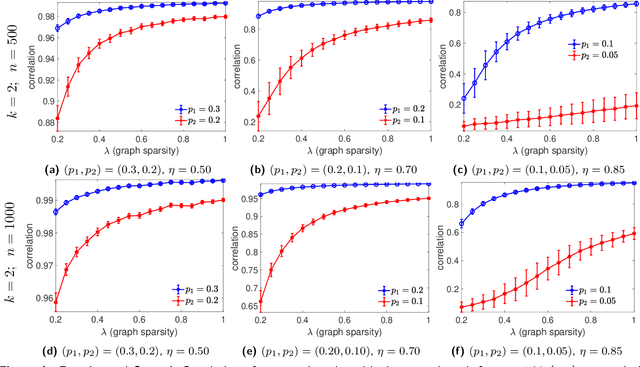
Given an undirected measurement graph $G = ([n], E)$, the classical angular synchronization problem consists of recovering unknown angles $\theta_1,\dots,\theta_n$ from a collection of noisy pairwise measurements of the form $(\theta_i - \theta_j) \mod 2\pi$, for each $\{i,j\} \in E$. This problem arises in a variety of applications, including computer vision, time synchronization of distributed networks, and ranking from preference relationships. In this paper, we consider a generalization to the setting where there exist $k$ unknown groups of angles $\theta_{l,1}, \dots,\theta_{l,n}$, for $l=1,\dots,k$. For each $ \{i,j\} \in E$, we are given noisy pairwise measurements of the form $\theta_{\ell,i} - \theta_{\ell,j}$ for an unknown $\ell \in \{1,2,\ldots,k\}$. This can be thought of as a natural extension of the angular synchronization problem to the heterogeneous setting of multiple groups of angles, where the measurement graph has an unknown edge-disjoint decomposition $G = G_1 \cup G_2 \ldots \cup G_k$, where the $G_i$'s denote the subgraphs of edges corresponding to each group. We propose a probabilistic generative model for this problem, along with a spectral algorithm for which we provide a detailed theoretical analysis in terms of robustness against both sampling sparsity and noise. The theoretical findings are complemented by a comprehensive set of numerical experiments, showcasing the efficacy of our algorithm under various parameter regimes. Finally, we consider an application of bi-synchronization to the graph realization problem, and provide along the way an iterative graph disentangling procedure that uncovers the subgraphs $G_i$, $i=1,\ldots,k$ which is of independent interest, as it is shown to improve the final recovery accuracy across all the experiments considered.

Regularized spectral methods for clustering signed networks

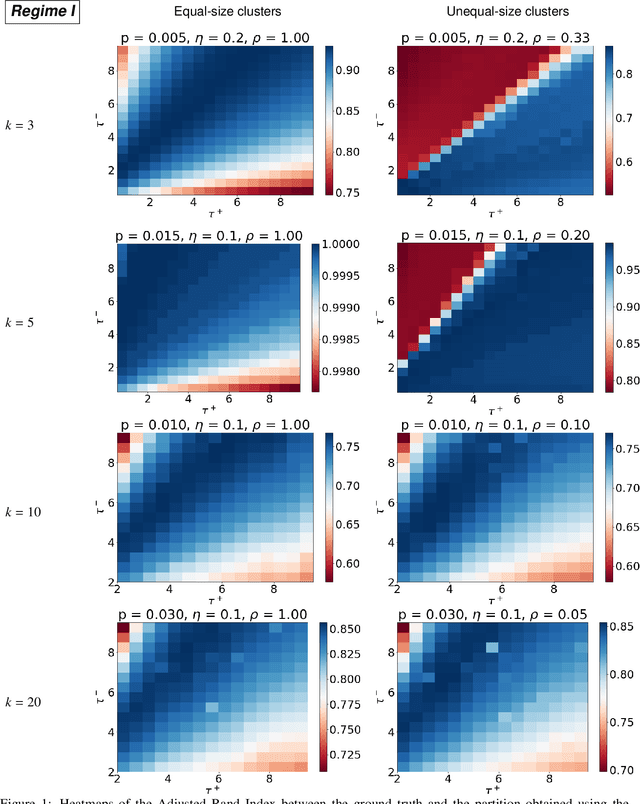
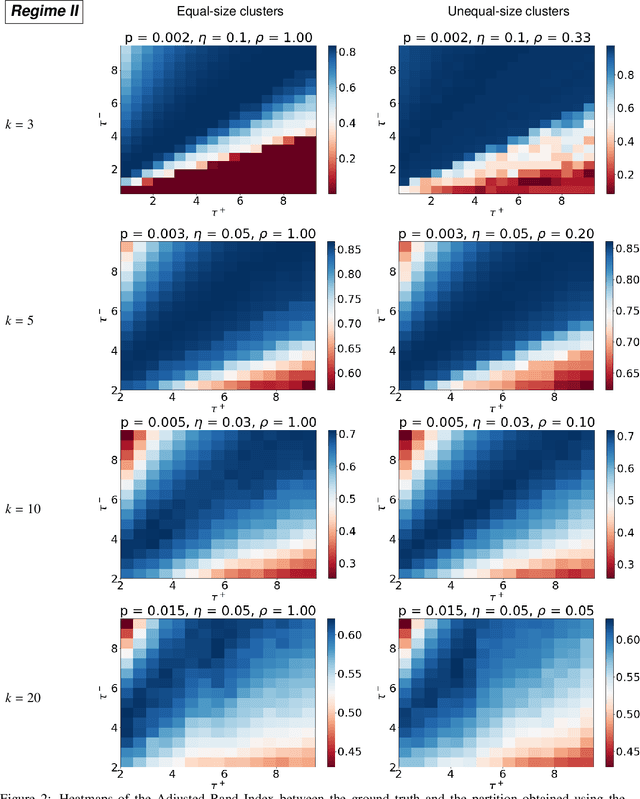
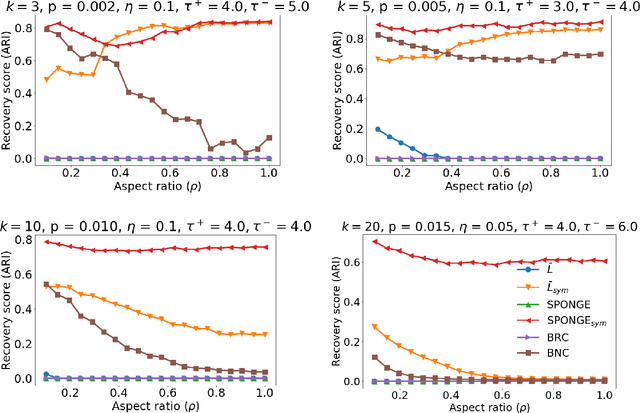
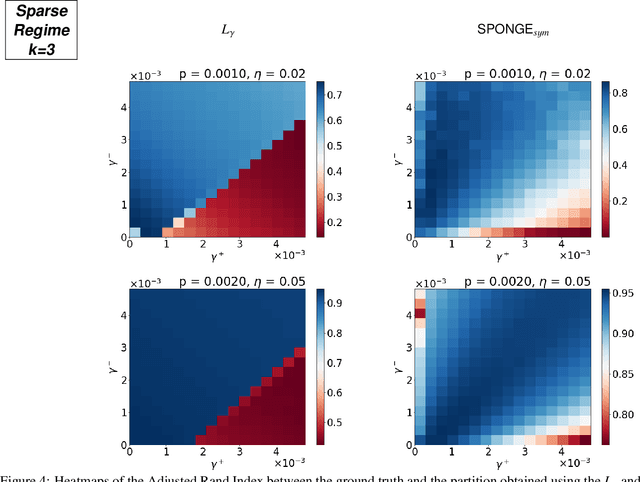
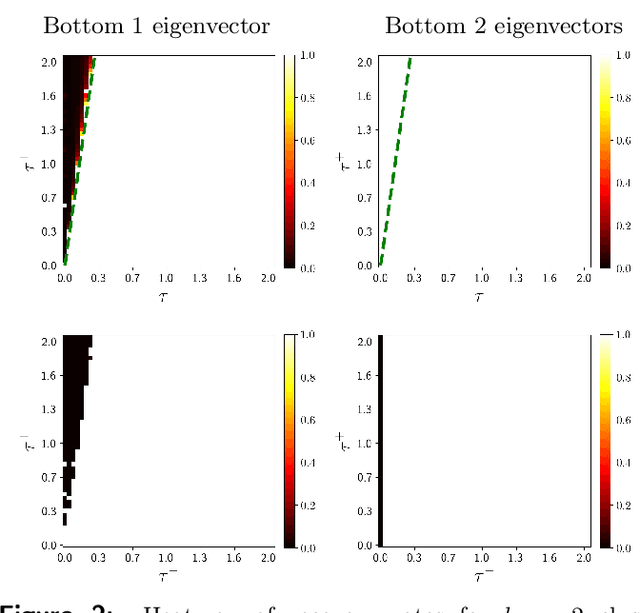
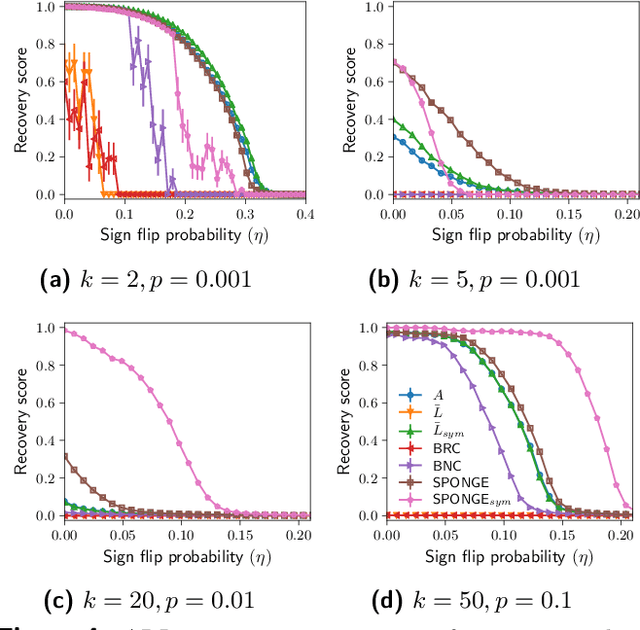
We study the problem of $k$-way clustering in signed graphs. Considerable attention in recent years has been devoted to analyzing and modeling signed graphs, where the affinity measure between nodes takes either positive or negative values. Recently, Cucuringu et al. [CDGT 2019] proposed a spectral method, namely SPONGE (Signed Positive over Negative Generalized Eigenproblem), which casts the clustering task as a generalized eigenvalue problem optimizing a suitably defined objective function. This approach is motivated by social balance theory, where the clustering task aims to decompose a given network into disjoint groups, such that individuals within the same group are connected by as many positive edges as possible, while individuals from different groups are mainly connected by negative edges. Through extensive numerical simulations, SPONGE was shown to achieve state-of-the-art empirical performance. On the theoretical front, [CDGT 2019] analyzed SPONGE and the popular Signed Laplacian method under the setting of a Signed Stochastic Block Model (SSBM), for $k=2$ equal-sized clusters, in the regime where the graph is moderately dense. In this work, we build on the results in [CDGT 2019] on two fronts for the normalized versions of SPONGE and the Signed Laplacian. Firstly, for both algorithms, we extend the theoretical analysis in [CDGT 2019] to the general setting of $k \geq 2$ unequal-sized clusters in the moderately dense regime. Secondly, we introduce regularized versions of both methods to handle sparse graphs -- a regime where standard spectral methods underperform -- and provide theoretical guarantees under the same SSBM model. To the best of our knowledge, regularized spectral methods have so far not been considered in the setting of clustering signed graphs. We complement our theoretical results with an extensive set of numerical experiments on synthetic data.

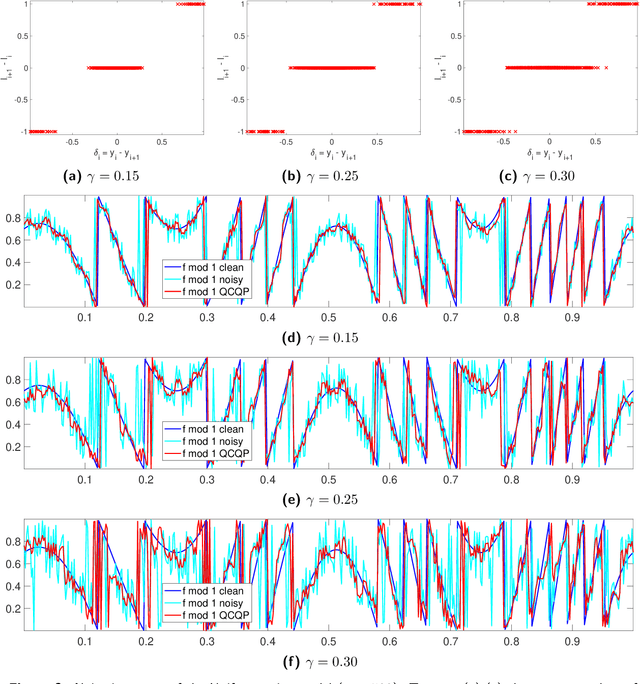
Error analysis for denoising smooth modulo signals on a graph

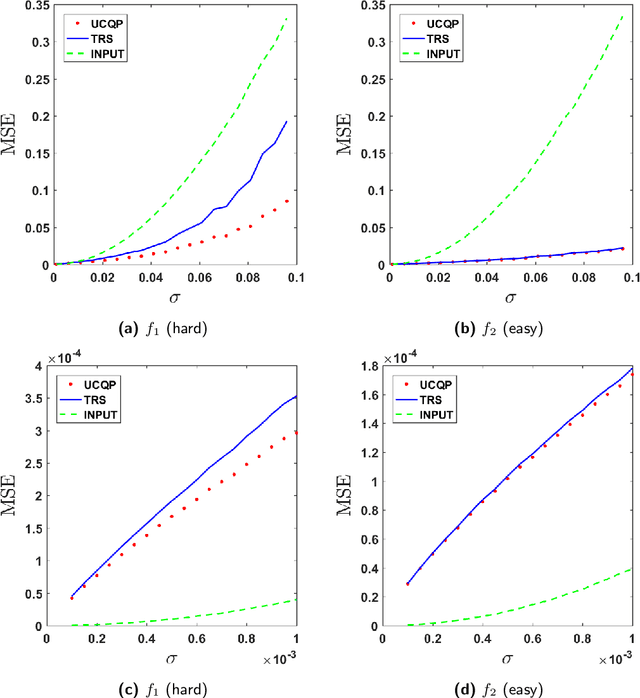
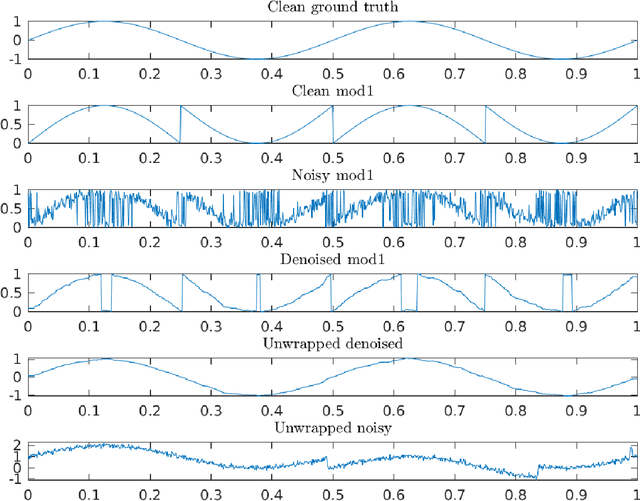
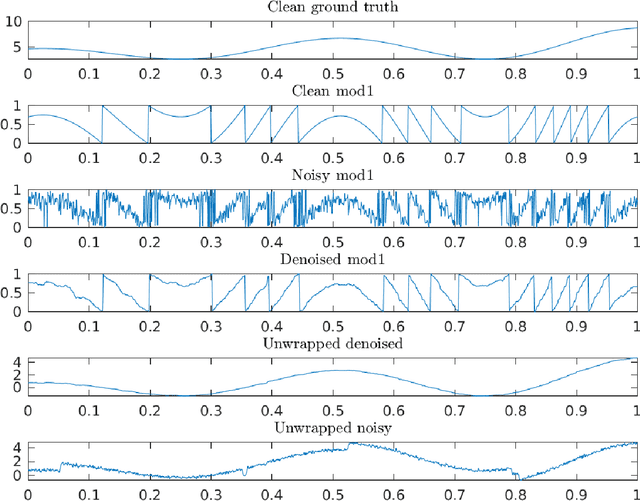
In many applications, we are given access to noisy modulo samples of a smooth function with the goal being to robustly unwrap the samples, i.e., to estimate the original samples of the function. In a recent work, Cucuringu and Tyagi proposed denoising the modulo samples by first representing them on the unit complex circle and then solving a smoothness regularized least squares problem -- the smoothness measured w.r.t the Laplacian of a suitable proximity graph $G$ -- on the product manifold of unit circles. This problem is a quadratically constrained quadratic program (QCQP) which is nonconvex, hence they proposed solving its sphere-relaxation leading to a trust region subproblem (TRS). In terms of theoretical guarantees, $\ell_2$ error bounds were derived for (TRS). These bounds are however weak in general and do not really demonstrate the denoising performed by (TRS). In this work, we analyse the (TRS) as well as an unconstrained relaxation of (QCQP). For both these estimators we provide a refined analysis in the setting of Gaussian noise and derive noise regimes where they provably denoise the modulo observations w.r.t the $\ell_2$ norm. The analysis is performed in a general setting where $G$ is any connected graph.

Denoising modulo samples: k-NN regression and tightness of SDP relaxation

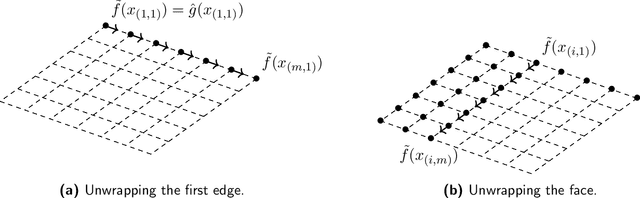
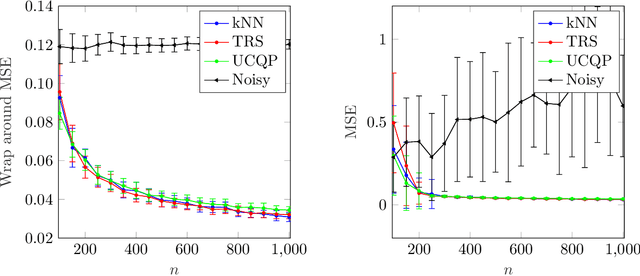
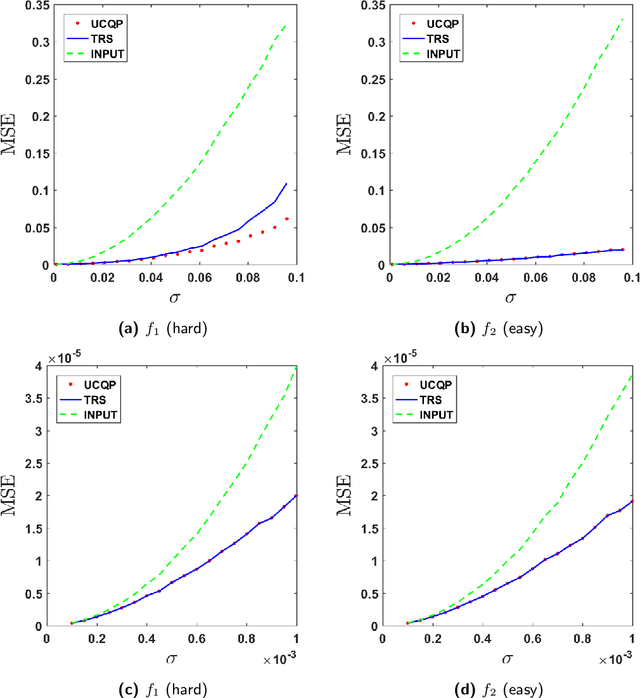
Many modern applications involve the acquisition of noisy modulo samples of a function $f$, with the goal being to recover estimates of the original samples of $f$. For a Lipschitz function $f:[0,1]^d \to \mathbb{R}$, suppose we are given the samples $y_i = (f(x_i) + \eta_i)\bmod 1; \quad i=1,\dots,n$ where $\eta_i$ denotes noise. Assuming $\eta_i$ are zero-mean i.i.d Gaussian's, and $x_i$'s form a uniform grid, we derive a two-stage algorithm that recovers estimates of the samples $f(x_i)$ with a uniform error rate $O((\frac{\log n}{n})^{\frac{1}{d+2}})$ holding with high probability. The first stage involves embedding the points on the unit complex circle, and obtaining denoised estimates of $f(x_i)\bmod 1$ via a $k$NN (nearest neighbor) estimator. The second stage involves a sequential unwrapping procedure which unwraps the denoised mod $1$ estimates from the first stage. Recently, Cucuringu and Tyagi proposed an alternative way of denoising modulo $1$ data which works with their representation on the unit complex circle. They formulated a smoothness regularized least squares problem on the product manifold of unit circles, where the smoothness is measured with respect to the Laplacian of a proximity graph $G$ involving the $x_i$'s. This is a nonconvex quadratically constrained quadratic program (QCQP) hence they proposed solving its semidefinite program (SDP) based relaxation. We derive sufficient conditions under which the SDP is a tight relaxation of the QCQP. Hence under these conditions, the global solution of QCQP can be obtained in polynomial time.

Ranking and synchronization from pairwise measurements via SVD

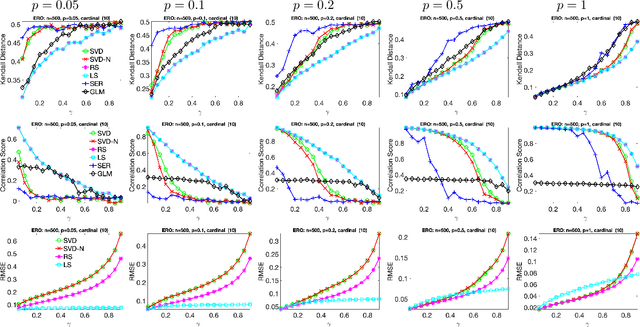
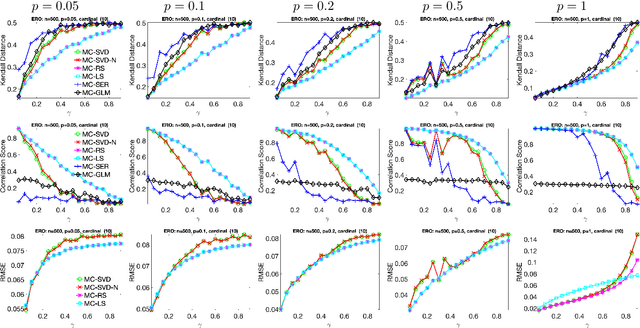
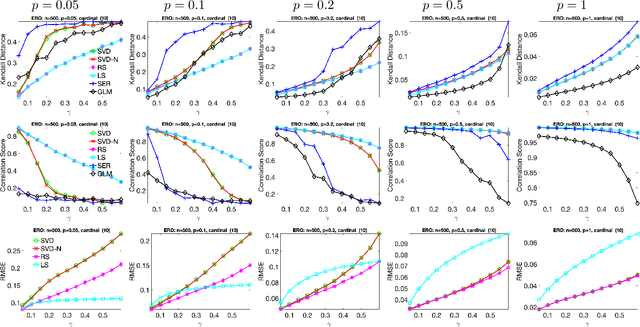
Given a measurement graph $G= (V,E)$ and an unknown signal $r \in \mathbb{R}^n$, we investigate algorithms for recovering $r$ from pairwise measurements of the form $r_i - r_j$; $\{i,j\} \in E$. This problem arises in a variety of applications, such as ranking teams in sports data and time synchronization of distributed networks. Framed in the context of ranking, the task is to recover the ranking of $n$ teams (induced by $r$) given a small subset of noisy pairwise rank offsets. We propose a simple SVD-based algorithmic pipeline for both the problem of time synchronization and ranking. We provide a detailed theoretical analysis in terms of robustness against both sampling sparsity and noise perturbations with outliers, using results from matrix perturbation and random matrix theory. Our theoretical findings are complemented by a detailed set of numerical experiments on both synthetic and real data, showcasing the competitiveness of our proposed algorithms with other state-of-the-art methods.

SPONGE: A generalized eigenproblem for clustering signed networks

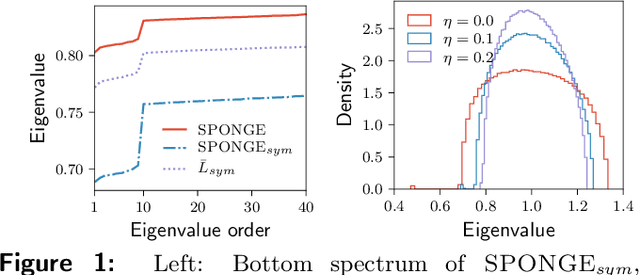
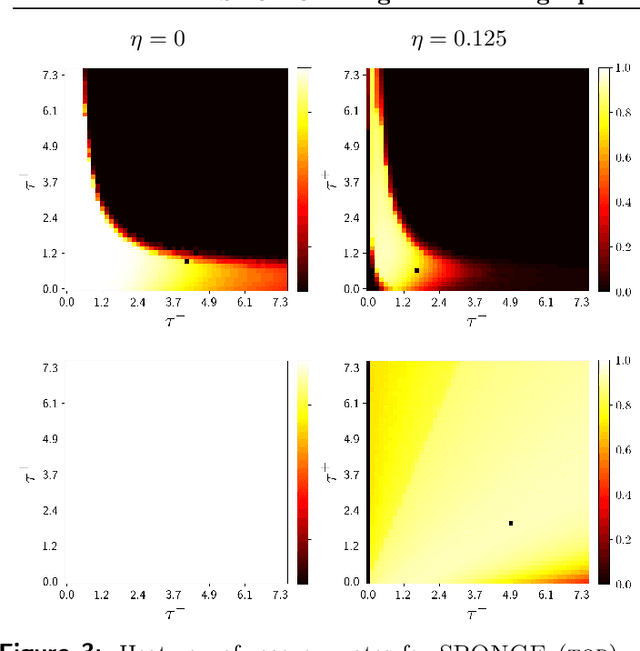
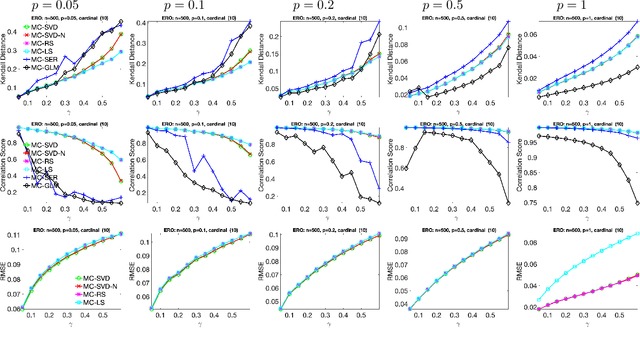
We introduce a principled and theoretically sound spectral method for $k$-way clustering in signed graphs, where the affinity measure between nodes takes either positive or negative values. Our approach is motivated by social balance theory, where the task of clustering aims to decompose the network into disjoint groups, such that individuals within the same group are connected by as many positive edges as possible, while individuals from different groups are connected by as many negative edges as possible. Our algorithm relies on a generalized eigenproblem formulation inspired by recent work on constrained clustering. We provide theoretical guarantees for our approach in the setting of a signed stochastic block model, by leveraging tools from matrix perturbation theory and random matrix theory. An extensive set of numerical experiments on both synthetic and real data shows that our approach compares favorably with state-of-the-art methods for signed clustering, especially for large number of clusters and sparse measurement graphs.

On denoising modulo 1 samples of a function

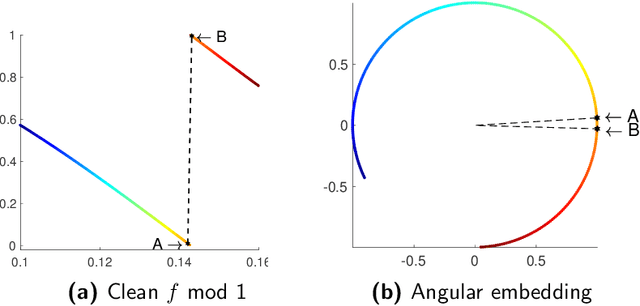
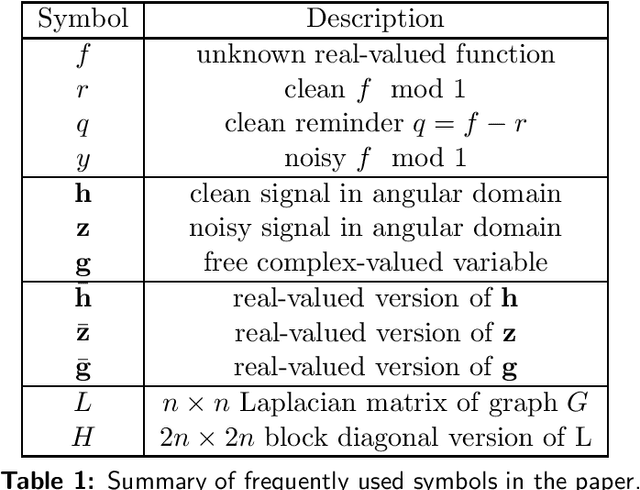
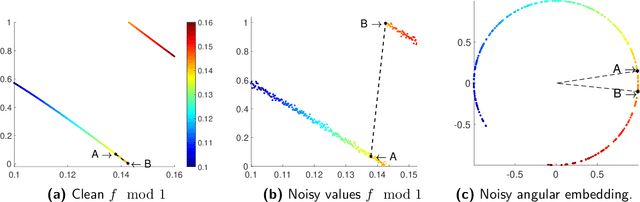
Consider an unknown smooth function $f: [0,1] \rightarrow \mathbb{R}$, and say we are given $n$ noisy$\mod 1$ samples of $f$, i.e., $y_i = (f(x_i) + \eta_i)\mod 1$ for $x_i \in [0,1]$, where $\eta_i$ denotes noise. Given the samples $(x_i,y_i)_{i=1}^{n}$ our goal is to recover smooth, robust estimates of the clean samples $f(x_i) \bmod 1$. We formulate a natural approach for solving this problem which works with representations of mod 1 values over the unit circle. This amounts to solving a quadratically constrained quadratic program (QCQP) with non-convex constraints involving points lying on the unit circle. Our proposed approach is based on solving its relaxation which is a trust-region sub-problem, and hence solvable efficiently. We demonstrate its robustness to noise % of our approach via extensive simulations on several synthetic examples, and provide a detailed theoretical analysis.

Provably robust estimation of modulo 1 samples of a smooth function with applications to phase unwrapping

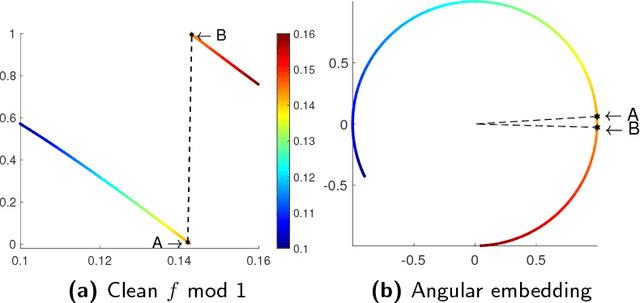
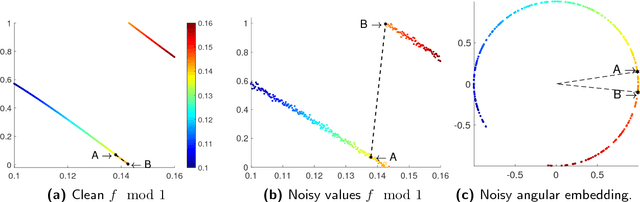
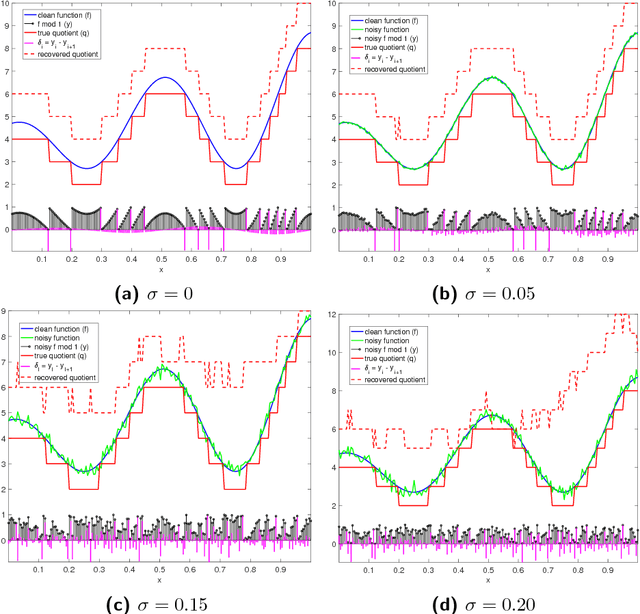
Consider an unknown smooth function $f: [0,1]^d \rightarrow \mathbb{R}$, and say we are given $n$ noisy mod 1 samples of $f$, i.e., $y_i = (f(x_i) + \eta_i)\mod 1$, for $x_i \in [0,1]^d$, where $\eta_i$ denotes the noise. Given the samples $(x_i,y_i)_{i=1}^{n}$, our goal is to recover smooth, robust estimates of the clean samples $f(x_i) \bmod 1$. We formulate a natural approach for solving this problem, which works with angular embeddings of the noisy mod 1 samples over the unit circle, inspired by the angular synchronization framework. This amounts to solving a smoothness regularized least-squares problem -- a quadratically constrained quadratic program (QCQP) -- where the variables are constrained to lie on the unit circle. Our approach is based on solving its relaxation, which is a trust-region sub-problem and hence solvable efficiently. We provide theoretical guarantees demonstrating its robustness to noise for adversarial, and random Gaussian and Bernoulli noise models. To the best of our knowledge, these are the first such theoretical results for this problem. We demonstrate the robustness and efficiency of our approach via extensive numerical simulations on synthetic data, along with a simple least-squares solution for the unwrapping stage, that recovers the original samples of $f$ (up to a global shift). It is shown to perform well at high levels of noise, when taking as input the denoised modulo $1$ samples. Finally, we also consider two other approaches for denoising the modulo 1 samples that leverage tools from Riemannian optimization on manifolds, including a Burer-Monteiro approach for a semidefinite programming relaxation of our formulation. For the two-dimensional version of the problem, which has applications in radar interferometry, we are able to solve instances of real-world data with a million sample points in under 10 seconds, on a personal laptop.

Stochastic continuum armed bandit problem of few linear parameters in high dimensions

We consider a stochastic continuum armed bandit problem where the arms are indexed by the $\ell_2$ ball $B_{d}(1+\nu)$ of radius $1+\nu$ in $\mathbb{R}^d$. The reward functions $r :B_{d}(1+\nu) \rightarrow \mathbb{R}$ are considered to intrinsically depend on $k \ll d$ unknown linear parameters so that $r(\mathbf{x}) = g(\mathbf{A} \mathbf{x})$ where $\mathbf{A}$ is a full rank $k \times d$ matrix. Assuming the mean reward function to be smooth we make use of results from low-rank matrix recovery literature and derive an efficient randomized algorithm which achieves a regret bound of $O(C(k,d) n^{\frac{1+k}{2+k}} (\log n)^{\frac{1}{2+k}})$ with high probability. Here $C(k,d)$ is at most polynomial in $d$ and $k$ and $n$ is the number of rounds or the sampling budget which is assumed to be known beforehand.

Algorithms for Learning Sparse Additive Models with Interactions in High Dimensions

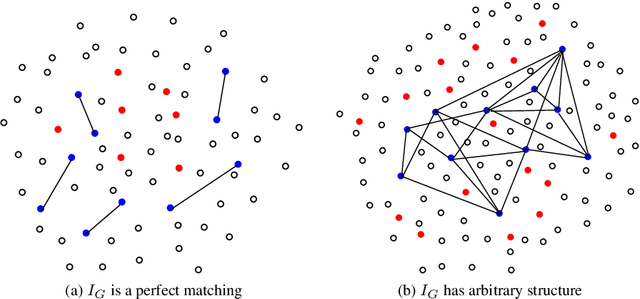
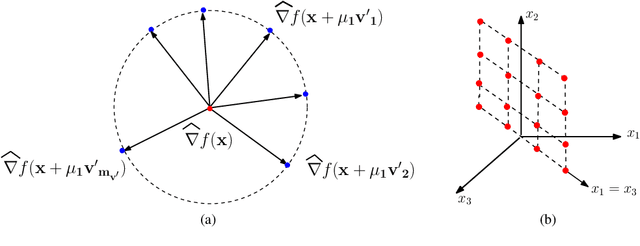
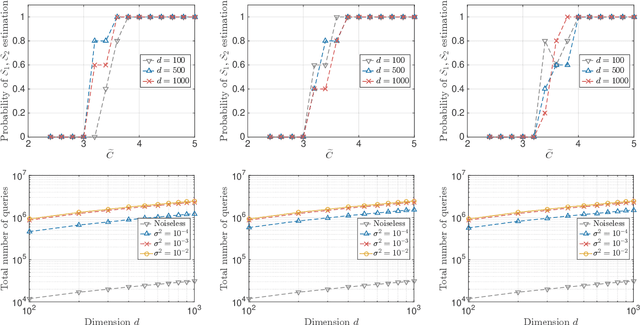
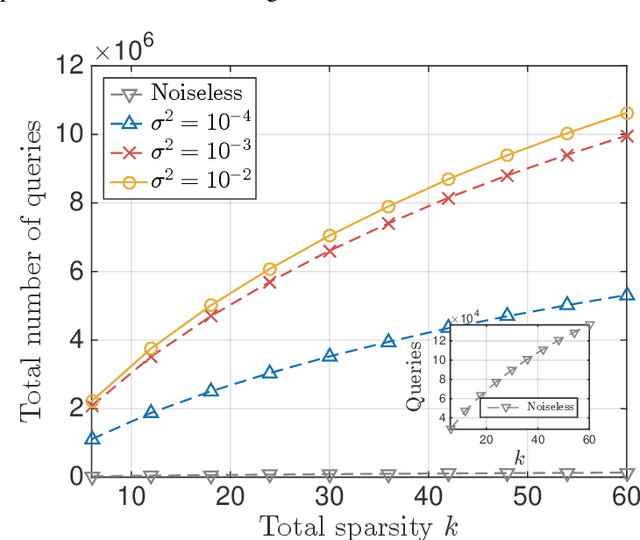
A function $f: \mathbb{R}^d \rightarrow \mathbb{R}$ is a Sparse Additive Model (SPAM), if it is of the form $f(\mathbf{x}) = \sum_{l \in \mathcal{S}}\phi_{l}(x_l)$ where $\mathcal{S} \subset [d]$, $|\mathcal{S}| \ll d$. Assuming $\phi$'s, $\mathcal{S}$ to be unknown, there exists extensive work for estimating $f$ from its samples. In this work, we consider a generalized version of SPAMs, that also allows for the presence of a sparse number of second order interaction terms. For some $\mathcal{S}_1 \subset [d], \mathcal{S}_2 \subset {[d] \choose 2}$, with $|\mathcal{S}_1| \ll d, |\mathcal{S}_2| \ll d^2$, the function $f$ is now assumed to be of the form: $\sum_{p \in \mathcal{S}_1}\phi_{p} (x_p) + \sum_{(l,l^{\prime}) \in \mathcal{S}_2}\phi_{(l,l^{\prime})} (x_l,x_{l^{\prime}})$. Assuming we have the freedom to query $f$ anywhere in its domain, we derive efficient algorithms that provably recover $\mathcal{S}_1,\mathcal{S}_2$ with finite sample bounds. Our analysis covers the noiseless setting where exact samples of $f$ are obtained, and also extends to the noisy setting where the queries are corrupted with noise. For the noisy setting in particular, we consider two noise models namely: i.i.d Gaussian noise and arbitrary but bounded noise. Our main methods for identification of $\mathcal{S}_2$ essentially rely on estimation of sparse Hessian matrices, for which we provide two novel compressed sensing based schemes. Once $\mathcal{S}_1, \mathcal{S}_2$ are known, we show how the individual components $\phi_p$, $\phi_{(l,l^{\prime})}$ can be estimated via additional queries of $f$, with uniform error bounds. Lastly, we provide simulation results on synthetic data that validate our theoretical findings.