Anomaly Detection by Effectively Leveraging Synthetic Images

Anomaly detection plays a vital role in industrial manufacturing. Due to the scarcity of real defect images, unsupervised approaches that rely solely on normal images have been extensively studied. Recently, diffusion-based generative models brought attention to training data synthesis as an alternative solution. In this work, we focus on a strategy to effectively leverage synthetic images to maximize the anomaly detection performance. Previous synthesis strategies are broadly categorized into two groups, presenting a clear trade-off. Rule-based synthesis, such as injecting noise or pasting patches, is cost-effective but often fails to produce realistic defect images. On the other hand, generative model-based synthesis can create high-quality defect images but requires substantial cost. To address this problem, we propose a novel framework that leverages a pre-trained text-guided image-to-image translation model and image retrieval model to efficiently generate synthetic defect images. Specifically, the image retrieval model assesses the similarity of the generated images to real normal images and filters out irrelevant outputs, thereby enhancing the quality and relevance of the generated defect images. To effectively leverage synthetic images, we also introduce a two stage training strategy. In this strategy, the model is first pre-trained on a large volume of images from rule-based synthesis and then fine-tuned on a smaller set of high-quality images. This method significantly reduces the cost for data collection while improving the anomaly detection performance. Experiments on the MVTec AD dataset demonstrate the effectiveness of our approach.

Few-Shot Class-Incremental Model Attribution Using Learnable Representation From CLIP-ViT Features

Recently, images that distort or fabricate facts using generative models have become a social concern. To cope with continuous evolution of generative artificial intelligence (AI) models, model attribution (MA) is necessary beyond just detection of synthetic images. However, current deep learning-based MA methods must be trained from scratch with new data to recognize unseen models, which is time-consuming and data-intensive. This work proposes a new strategy to deal with persistently emerging generative models. We adapt few-shot class-incremental learning (FSCIL) mechanisms for MA problem to uncover novel generative AI models. Unlike existing FSCIL approaches that focus on object classification using high-level information, MA requires analyzing low-level details like color and texture in synthetic images. Thus, we utilize a learnable representation from different levels of CLIP-ViT features. To learn an effective representation, we propose Adaptive Integration Module (AIM) to calculate a weighted sum of CLIP-ViT block features for each image, enhancing the ability to identify generative models. Extensive experiments show our method effectively extends from prior generative models to recent ones.

Matrix Completion from General Deterministic Sampling Patterns

Most of the existing works on provable guarantees for low-rank matrix completion algorithms rely on some unrealistic assumptions such that matrix entries are sampled randomly or the sampling pattern has a specific structure. In this work, we establish theoretical guarantee for the exact and approximate low-rank matrix completion problems which can be applied to any deterministic sampling schemes. For this, we introduce a graph having observed entries as its edge set, and investigate its graph properties involving the performance of the standard constrained nuclear norm minimization algorithm. We theoretically and experimentally show that the algorithm can be successful as the observation graph is well-connected and has similar node degrees. Our result can be viewed as an extension of the works by Bhojanapalli and Jain [2014] and Burnwal and Vidyasagar [2020], in which the node degrees of the observation graph were assumed to be the same. In particular, our theory significantly improves their results when the underlying matrix is symmetric.

Support Recovery in Sparse PCA with Non-Random Missing Data

We analyze a practical algorithm for sparse PCA on incomplete and noisy data under a general non-random sampling scheme. The algorithm is based on a semidefinite relaxation of the $\ell_1$-regularized PCA problem. We provide theoretical justification that under certain conditions, we can recover the support of the sparse leading eigenvector with high probability by obtaining a unique solution. The conditions involve the spectral gap between the largest and second-largest eigenvalues of the true data matrix, the magnitude of the noise, and the structural properties of the observed entries. The concepts of algebraic connectivity and irregularity are used to describe the structural properties of the observed entries. We empirically justify our theorem with synthetic and real data analysis. We also show that our algorithm outperforms several other sparse PCA approaches especially when the observed entries have good structural properties. As a by-product of our analysis, we provide two theorems to handle a deterministic sampling scheme, which can be applied to other matrix-related problems.

Support Recovery in Sparse PCA with Incomplete Data

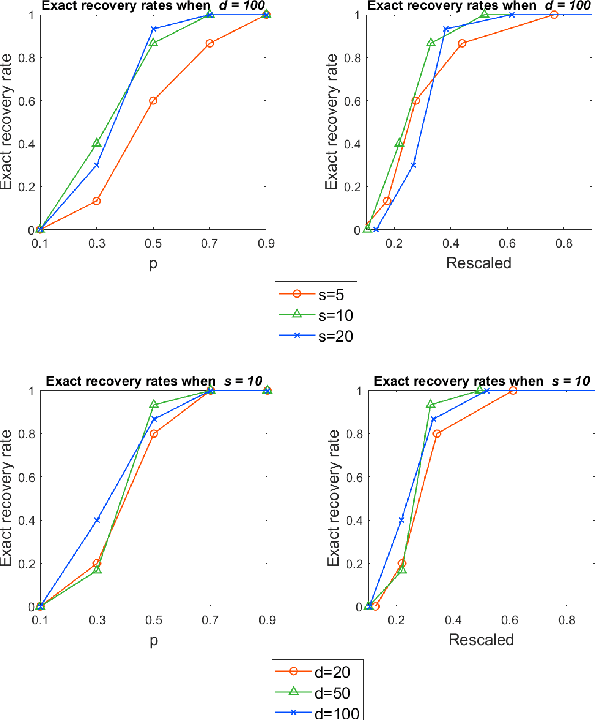
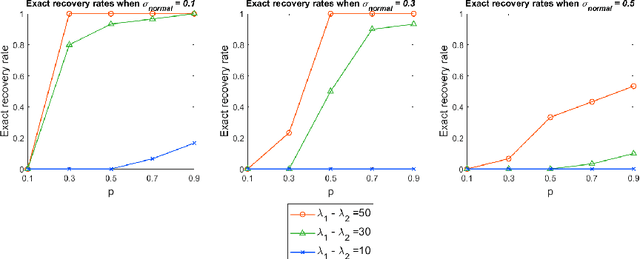
We study a practical algorithm for sparse principal component analysis (PCA) of incomplete and noisy data. Our algorithm is based on the semidefinite program (SDP) relaxation of the non-convex $l_1$-regularized PCA problem. We provide theoretical and experimental evidence that SDP enables us to exactly recover the true support of the sparse leading eigenvector of the unknown true matrix, despite only observing an incomplete (missing uniformly at random) and noisy version of it. We derive sufficient conditions for exact recovery, which involve matrix incoherence, the spectral gap between the largest and second-largest eigenvalues, the observation probability and the noise variance. We validate our theoretical results with incomplete synthetic data, and show encouraging and meaningful results on a gene expression dataset.

On the Fundamental Limits of Exact Inference in Structured Prediction

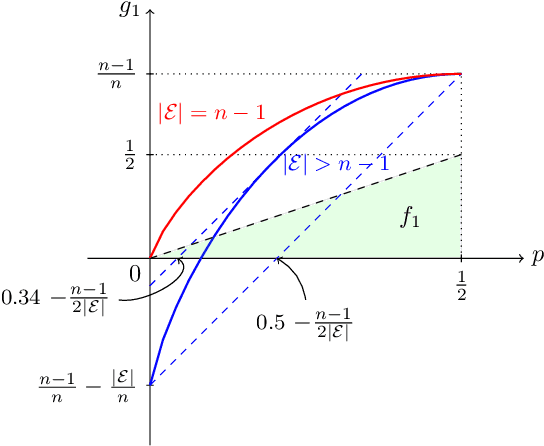
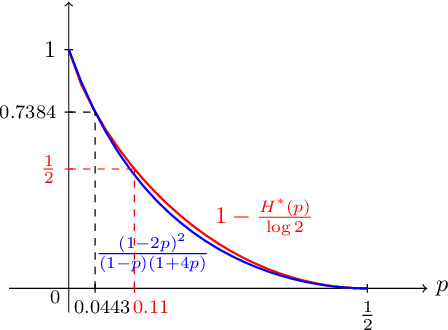
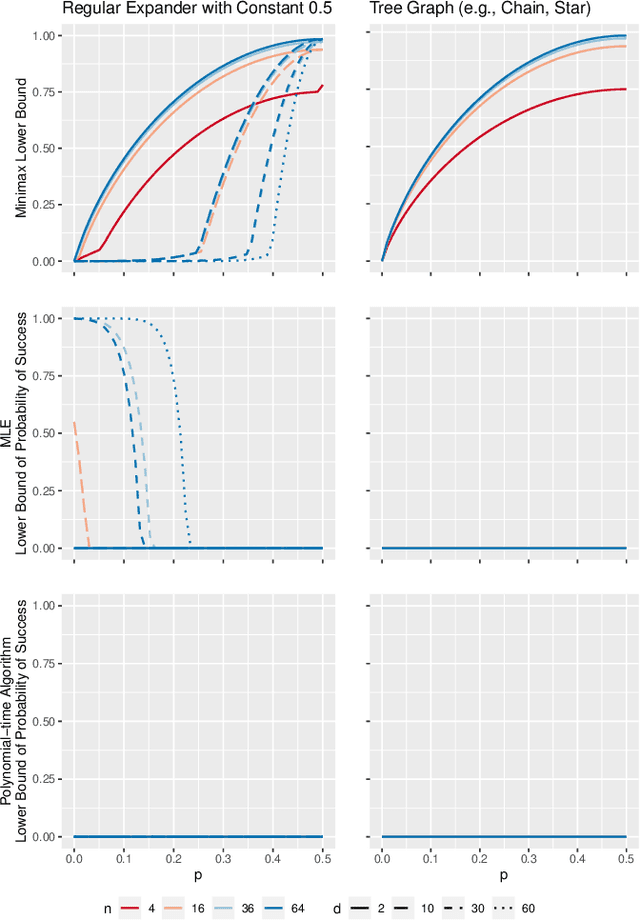
Inference is a main task in structured prediction and it is naturally modeled with a graph. In the context of Markov random fields, noisy observations corresponding to nodes and edges are usually involved, and the goal of exact inference is to recover the unknown true label for each node precisely. The focus of this paper is on the fundamental limits of exact recovery irrespective of computational efficiency, assuming the generative process proposed by Globerson et al. (2015). We derive the necessary condition for any algorithm and the sufficient condition for maximum likelihood estimation to achieve exact recovery with high probability, and reveal that the sufficient and necessary conditions are tight up to a logarithmic factor for a wide range of graphs. Finally, we show that there exists a gap between the fundamental limits and the performance of the computationally tractable method of Bello and Honorio (2019), which implies the need for further development of algorithms for exact inference.