Strong consistency and optimality of spectral clustering in symmetric binary non-uniform Hypergraph Stochastic Block Model

Consider the unsupervised classification problem in random hypergraphs under the non-uniform \emph{Hypergraph Stochastic Block Model} (HSBM) with two equal-sized communities ($n/2$), where each edge appears independently with some probability depending only on the labels of its vertices. In this paper, an \emph{information-theoretical} threshold for strong consistency is established. Below the threshold, every algorithm would misclassify at least two vertices with high probability, and the expected \emph{mismatch ratio} of the eigenvector estimator is upper bounded by $n$ to the power of minus the threshold. On the other hand, when above the threshold, despite the information loss induced by tensor contraction, one-stage spectral algorithms assign every vertex correctly with high probability when only given the contracted adjacency matrix, even if \emph{semidefinite programming} (SDP) fails in some scenarios. Moreover, strong consistency is achievable by aggregating information from all uniform layers, even if it is impossible when each layer is considered alone. Our conclusions are supported by both theoretical analysis and numerical experiments.

Exact recovery for the non-uniform Hypergraph Stochastic Block Model

Consider the community detection problem in random hypergraphs under the non-uniform hypergraph stochastic block model (HSBM), where each hyperedge appears independently with some given probability depending only on the labels of its vertices. We establish, for the first time in the literature, a sharp threshold for exact recovery under this non-uniform case, subject to minor constraints; in particular, we consider the model with $K$ classes as well as the symmetric binary model ($K=2$). One crucial point here is that by aggregating information from all the uniform layers, we may obtain exact recovery even in cases when this may appear impossible if each layer were considered alone. Two efficient algorithms that successfully achieve exact recovery above the threshold are provided. The theoretical analysis of our algorithms relies on the concentration and regularization of the adjacency matrix for non-uniform random hypergraphs, which could be of independent interest. We also address some open problems regarding parameter knowledge and estimation.

Partial recovery and weak consistency in the non-uniform hypergraph Stochastic Block Model

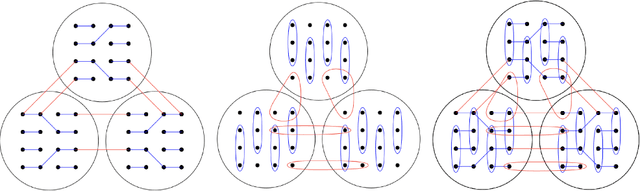
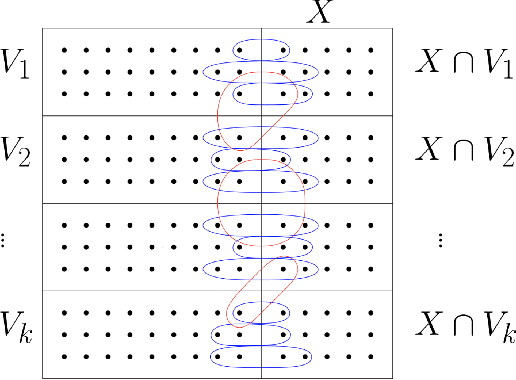
We consider the community detection problem in sparse random hypergraphs under the non-uniform hypergraph stochastic block model (HSBM), a general model of random networks with community structure and higher-order interactions. When the random hypergraph has bounded expected degrees, we provide a spectral algorithm that outputs a partition with at least a $\gamma$ fraction of the vertices classified correctly, where $\gamma\in (0.5,1)$ depends on the signal-to-noise ratio (SNR) of the model. When the SNR grows slowly as the number of vertices goes to infinity, our algorithm achieves weak consistency, which improves the previous results in Ghoshdastidar and Dukkipati (2017) for non-uniform HSBMs. Our spectral algorithm consists of three major steps: (1) Hyperedge selection: select hyperedges of certain sizes to provide the maximal signal-to-noise ratio for the induced sub-hypergraph; (2) Spectral partition: construct a regularized adjacency matrix and obtain an approximate partition based on singular vectors; (3) Correction and merging: incorporate the hyperedge information from adjacency tensors to upgrade the error rate guarantee. The theoretical analysis of our algorithm relies on the concentration and regularization of the adjacency matrix for sparse non-uniform random hypergraphs, which can be of independent interest.