Data-Driven Learning of Geometric Scattering Networks

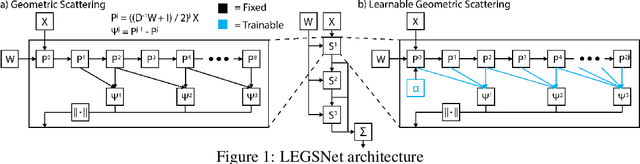
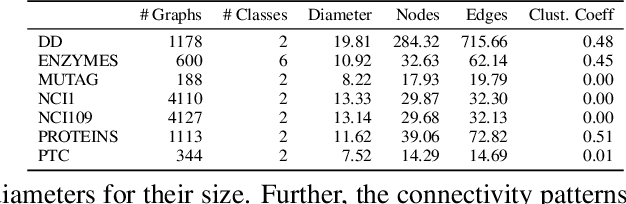
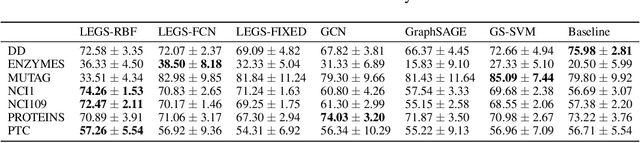
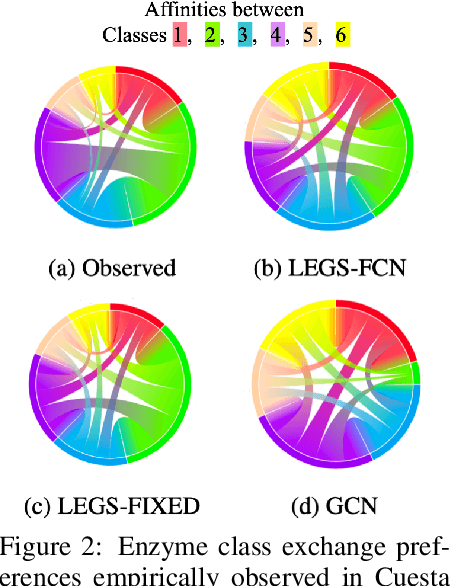
Graph neural networks (GNNs) in general, and graph convolutional networks (GCN) in particular, often rely on low-pass graph filters to incorporate geometric information in the form of local smoothness over neighboring nodes. While this approach performs well on a surprising number of standard benchmarks, the efficacy of such models does not translate consistently to more complex domains, such as graph data in the biochemistry domain. We argue that these more complex domains require priors that encourage learning of band-pass and high-pass features rather than oversmoothed signals of standard GCN architectures. Here, we propose an alternative GNN architecture, based on a relaxation of recently proposed geometric scattering transforms, which consists of a cascade of graph wavelet filters. Our learned geometric scattering (LEGS) architecture adaptively tunes these wavelets and their scales to encourage band-pass features to emerge in learned representations. This results in a simplified GNN with significantly fewer learned parameters compared to competing methods. We demonstrate the predictive performance of our method on several biochemistry graph classification benchmarks, as well as the descriptive quality of its learned features in biochemical graph data exploration tasks. Our results show that the proposed LEGS network matches or outperforms popular GNNs, as well as the original geometric scattering construction, while also retaining certain mathematical properties of its handcrafted (nonlearned) design.

Extendable and invertible manifold learning with geometry regularized autoencoders

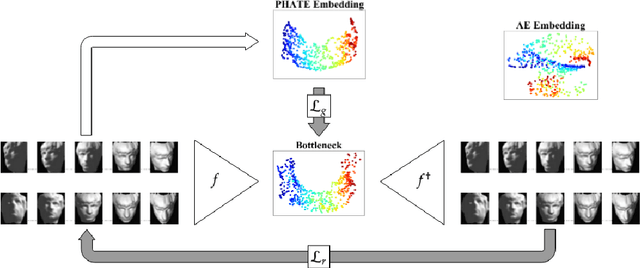
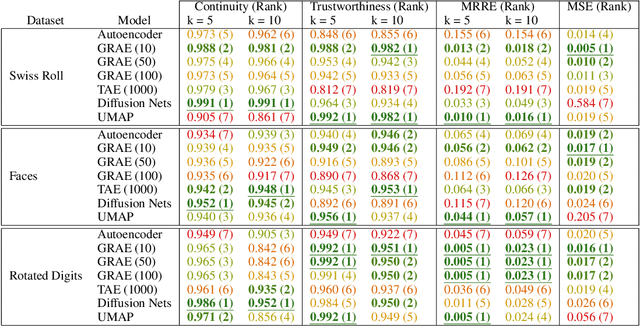
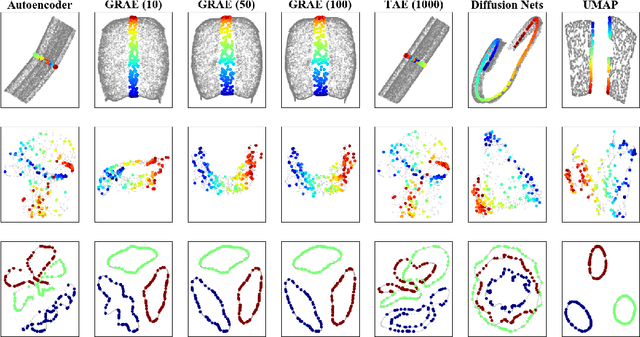
A fundamental task in data exploration is to extract simplified low dimensional representations that capture intrinsic geometry in data, especially for the purpose of faithfully visualizing data in two or three dimensions. Common approaches to this task use kernel methods for manifold learning. However, these methods typically only provide an embedding of fixed input data and cannot extend to new data points. On the other hand, autoencoders have recently become widely popular for representation learning, but while they naturally compute feature extractors that are both extendable to new data and invertible (i.e., reconstructing original features from latent representation), they provide limited capabilities to follow global intrinsic geometry compared to kernel-based manifold learning. Here, we present a new method for integrating both approaches by incorporating a geometric regularization term in the bottleneck of the autoencoder. Our regularization, based on the diffusion potential distances from the recently-proposed PHATE visualization method, encourages the learned latent representation to follow intrinsic data geometry, similar to manifold learning algorithms, while still enabling faithful extension to new data and reconstruction of data in the original feature space from latent coordinates. We compare our approach with leading kernel methods and autoencoder models for manifold learning to provide qualitative and quantitative evidence of our advantages in preserving intrinsic structure, out of sample extension, and reconstruction.

Advantages of biologically-inspired adaptive neural activation in RNNs during learning

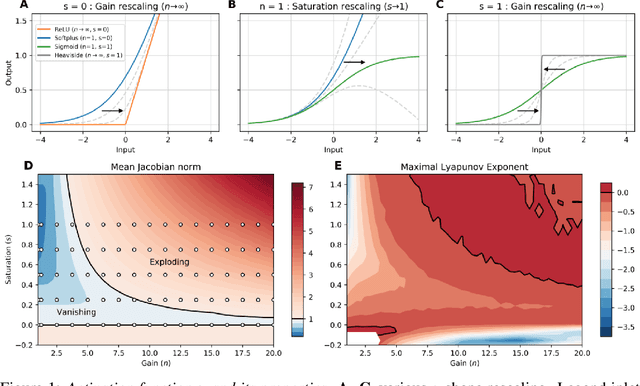
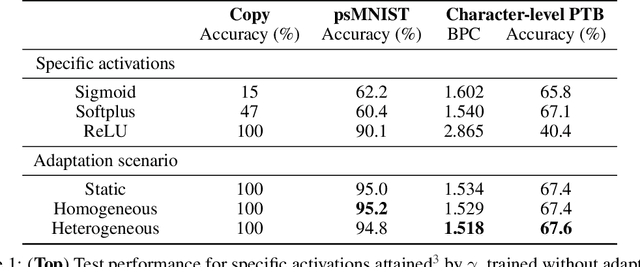
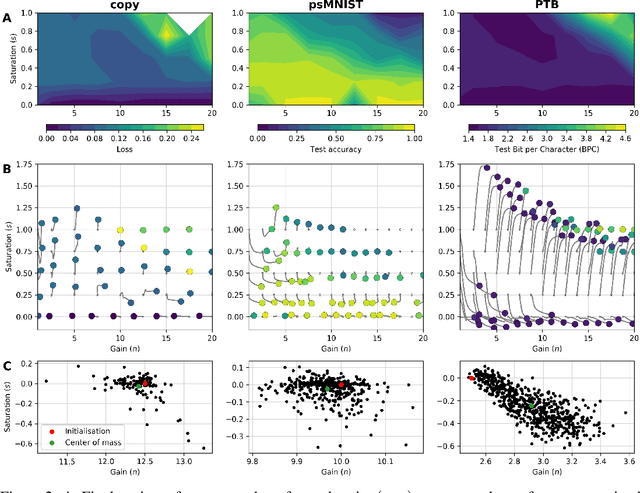
Dynamic adaptation in single-neuron response plays a fundamental role in neural coding in biological neural networks. Yet, most neural activation functions used in artificial networks are fixed and mostly considered as an inconsequential architecture choice. In this paper, we investigate nonlinear activation function adaptation over the large time scale of learning, and outline its impact on sequential processing in recurrent neural networks. We introduce a novel parametric family of nonlinear activation functions, inspired by input-frequency response curves of biological neurons, which allows interpolation between well-known activation functions such as ReLU and sigmoid. Using simple numerical experiments and tools from dynamical systems and information theory, we study the role of neural activation features in learning dynamics. We find that activation adaptation provides distinct task-specific solutions and in some cases, improves both learning speed and performance. Importantly, we find that optimal activation features emerging from our parametric family are considerably different from typical functions used in the literature, suggesting that exploiting the gap between these usual configurations can help learning. Finally, we outline situations where neural activation adaptation alone may help mitigate changes in input statistics in a given task, suggesting mechanisms for transfer learning optimization.

Uncovering the Folding Landscape of RNA Secondary Structure with Deep Graph Embeddings

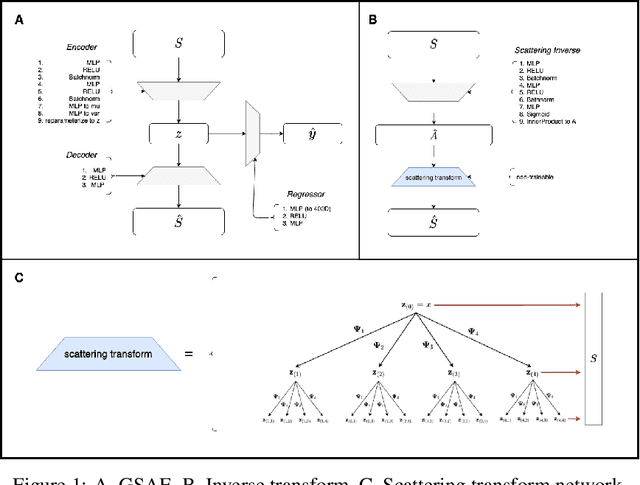
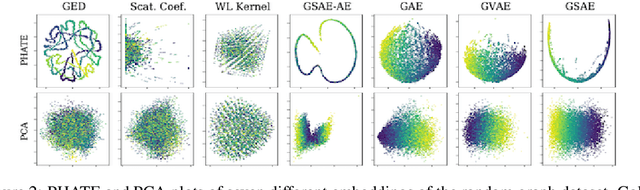
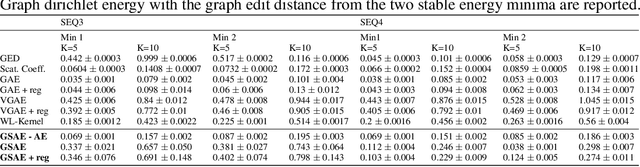
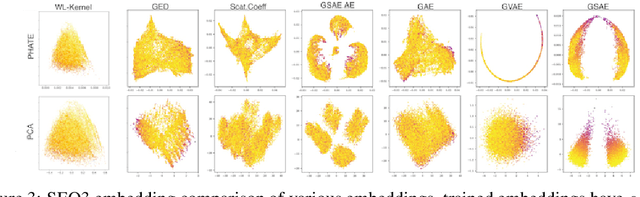
Biomolecular graph analysis has recently gained much attention in the emerging field of geometric deep learning. While numerous approaches aim to train classifiers that accurately predict molecular properties from graphs that encode their structure, an equally important task is to organize biomolecular graphs in ways that expose meaningful relations and variations between them. We propose a geometric scattering autoencoder (GSAE) network for learning such graph embeddings. Our embedding network first extracts rich graph features using the recently proposed geometric scattering transform. Then, it leverages a semi-supervised variational autoencoder to extract a low-dimensional embedding that retains the information in these features that enable prediction of molecular properties as well as characterize graphs. Our approach is based on the intuition that geometric scattering generates multi-resolution features with in-built invariance to deformations, but as they are unsupervised, these features may not be tuned for optimally capturing relevant domain-specific properties. We demonstrate the effectiveness of our approach to data exploration of RNA foldings. Like proteins, RNA molecules can fold to create low energy functional structures such as hairpins, but the landscape of possible folds and fold sequences are not well visualized by existing methods. We show that GSAE organizes RNA graphs both by structure and energy, accurately reflecting bistable RNA structures. Furthermore, it enables interpolation of embedded molecule sequences mimicking folding trajectories. Finally, using an auxiliary inverse-scattering model, we demonstrate our ability to generate synthetic RNA graphs along the trajectory thus providing hypothetical folding sequences for further analysis.

Supervised Visualization for Data Exploration

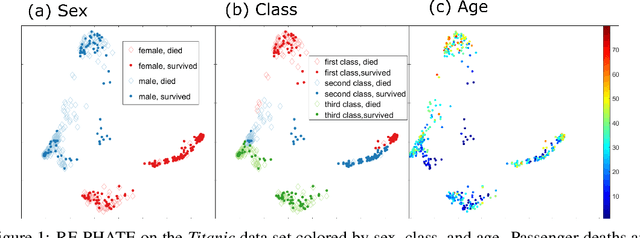
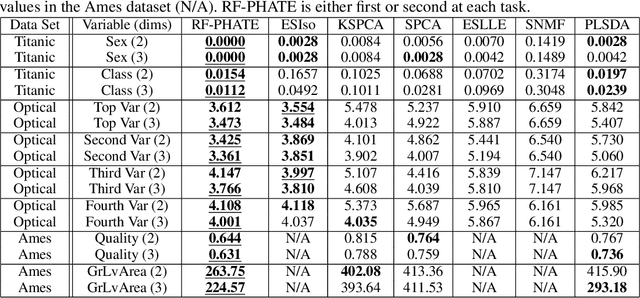
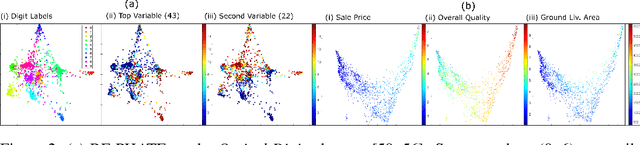
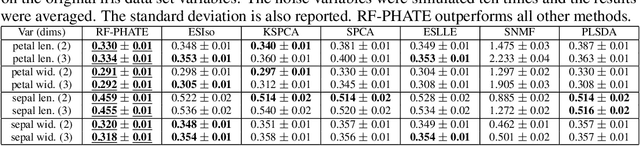
Dimensionality reduction is often used as an initial step in data exploration, either as preprocessing for classification or regression or for visualization. Most dimensionality reduction techniques to date are unsupervised; they do not take class labels into account (e.g., PCA, MDS, t-SNE, Isomap). Such methods require large amounts of data and are often sensitive to noise that may obfuscate important patterns in the data. Various attempts at supervised dimensionality reduction methods that take into account auxiliary annotations (e.g., class labels) have been successfully implemented with goals of increased classification accuracy or improved data visualization. Many of these supervised techniques incorporate labels in the loss function in the form of similarity or dissimilarity matrices, thereby creating over-emphasized separation between class clusters, which does not realistically represent the local and global relationships in the data. In addition, these approaches are often sensitive to parameter tuning, which may be difficult to configure without an explicit quantitative notion of visual superiority. In this paper, we describe a novel supervised visualization technique based on random forest proximities and diffusion-based dimensionality reduction. We show, both qualitatively and quantitatively, the advantages of our approach in retaining local and global structures in data, while emphasizing important variables in the low-dimensional embedding. Importantly, our approach is robust to noise and parameter tuning, thus making it simple to use while producing reliable visualizations for data exploration.

Uncovering the Topology of Time-Varying fMRI Data using Cubical Persistence

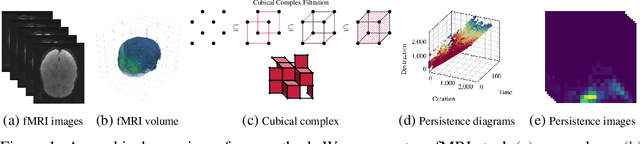
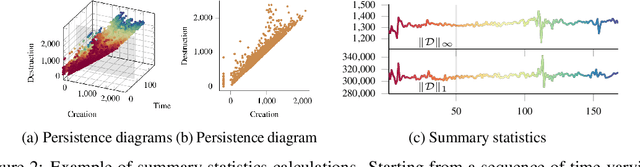
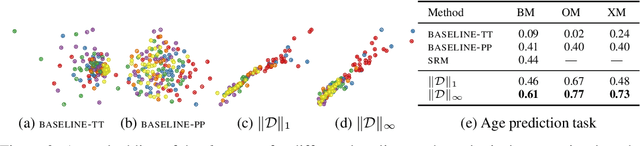
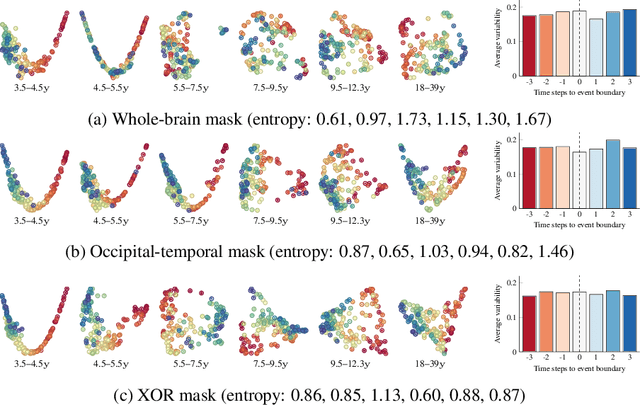
Functional magnetic resonance imaging (fMRI) is a crucial technology for gaining insights into cognitive processes in humans. Data amassed from fMRI measurements result in volumetric data sets that vary over time. However, analysing such data presents a challenge due to the large degree of noise and person-to-person variation in how information is represented in the brain. To address this challenge, we present a novel topological approach that encodes each time point in an fMRI data set as a persistence diagram of topological features, i.e. high-dimensional voids present in the data. This representation naturally does not rely on voxel-by-voxel correspondence and is robust towards noise. We show that these time-varying persistence diagrams can be clustered to find meaningful groupings between participants, and that they are also useful in studying within-subject brain state trajectories of subjects performing a particular task. Here, we apply both clustering and trajectory analysis techniques to a group of participants watching the movie 'Partly Cloudy'. We observe significant differences in both brain state trajectories and overall topological activity between adults and children watching the same movie.

Scattering GCN: Overcoming Oversmoothness in Graph Convolutional Networks

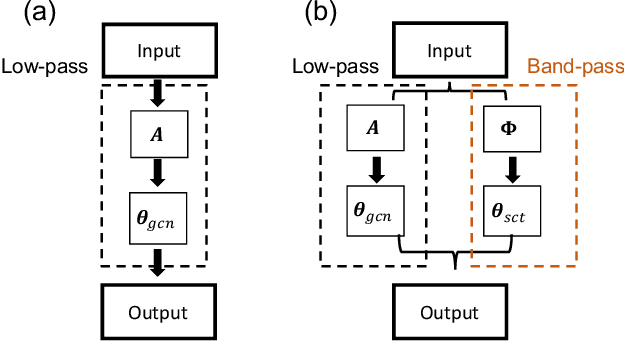
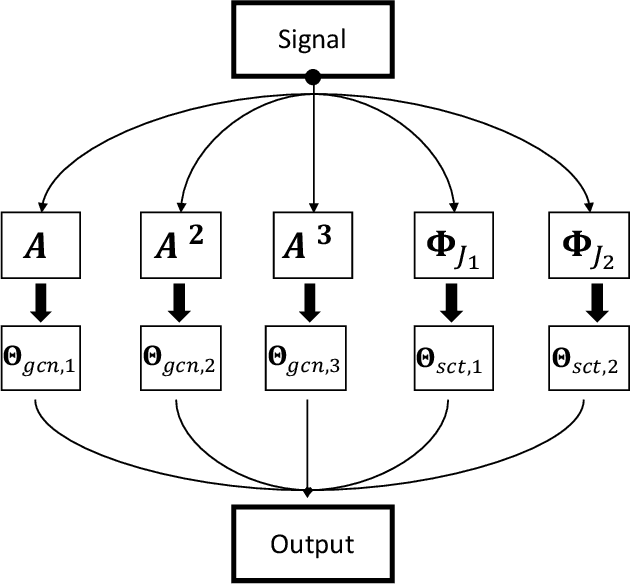
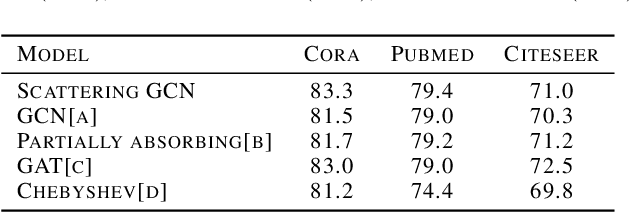
Graph convolutional networks (GCNs) have shown promising results in processing graph data by extracting structure-aware features. This gave rise to extensive work in geometric deep learning, focusing on designing network architectures that ensure neuron activations conform to regularity patterns within the input graph. However, in most cases the graph structure is only accounted for by considering the similarity of activations between adjacent nodes, which in turn degrades the results. In this work, we augment GCN models by incorporating richer notions of regularity by leveraging cascades of band-pass filters, known as geometric scatterings. The produced graph features incorporate multiscale representations of local graph structures, while avoiding overly smooth activations forced by previous architectures. Moreover, inspired by skip connections used in residual networks, we introduce graph residual convolutions that reduce high-frequency noise caused by joining together information at multiple scales. Our hybrid architecture introduces a new model for semi-supervised learning on graph-structured data, and its potential is demonstrated for node classification tasks on multiple graph datasets, where it outperforms leading GCN models.

Identifying Critical Neurons in ANN Architectures using Mixed Integer Programming

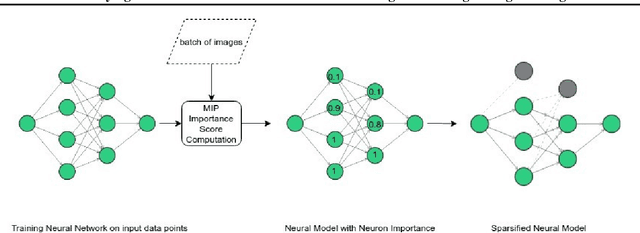
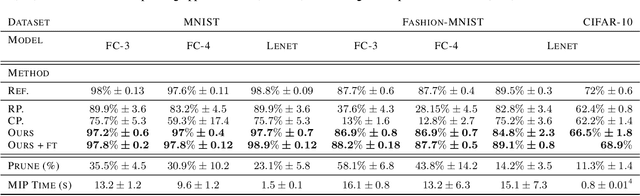
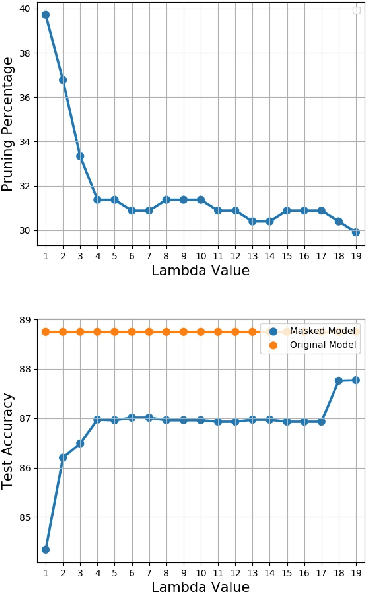
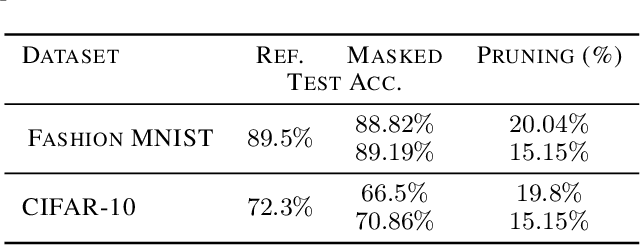
We introduce a novel approach to optimize the architecture of deep neural networks by identifying critical neurons and removing non-critical ones. The proposed approach utilizes a mixed integer programming (MIP) formulation of neural models which includes a continuous importance score computed for each neuron in the network. The optimization in MIP solver minimizes the number of critical neurons (i.e., with high importance score) that need to be kept for maintaining the overall accuracy of the model. Further, the proposed formulation generalizes the recently considered lottery ticket optimization by identifying multiple "lucky" sub-networks resulting in optimized architecture that not only perform well on a single dataset, but also generalize across multiple ones upon retraining of network weights. Finally, the proposed framework provides significant improvement in scalability of automatic sparsification of deep network architectures compared to previous attempts. We validate the performance and generalizability of our approach on MNIST, Fashion-MNIST, and CIFAR-10 datasets, using three different neural networks: LeNet 5 and two ReLU fully connected models.

TrajectoryNet: A Dynamic Optimal Transport Network for Modeling Cellular Dynamics

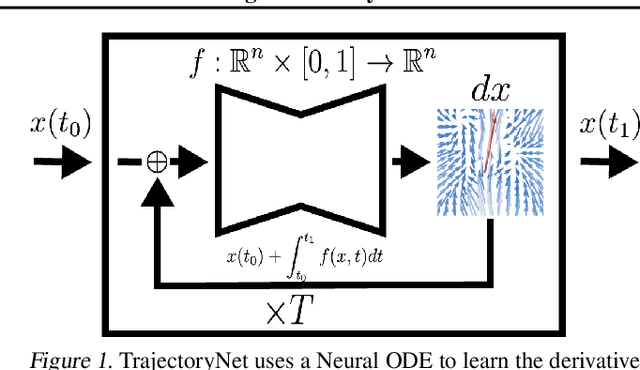
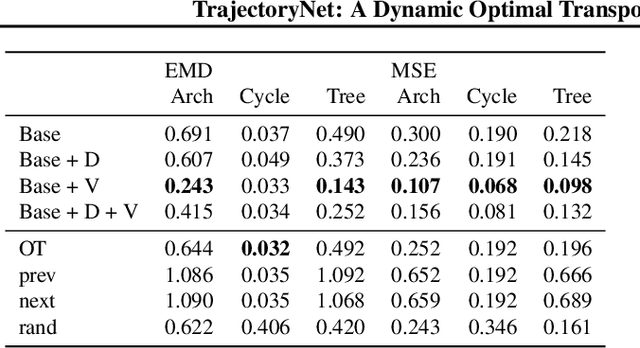
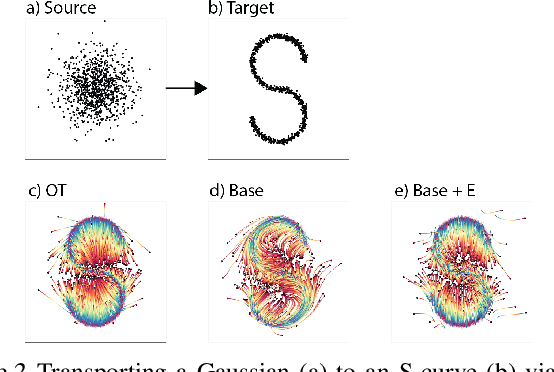
It is increasingly common to encounter data from dynamic processes captured by static cross-sectional measurements over time, particularly in biomedical settings. Recent attempts to model individual trajectories from this data use optimal transport to create pairwise matchings between time points. However, these methods cannot model continuous dynamics and non-linear paths that entities can take in these systems. To address this issue, we establish a link between continuous normalizing flows and dynamic optimal transport, that allows us to model the expected paths of points over time. Continuous normalizing flows are generally under constrained, as they are allowed to take an arbitrary path from the source to the target distribution. We present TrajectoryNet, which controls the continuous paths taken between distributions. We show how this is particularly applicable for studying cellular dynamics in data from single-cell RNA sequencing (scRNA-seq) technologies, and that TrajectoryNet improves upon recently proposed static optimal transport-based models that can be used for interpolating cellular distributions.

Internal representation dynamics and geometry in recurrent neural networks

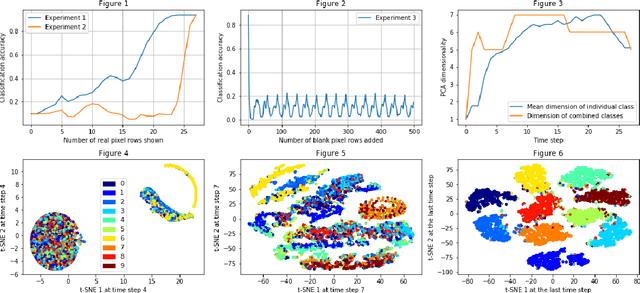
The efficiency of recurrent neural networks (RNNs) in dealing with sequential data has long been established. However, unlike deep, and convolution networks where we can attribute the recognition of a certain feature to every layer, it is unclear what "sub-task" a single recurrent step or layer accomplishes. Our work seeks to shed light onto how a vanilla RNN implements a simple classification task by analysing the dynamics of the network and the geometric properties of its hidden states. We find that early internal representations are evocative of the real labels of the data but this information is not directly accessible to the output layer. Furthermore the network's dynamics and the sequence length are both critical to correct classifications even when there is no additional task relevant information provided.