Convolutional-neural-operator-based transfer learning for solving PDEs

Convolutional neural operator is a CNN-based architecture recently proposed to enforce structure-preserving continuous-discrete equivalence and enable the genuine, alias-free learning of solution operators of PDEs. This neural operator was demonstrated to outperform for certain cases some baseline models such as DeepONet, Fourier neural operator, and Galerkin transformer in terms of surrogate accuracy. The convolutional neural operator, however, seems not to be validated for few-shot learning. We extend the model to few-shot learning scenarios by first pre-training a convolutional neural operator using a source dataset and then adjusting the parameters of the trained neural operator using only a small target dataset. We investigate three strategies for adjusting the parameters of a trained neural operator, including fine-tuning, low-rank adaption, and neuron linear transformation, and find that the neuron linear transformation strategy enjoys the highest surrogate accuracy in solving PDEs such as Kuramoto-Sivashinsky equation, Brusselator diffusion-reaction system, and Navier-Stokes equations.

nPINNs: nonlocal Physics-Informed Neural Networks for a parametrized nonlocal universal Laplacian operator. Algorithms and Applications

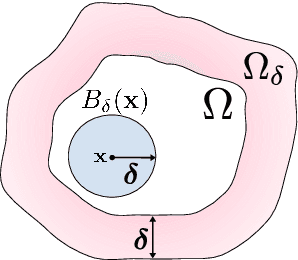
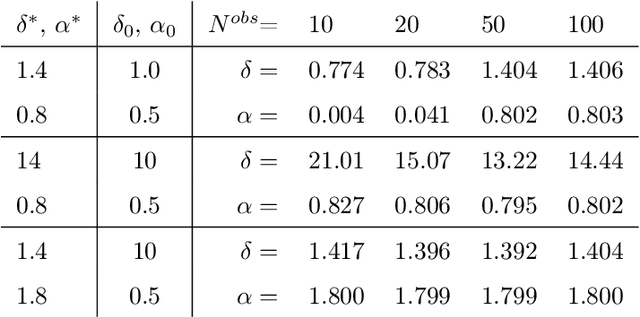
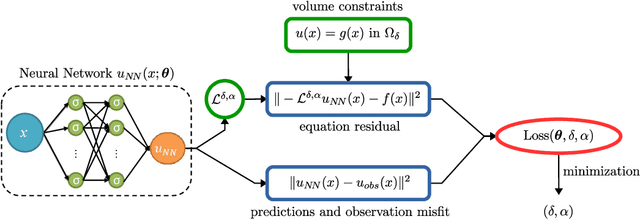
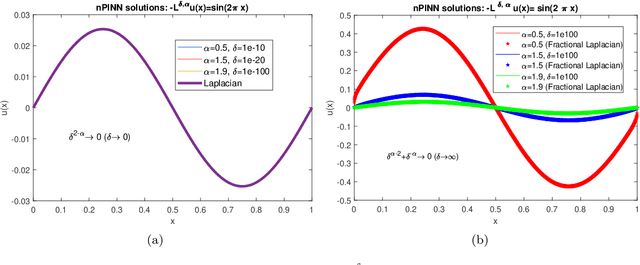
Physics-informed neural networks (PINNs) are effective in solving inverse problems based on differential and integral equations with sparse, noisy, unstructured, and multi-fidelity data. PINNs incorporate all available information into a loss function, thus recasting the original problem into an optimization problem. In this paper, we extend PINNs to parameter and function inference for integral equations such as nonlocal Poisson and nonlocal turbulence models, and we refer to them as nonlocal PINNs (nPINNs). The contribution of the paper is three-fold. First, we propose a unified nonlocal operator, which converges to the classical Laplacian as one of the operator parameters, the nonlocal interaction radius $\delta$ goes to zero, and to the fractional Laplacian as $\delta$ goes to infinity. This universal operator forms a super-set of classical Laplacian and fractional Laplacian operators and, thus, has the potential to fit a broad spectrum of data sets. We provide theoretical convergence rates with respect to $\delta$ and verify them via numerical experiments. Second, we use nPINNs to estimate the two parameters, $\delta$ and $\alpha$. The strong non-convexity of the loss function yielding multiple (good) local minima reveals the occurrence of the operator mimicking phenomenon: different pairs of estimated parameters could produce multiple solutions of comparable accuracy. Third, we propose another nonlocal operator with spatially variable order $\alpha(y)$, which is more suitable for modeling turbulent Couette flow. Our results show that nPINNs can jointly infer this function as well as $\delta$. Also, these parameters exhibit a universal behavior with respect to the Reynolds number, a finding that contributes to our understanding of nonlocal interactions in wall-bounded turbulence.

Neural-net-induced Gaussian process regression for function approximation and PDE solution

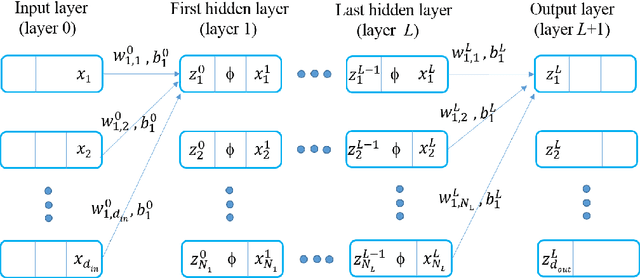
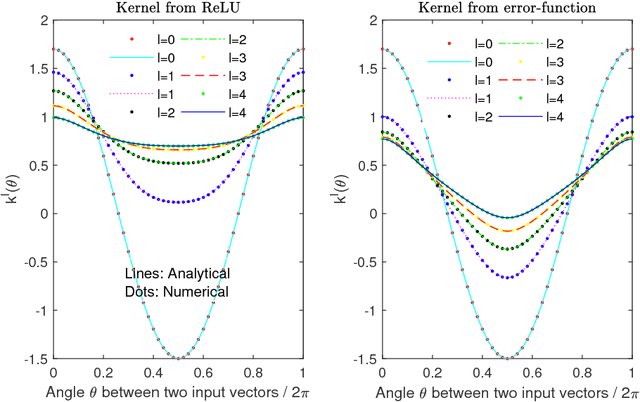
Neural-net-induced Gaussian process (NNGP) regression inherits both the high expressivity of deep neural networks (deep NNs) as well as the uncertainty quantification property of Gaussian processes (GPs). We generalize the current NNGP to first include a larger number of hyperparameters and subsequently train the model by maximum likelihood estimation. Unlike previous works on NNGP that targeted classification, here we apply the generalized NNGP to function approximation and to solving partial differential equations (PDEs). Specifically, we develop an analytical iteration formula to compute the covariance function of GP induced by deep NN with an error-function nonlinearity. We compare the performance of the generalized NNGP for function approximations and PDE solutions with those of GPs and fully-connected NNs. We observe that for smooth functions the generalized NNGP can yield the same order of accuracy with GP, while both NNGP and GP outperform deep NN. For non-smooth functions, the generalized NNGP is superior to GP and comparable or superior to deep NN.