Reciprocal Multi-Robot Collision Avoidance with Asymmetric State Uncertainty

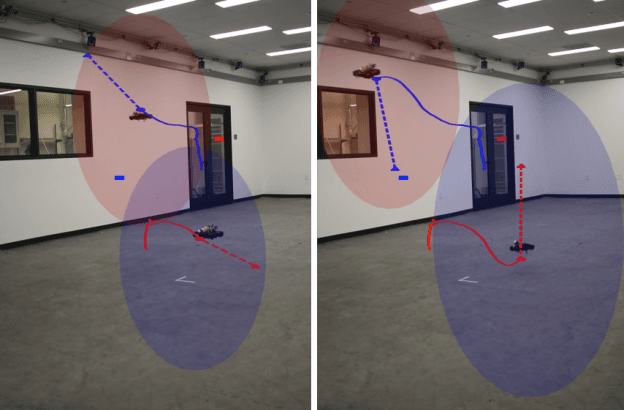
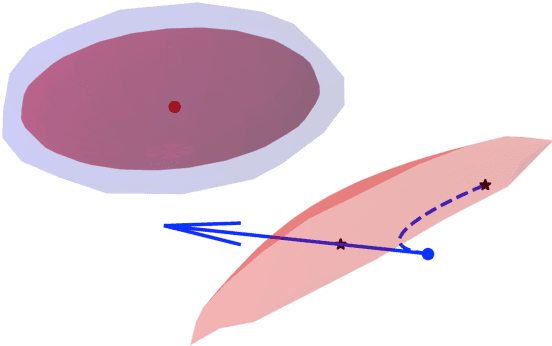
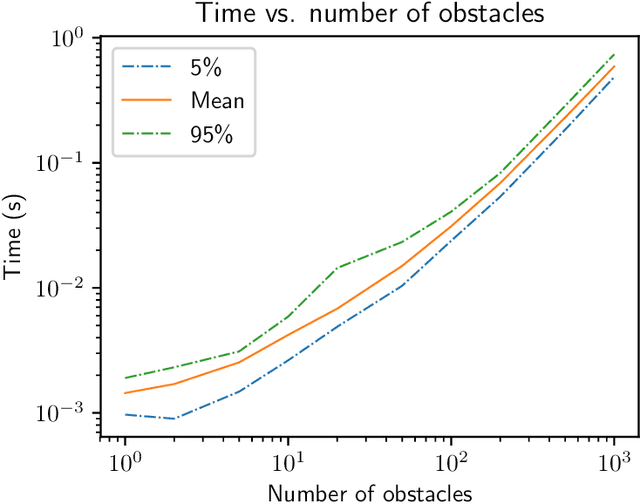
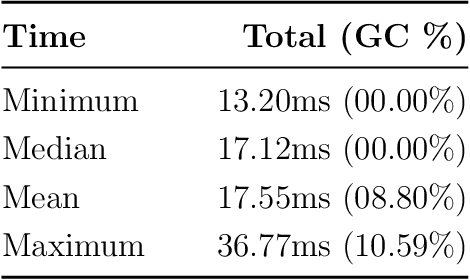
We present a general decentralized formulation for a large class of collision avoidance methods and show that all collision avoidance methods of this form are guaranteed to be collision free. This class includes several existing algorithms in the literature as special cases. We then present a particular instance of this collision avoidance method, CARP (Collision Avoidance by Reciprocal Projections), that is effective even when the estimates of other agents' positions and velocities are noisy. The method's main computational step involves the solution of a small convex optimization problem, which can be quickly solved in practice, even on embedded platforms, making it practical to use on computationally-constrained robots such as quadrotors. This method can be extended to find smooth polynomial trajectories for higher dynamic systems such at quadrotors. We demonstrate this algorithm's performance in simulations and on a team of physical quadrotors. Our method finds optimal projections in a median time of 17.12ms for 285 instances of 100 randomly generated obstacles, and produces safe polynomial trajectories at over 60hz on-board quadrotors. Our paper is accompanied by an open source Julia implementation and ROS package.

Optimal Representative Sample Weighting

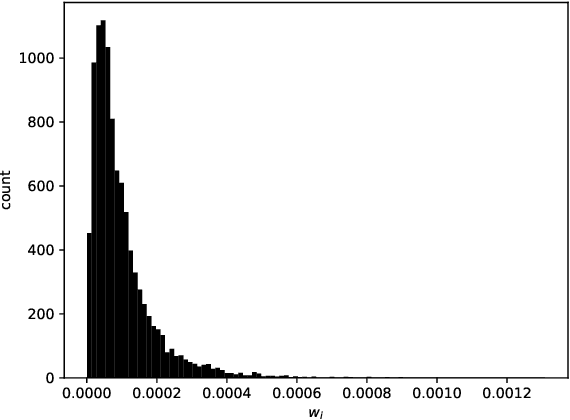
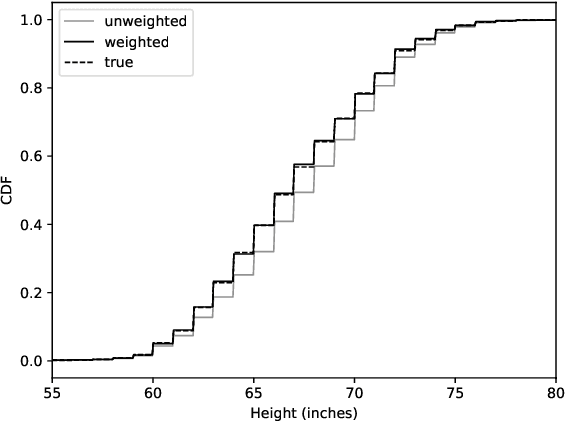
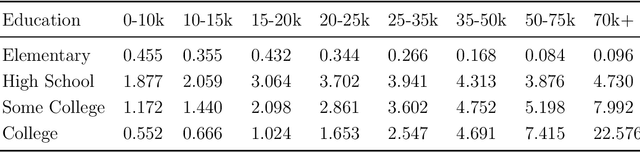
We consider the problem of assigning weights to a set of samples or data records, with the goal of achieving a representative weighting, which happens when certain sample averages of the data are close to prescribed values. We frame the problem of finding representative sample weights as an optimization problem, which in many cases is convex and can be efficiently solved. Our formulation includes as a special case the selection of a fixed number of the samples, with equal weights, i.e., the problem of selecting a smaller representative subset of the samples. While this problem is combinatorial and not convex, heuristic methods based on convex optimization seem to perform very well. We describe rsw, an open-source implementation of the ideas described in this paper, and apply it to a skewed sample of the CDC BRFSS dataset.

Minimizing a Sum of Clipped Convex Functions

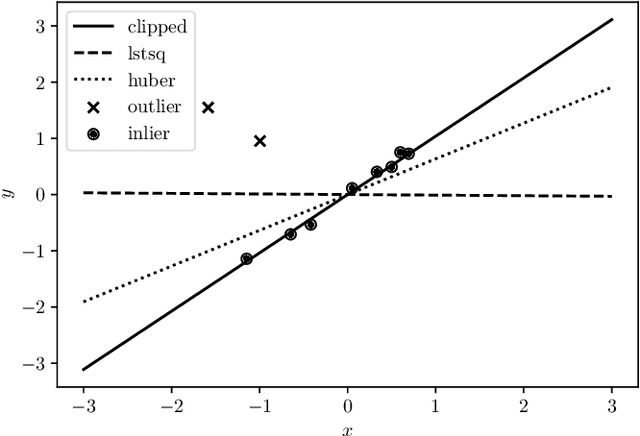
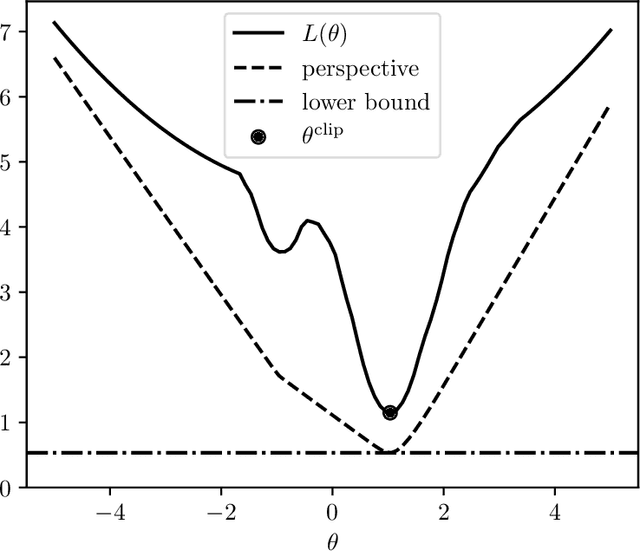
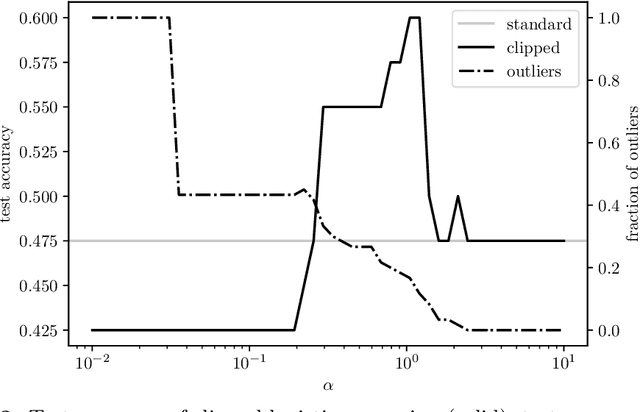
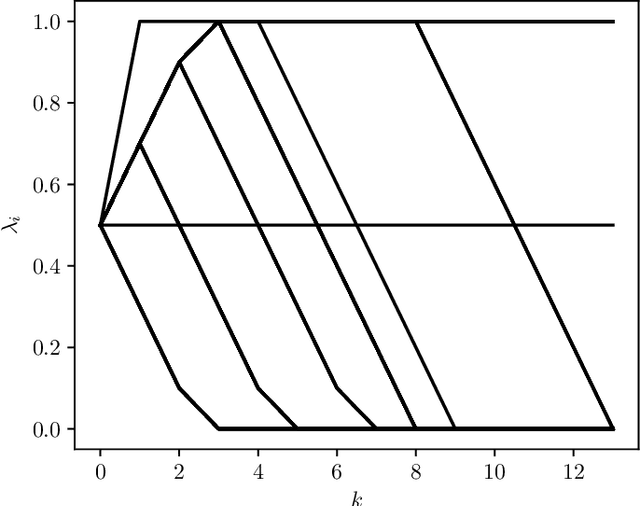
We consider the problem of minimizing a sum of clipped convex functions; applications include clipped empirical risk minimization and clipped control. While the problem of minimizing the sum of clipped convex functions is NP-hard, we present some heuristics for approximately solving instances of these problems. These heuristics can be used to find good, if not global, solutions and appear to work well in practice. We also describe an alternative formulation, based on the perspective transformation, which makes the problem amenable to mixed-integer convex programming and yields computationally tractable lower bounds. We illustrate one of our heuristic methods by applying it to various examples and use the perspective transformation to certify that the solutions are relatively close to the global optimum. This paper is accompanied by an open-source implementation.

Fast Reciprocal Collision Avoidance Under Measurement Uncertainty

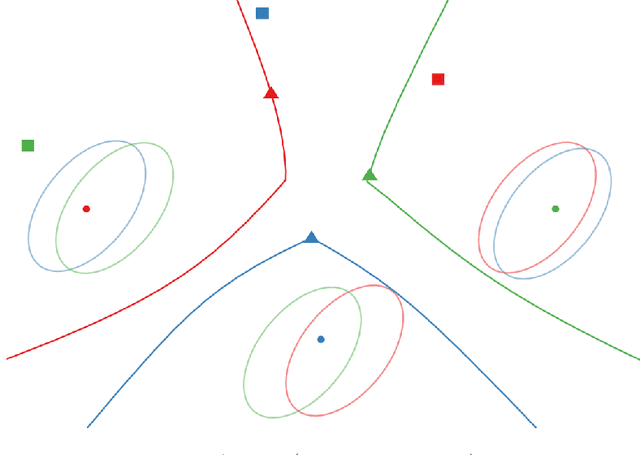
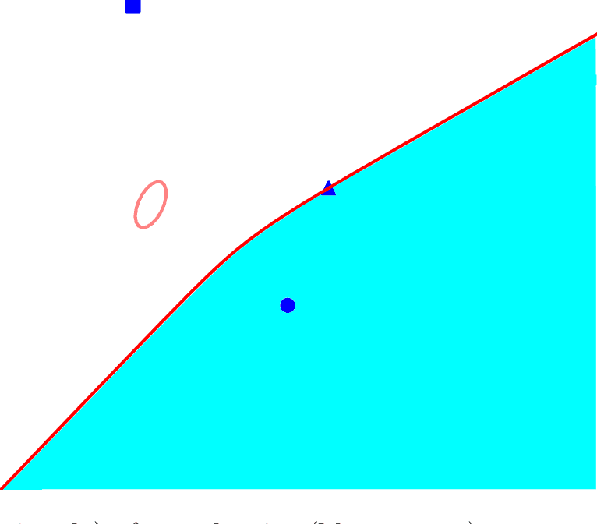
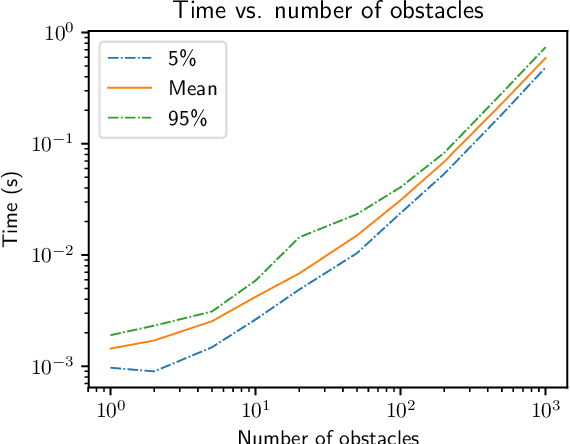
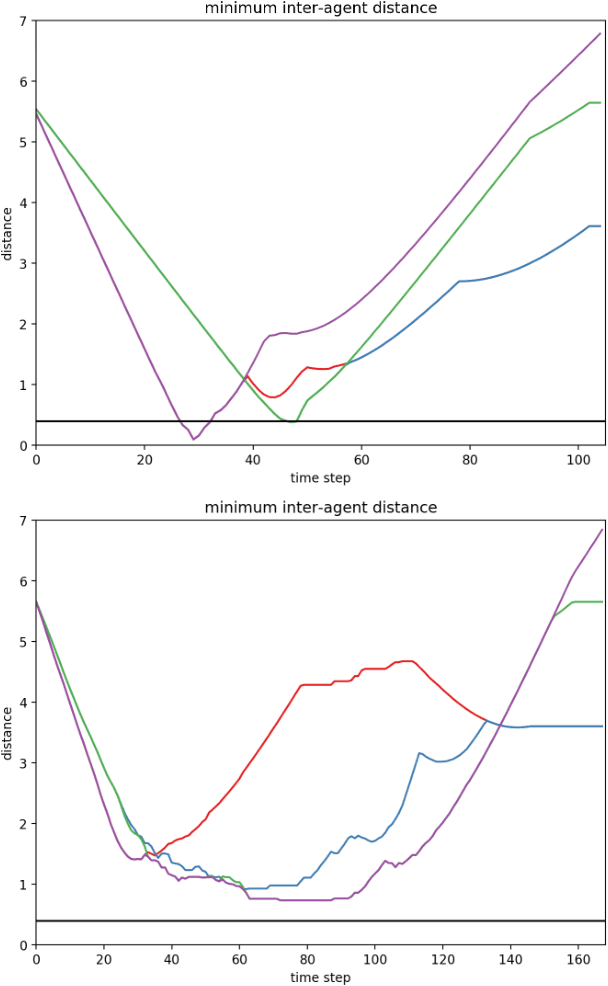
We present a fully distributed collision avoidance algorithm based on convex optimization for a team of mobile robots. This method addresses the practical case in which agents sense each other via measurements from noisy on-board sensors with no inter-agent communication. Under some mild conditions, we provide guarantees on mutual collision avoidance for a broad class of policies including the one presented. Additionally, we provide numerical examples of computational performance and show that, in both 2D and 3D simulations, all agents avoid each other and reach their desired goals in spite of their uncertainty about the locations of other agents.