QSMOTE-PGM/kPGM: QSMOTE Based PGM and kPGM for Imbalanced Dataset Classification

Quantum-inspired machine learning (QiML) leverages mathematical frameworks from quantum theory to enhance classical algorithms, with particular emphasis on inner product structures in high-dimensional feature spaces. Among the prominent approaches, the Kernel Trick, widely used in support vector machines, provides efficient similarity computation, while the Pretty Good Measurement (PGM), originating from quantum state discrimination, enables classification grounded in Hilbert space geometry. Building on recent developments in kernelized PGM (KPGM) and direct PGM-based classifiers, this work presents a unified theoretical and empirical comparison of these paradigms. We analyze their performance across synthetic oversampling scenarios using Quantum SMOTE (QSMOTE) variants. Experimental results show that both PGM and KPGM classifiers consistently outperform a classical random forest baseline, particularly when multiple quantum copies are employed. Notably, PGM with stereo encoding and n_copies=2 achieves the highest overall accuracy (0.8512) and F1-score (0.8234), while KPGM demonstrates competitive and more stable behavior across QSMOTE variants, with top scores of 0.8511 (stereo) and 0.8483 (amplitude). These findings highlight that quantum-inspired classifiers not only provide tangible gains in recall and balanced performance but also offer complementary strengths: PGM benefits from encoding-specific enhancements, whereas KPGM ensures robustness across sampling strategies. Our results advance the understanding of kernel-based and measurement-based QiML methods, offering practical guidance on their applicability under varying data characteristics and computational constraints.

Recognizing Concepts and Recognizing Musical Themes. A Quantum Semantic Analysis

How are abstract concepts and musical themes recognized on the basis of some previous experience? It is interesting to compare the different behaviors of human and of artificial intelligences with respect to this problem. Generally, a human mind that abstracts a concept (say, table) from a given set of known examples creates a table-Gestalt: a kind of vague and out of focus image that does not fully correspond to a particular table with well determined features. A similar situation arises in the case of musical themes. Can the construction of a gestaltic pattern, which is so natural for human minds, be taught to an intelligent machine? This problem can be successfully discussed in the framework of a quantum approach to pattern recognition and to machine learning. The basic idea is replacing classical data sets with quantum data sets, where either objects or musical themes can be formally represented as pieces of quantum information, involving the uncertainties and the ambiguities that characterize the quantum world. In this framework, the intuitive concept of Gestalt can be simulated by the mathematical concept of positive centroid of a given quantum data set. Accordingly, the crucial problem "how can we classify a new object or a new musical theme (we have listened to) on the basis of a previous experience?" can be dealt with in terms of some special quantum similarity-relations. Although recognition procedures are different for human and for artificial intelligences, there is a common method of "facing the problems" that seems to work in both cases.

Pattern recognition on the quantum Bloch sphere

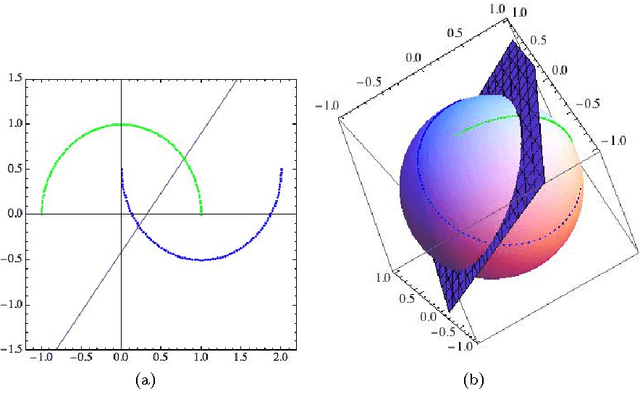
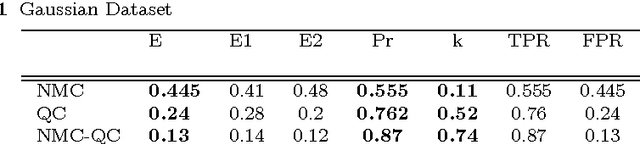
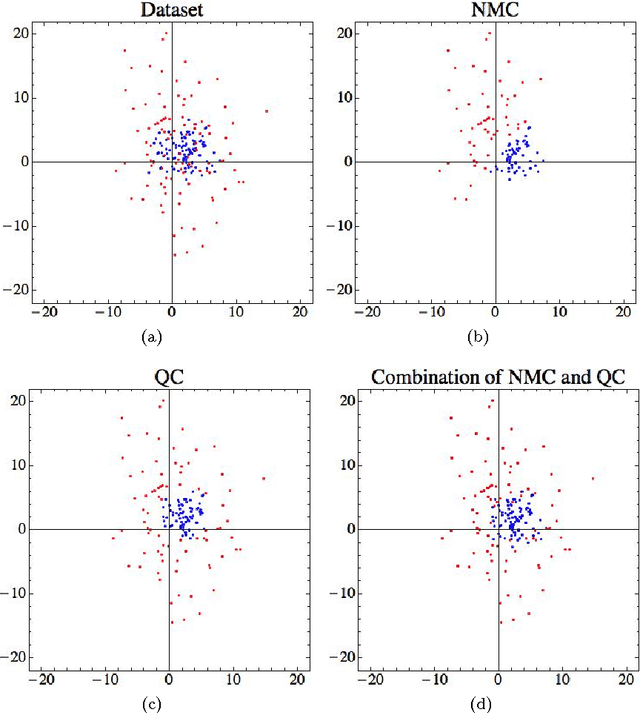
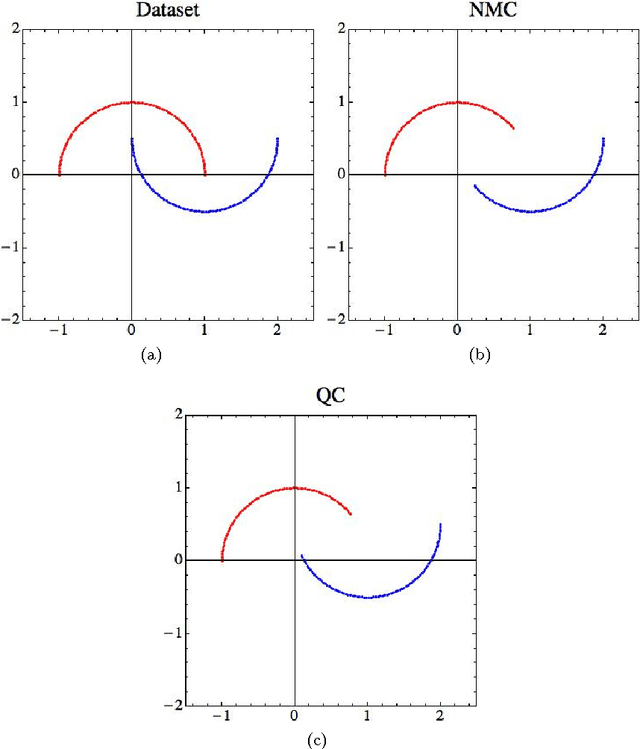
We introduce a framework suitable for describing pattern recognition task using the mathematical language of density matrices. In particular, we provide a one-to-one correspondence between patterns and pure density operators. This correspondence enables us to: i) represent the Nearest Mean Classifier (NMC) in terms of quantum objects, ii) introduce a Quantum Classifier (QC). By comparing the QC with the NMC on different 2D datasets, we show the first classifier can provide additional information that are particularly beneficial on a classical computer with respect to the second classifier.